题目描述

给定一个二叉树，我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。

来源，leetcode 每日一题 968. 监控二叉树

例如：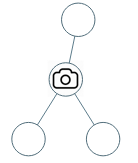
968. 监控二叉树 - 图1

  1. 输入：[0,0,null,0,0]
  2. 输出：1
  3. 解释：如图所示，一台摄像头足以监控所有节点。

注意

  1. 给定树的节点数的范围是 [1, 1000]。

  2. 每个节点的值都是 0。

    解题思路

  3. 从题目中来看，正面攻破比较困难，但是我们可以反过来想，不外乎几种情况，

    1. 如果只有一个节点，那么就只要一个监控就可以
    2. 如果不只有一个节点，那么叶子节点的父节点为监控的策略肯定是更好的
    3. 如果一个节点初次被访问，如果有父节点，则父节点被设为监控节点是一个好的选择。(自底向上遍历)。
  4. 题目中出现的节点类型不外乎两种：监控节点和被监控节点。

  5. 自底向上遍历，逐步设置被监控节点和监控节点，每设置一个监控节点，则其父节点和子节点都会被监控，设为被监控节点。同时可以被更新为监控节点的类型为初次访问节点和被监控节点。

    代码

    1. /**
    2. * Definition for a binary tree node.
    3. * struct TreeNode {
    4. *     int val;
    5. *     TreeNode *left;
    6. *     TreeNode *right;
    7. *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    8. * };
    9. */
    10. class Solution {
    11. public:
    12.  int minCameraCover(TreeNode* root) {
    13.      if (root == NULL) {
    14.          return 0;
    15.      }
    16.      int answer = 0;
    17.      if (root->left != NULL) {
    18.          dfs(root->left, answer, root);
    19.      }
    20.      if (root->right != NULL) {
    21.          dfs(root->right, answer, root);
    22.      }
    23.      if (root->val == 0) {
    24.          answer += 1;
    25.      }
    26.      return answer;
    27.  }
    28.  void dfs(TreeNode* root, int& answer, TreeNode* parent) {
    29.      if (root->left != NULL) {
    30.          dfs(root->left, answer, root);
    31.      }
    32.      if (root->right != NULL) {
    33.          dfs(root->right, answer, root);
    34.      }
    35.      if (root->val == 0) {
    36.          root->val = 2;
    37.          parent->val = 1;
    38.          answer+=1;
    39.      } else if (root->val == 0 && parent->val == 1) {
    40.          root->val = 2;
    41.      } else if (root->val == 1 && parent->val == 0) {
    42.          parent->val = 2;
    43.      }
    45.  }
    46. };