• 困难
  • 中等
  • 简单

    题目描述

    给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

来源，leetcode 每日一题 85. 最大矩形

例如：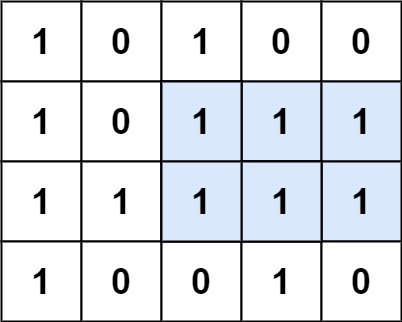
85. 最大矩形 - 图1

  1. 输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
  2. 输出：6
  3. 解释：最大矩形如上图所示。

示例2：

  1. 输入：matrix = []
  2. 输出：0

示例3：

  1. 输入：matrix = [["0","0"]]
  2. 输出：0

解题思路

  1. 暴力方法：最原始地，我们可以列举每个可能的矩形。这可以通过遍历所有的(x1, y1) (x2, y2) 坐标，并以它们为对角顶点来完成。该方法过慢，不足以通过所有测试用例。

  2. 动态规划 - 使用柱状图的优化暴力方法：

    1. 遍历得到每个点的最大宽度85. 最大矩形 - 图2
    2. 计算以每个点为右下角的矩形的最大面积85. 最大矩形 - 图3。
      1. class Solution {
      2. public:
      3. int maximalRectangle(vector<vector<char>>& matrix) {
      4.   int rows = matrix.size();
      5.   if (rows == 0) {
      6.       return 0;
      7.   }
      8.   int columns = matrix[0].size();
      9.   if (columns == 0) {
      10.       return 0;
      11.   }
      12.   vector<vector<int>> maxWidth(rows, vector<int>(columns));
      13.   for (int i = 0; i < rows; i++) {
      14.       if (matrix[i][0] == '1') {
      15.           maxWidth[i][0] = 1;
      16.       }
      17.       for (int j = 1; j < columns; j++) {
      18.           if (matrix[i][j] == '1') {
      19.               maxWidth[i][j] = maxWidth[i][j-1] + 1;
      20.           }
      21.       }
      22.   }
      23.   int max_area = 0;
      24.   for (int j = 0; j < columns; j++) {
      25.       for (int i = 0; i < rows; i++) {
      26.           if (maxWidth[i][j] == 0) {
      27.               continue;
      28.           }
      29.           int height = 1;
      30.           int width = maxWidth[i][j];
      31.           max_area = max(width * height, max_area);
      32.           for (int h = i + 1; h < rows; h++) {
      33.               if (maxWidth[h][j] != 0) {
      34.                   height += 1;
      35.                   width = min(maxWidth[h][j], width);
      36.                   max_area = max(height*width, max_area);
      37.               } else {
      38.                   break;
      39.               }
      40.           }
      41.       }
      42.   }
      43.   return max_area;
      44. }
      45. };

  3. 优化

    1. 求每个点的最大高度

      https://leetcode-cn.com/problems/maximal-rectangle/solution/zui-da-ju-xing-by-leetcode/


    2. 代码

      ```java

class Solution {

  1. public int maximalRectangle(char[][] matrix) {
  2.     if(matrix.length == 0) return 0;
  3.     int m = matrix.length;
  4.     int n = matrix[0].length;
  6.     int[] left = new int[n]; // initialize left as the leftmost boundary possible
  7.     int[] right = new int[n];
  8.     int[] height = new int[n];
  10.     Arrays.fill(right, n); // initialize right as the rightmost boundary possible
  12.     int maxarea = 0;
  13.     for(int i = 0; i < m; i++) {
  14.         int cur_left = 0, cur_right = n;
  15.         // update height
  16.         for(int j = 0; j < n; j++) {
  17.             if(matrix[i][j] == '1') height[j]++;
  18.             else height[j] = 0;
  19.         }
  20.         // update left
  21.         for(int j=0; j<n; j++) {
  22.             if(matrix[i][j]=='1') left[j]=Math.max(left[j],cur_left);
  23.             else {left[j]=0; cur_left=j+1;}
  24.         }
  25.         // update right
  26.         for(int j = n - 1; j >= 0; j--) {
  27.             if(matrix[i][j] == '1') right[j] = Math.min(right[j], cur_right);
  28.             else {right[j] = n; cur_right = j;}    
  29.         }
  30.         // update area
  31.         for(int j = 0; j < n; j++) {
  32.             maxarea = Math.max(maxarea, (right[j] - left[j]) * height[j]);
  33.         }
  34.     return maxarea;
  35. }

} ```