L1W3-neural networks

训练单个样本

一个神经节点（即一个logistic回归单元）：输入x、参数w和b，经过线性计算得到z，z再进行非线性计算（即激活函数）得到输出值a（也就是），接下来就能计算损失函数L。
多层神经网络，就是反复计算每个节点的z和a，最后一个输出值a用来计算loss。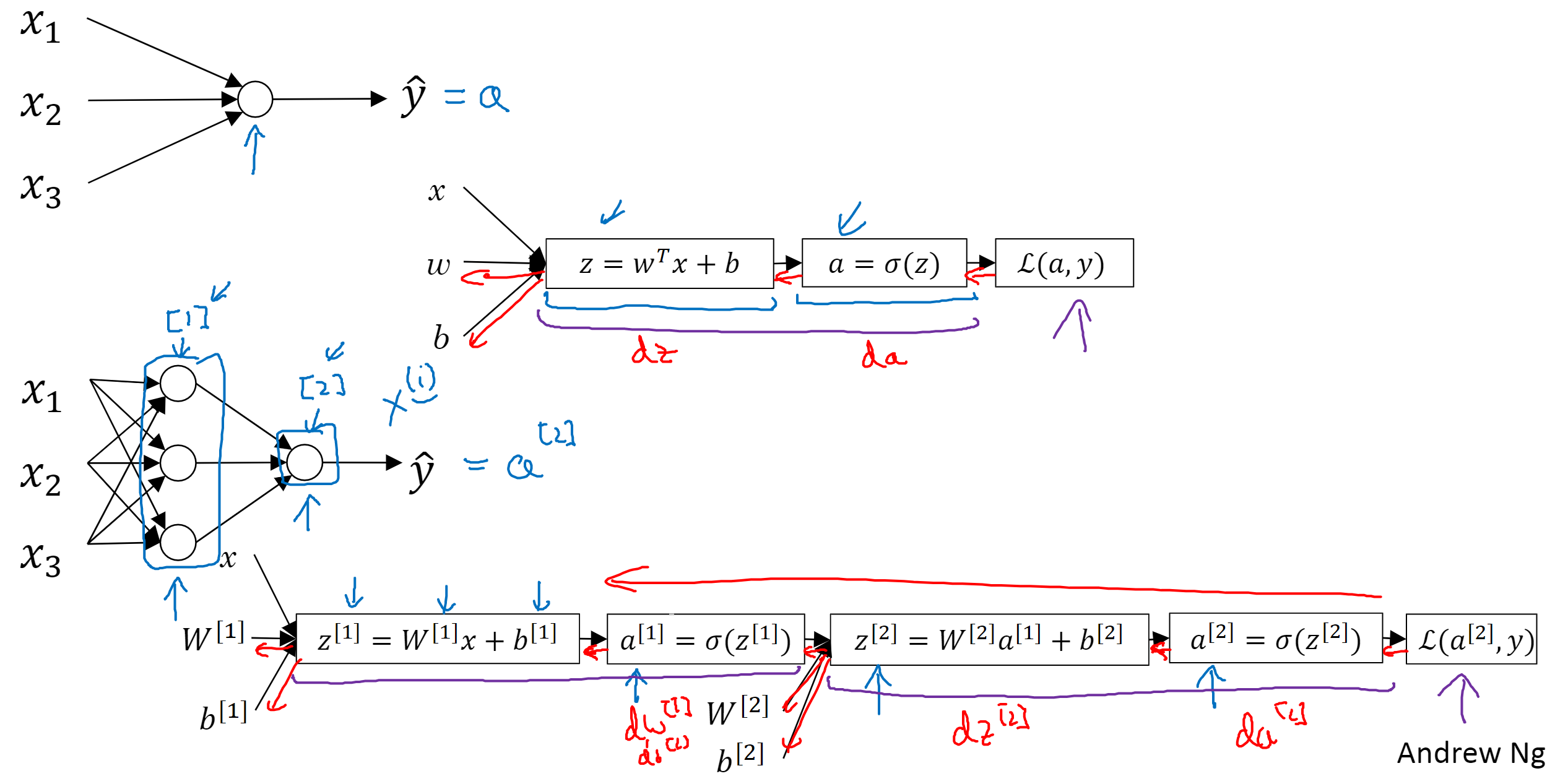

a称为激活值，每一层将a传递给下一层。输入向量X可以表示成。
在计算神经网络的层数时，输入不算在内，输出算。比如上图中下面多神经元的网络，它称为双层神经网络，隐藏层为第一层，输出层为第二层。

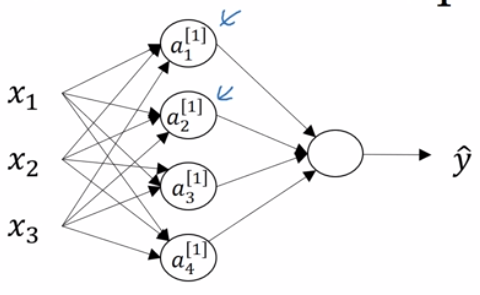
关于维度：
的维度，上标表示第几层，不管。是第一个节点对每个输入的权重，输入有3个，所以是31的向量。 是 的，所以 的维度是 。
速记：W 维度是 当前层节点数 输入节点数，b 维度是 当前层节点数 _ 1。

上式计算向量化：的转置是行向量，把所有堆叠，得到的权重矩阵，b 也同样堆叠成 的列向量，计算得到列向量 Z，激活后得到列向量 a。

多样本向量化

所有操作都一样，多加一个上标，然后向量化、堆叠。上标[i]表示第几层，(j)表示第几个样本。

A和Z的横向指标对应不同的训练样本，竖向指标对应神经网络里的不同节点。

向量化的直观解释：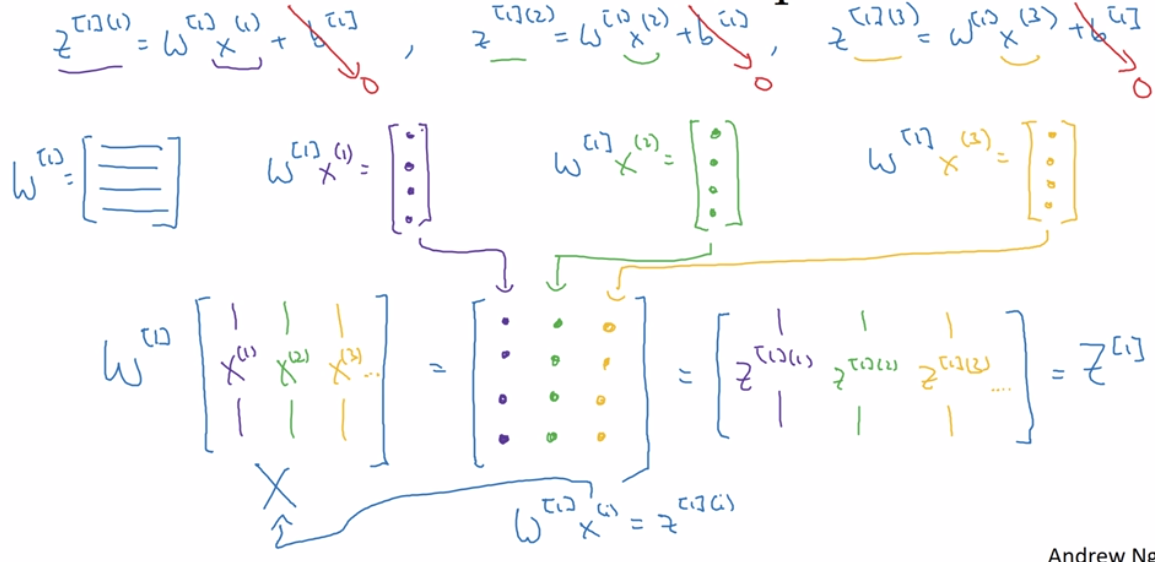

激活函数

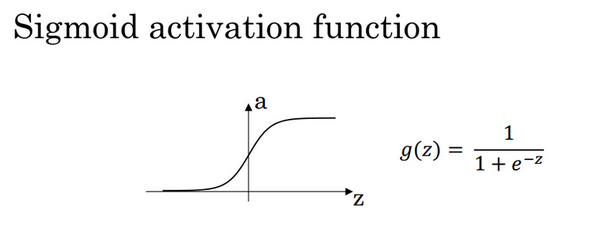
sigmoid 公式：
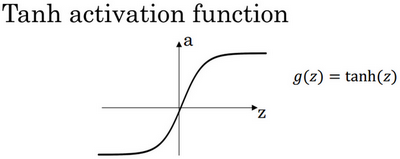
更通常的情况下，使用不同的函数，g可以是除了sigmoid函数以外的非线性函数，tanh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。

tanh 公式：
事实上，tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了(0,0)点，并且值域介于+1和-1之间。这就使得函数的平均值为0，有类似数据中心化的效果。大部分时候tanh更适用，除了输出层，输出层更希望y介于0到1之间。
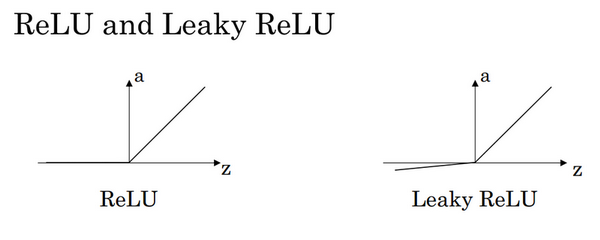
当z非常大或非常小的时候，导数趋近于0，会拖慢梯度下降算法，所以ReLU（修正线性单元）算法十分受欢迎。

ReLU 公式：
它的缺点是，当z为负数时，导数等于0。这时有了Leaky ReLU，使z为负数时有一个很平缓的斜率。不过实际上它的使用率不高，因为神经网络中有足够多的隐藏单元，令z大于0。使用ReLU函数可以使神经网络的学习速度快很多。

这里也有另一个版本的Relu被称为Leaky Relu。
Leaky ReLu 公式：
当z是负值时，这个函数的值不是等于0，而是轻微的倾斜，如图。这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多。为什么常数是0.01？当然，你可以为学习算法选择不同的参数。

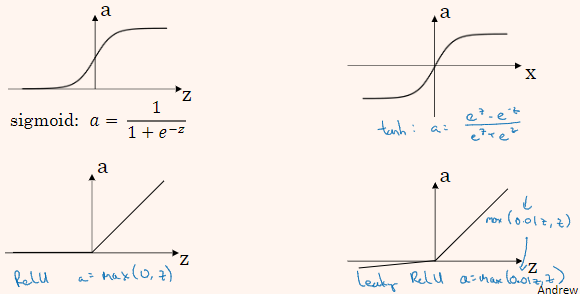
这有一些选择激活函数的经验法则：
如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数。
这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。有时，也会使用tanh激活函数，但Relu的一个优点是：当z是负值的时候，导数等于0。

为什么要使用非线性函数作为激活函数呢？因为线性函数的组合仍然是线性函数，那么无论神经网络有多深，效果都是一样的。
只有机器学习里的回归问题可能用到线性函数作为激活函数。

激活函数的导数

sigmoid

Tanh

ReLU

注：通常在z= 0的时候给定其导数1,0；z=0的情况很少

Leaky ReLU

梯度下降

与上一节介绍的梯度下降不同在于，上一节是单个神经元，这里有一个隐藏层，所以需要多计算一层，但计算公式几乎一样。

注意每个矩阵的维度。

随机初始化

• W不能全部都初始化为0，否则同一层每个神经元经过激活后得到的值相同，反向传播后的计算结果也相同，所有隐藏单元都是对称的。
• b可以全初始化为0，不会有这种对称性。
• 你可以用高斯分布随机初始化权重 np.random.rand((2,2))*0.01。
• 0.01（或其他比较小的值）是为了使权重初始化为很小的随机数，因为在sigmoid函数和tanh函数中，如果权重太大，那么z就会大，使其激活函数的斜率趋近于0，则梯度下降法会非常慢，降低了学习速度。