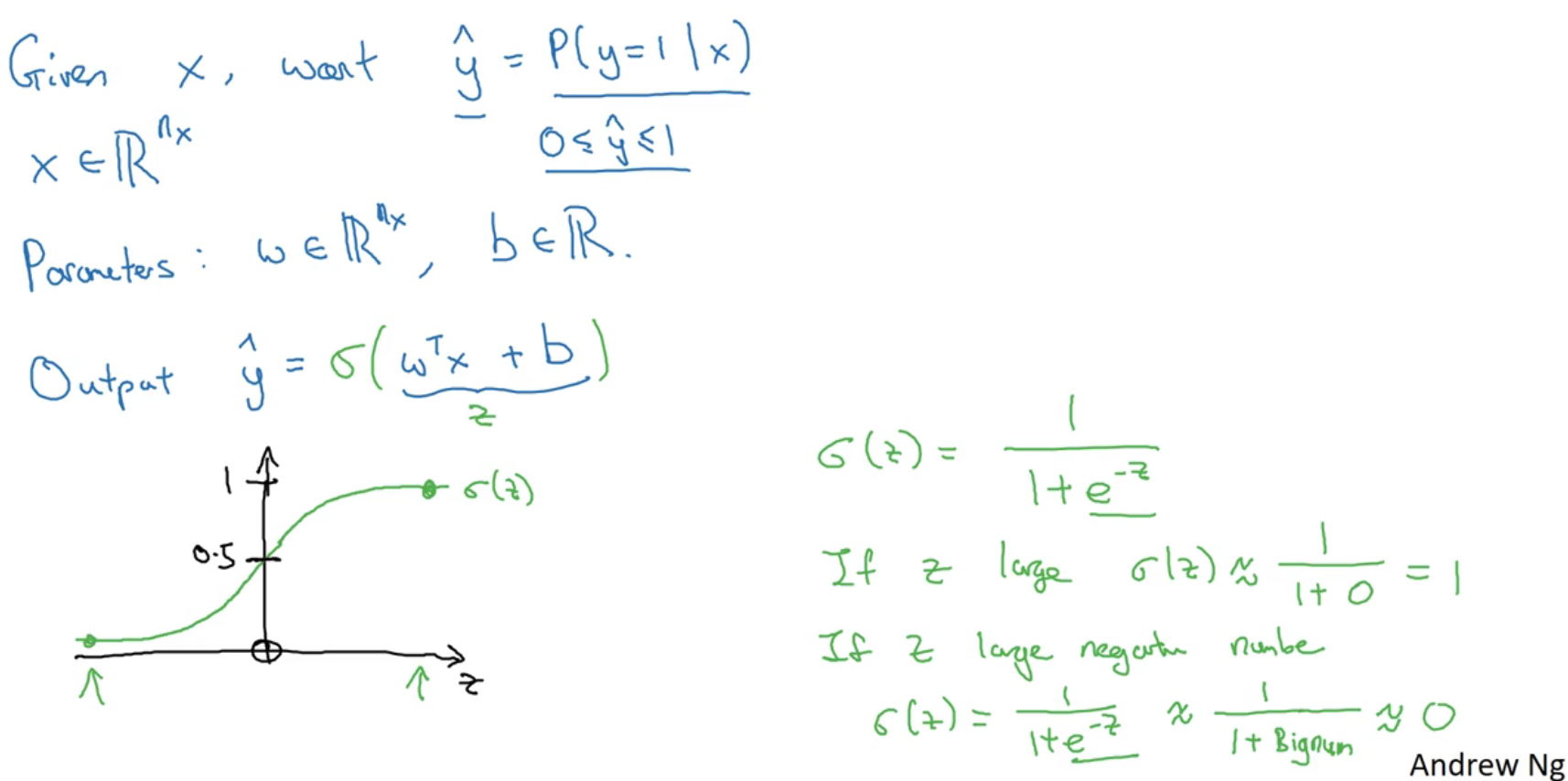主要内容：
符号定义 ：
：表示一个
维数据，为输入数据，维度为
#card=math&code=%28n_x%2C1%29&id=jHbY2)；
：表示输出结果，取值为
#card=math&code=%280%2C1%29&id=Ahb8q)；
%7D%2Cy%5E%7B(i)%7D)#card=math&code=%28x%5E%7B%28i%29%7D%2Cy%5E%7B%28i%29%7D%29&id=NWLVb)：表示第
组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据；
%7D%2Cx%5E%7B(2)%7D%2C…%2Cx%5E%7B(m)%7D%5D#card=math&code=X%3D%5Bx%5E%7B%281%29%7D%2Cx%5E%7B%282%29%7D%2C…%2Cx%5E%7B%28m%29%7D%5D&id=C73iY)：表示所有的训练数据集的输入值，放在一个 
的矩阵中，其中
表示样本数目;
%7D%2Cy%5E%7B(2)%7D%2C…%2Cy%5E%7B(m)%7D%5D#card=math&code=Y%3D%5By%5E%7B%281%29%7D%2Cy%5E%7B%282%29%7D%2C…%2Cy%5E%7B%28m%29%7D%5D&id=DH7Oc)：对应表示所有训练数据集的输出值，维度为
。
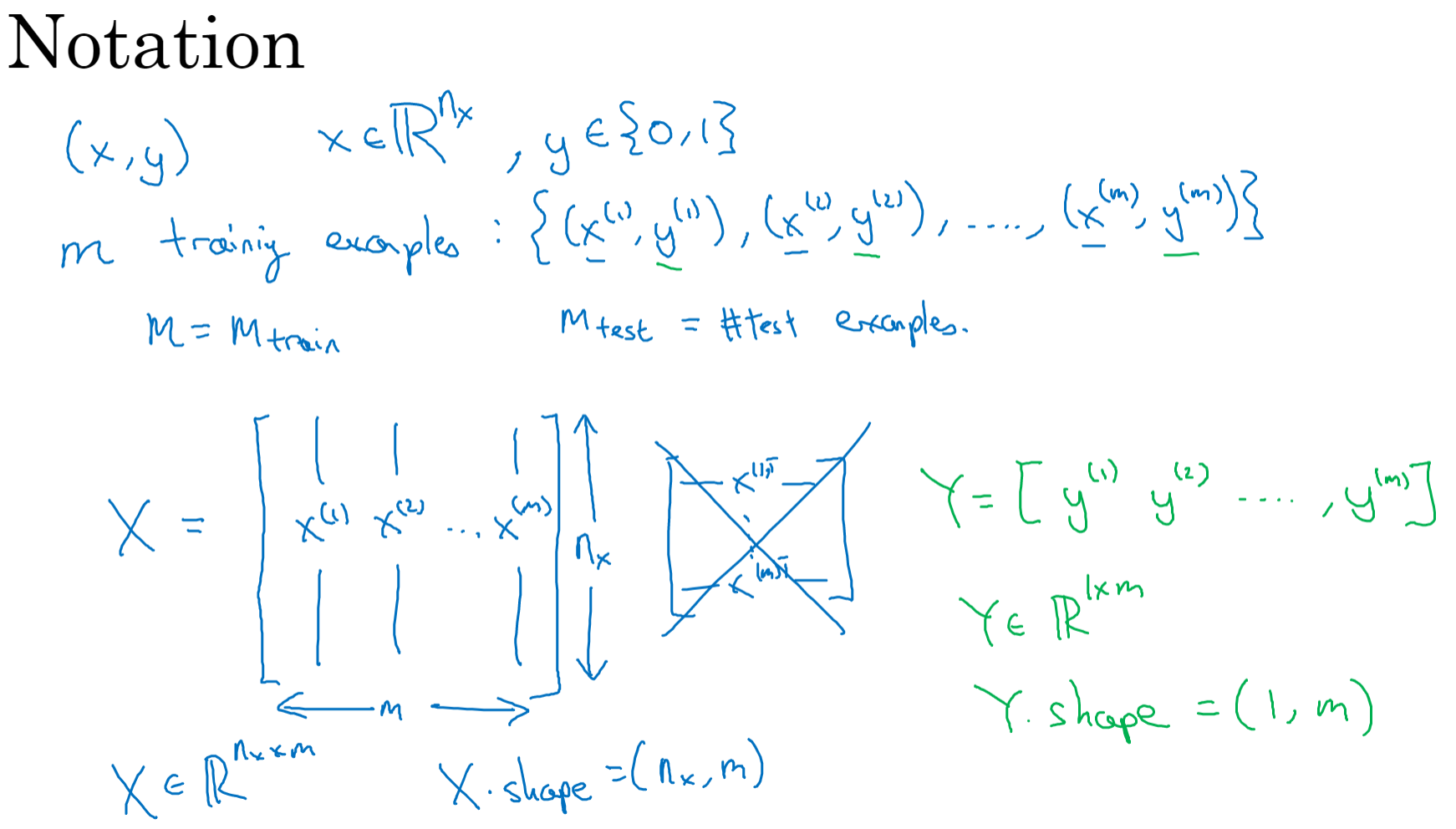
逻辑回归的假设函数 （Hypothesis Function）
是一个
维的向量（相当于有
个特征的特征向量）。
是特征权重，维度与特征向量相同，
是一个实数，表示偏差。- 输入
以及参数
和
之后，我们怎样产生输出预测值
？假设令
，我们想让
表示实际值
等于1的机率的话，
应该在0到1之间。而
可能比1要大得多，或者甚至为一个负值。因此在逻辑回归中，我们的输出应该是
等于由上面得到的线性函数式子作为自变量的sigmoid函数，将线性函数转换为非线性函数。 
#card=math&code=%5Chat%7By%7D%3D%5Csigma%28%7B%7Bw%7D%5E%7BT%7D%7Dx%2Bb%29&id=wx5mO)，
%3D%5Cfrac%7B1%7D%7B1%2B%7B%7Be%7D%5E%7B-z%7D%7D%7D#card=math&code=%5Csigma%20%5Cleft%28%20z%20%5Cright%29%3D%5Cfrac%7B1%7D%7B1%2B%7B%7Be%7D%5E%7B-z%7D%7D%7D&id=dFTv5)，在这里
是一个实数。下图是sigmoid函数的图像，通常都使用
来表示
的值。
逻辑回归的代价函数（Logistic Regression Cost Function）
- 当你实现逻辑回归时，你的工作就是去让机器学习参数
以及
，来得到你想要的输出。 - 损失函数又叫做误差函数，用来衡量预测输出值和实际值有多接近，Loss function:
#card=math&code=L%5Cleft%28%20%5Chat%7By%7D%2Cy%20%5Cright%29&id=zSZ1Y). - 一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值。
- 逻辑回归中用到的损失函数是：%3D-y%5Clog(%5Chat%7By%7D)-(1-y)%5Clog%20(1-%5Chat%7By%7D)#card=math&code=L%5Cleft%28%20%5Chat%7By%7D%2Cy%20%5Cright%29%3D-y%5Clog%28%5Chat%7By%7D%29-%281-y%29%5Clog%20%281-%5Chat%7By%7D%29&id=Wuj8w)
- 当
时损失函数
#card=math&code=L%3D-%5Clog%20%28%5Chat%7By%7D%29&id=lcWvK)，如果想要损失函数
尽可能得小，那么
就要尽可能大。因为sigmoid函数取值
，所以
会无限接近于1。 - 当
时损失函数
#card=math&code=L%3D-%5Clog%20%281-%5Chat%7By%7D%29&id=tLNeO)，如果想要损失函数
尽可能得小，那么
就要尽可能小。因为sigmoid函数取值
，所以
会无限接近于0。
- 上式中损失函数是在单个训练样本中定义的，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对
个样本的损失函数求和然后除以
:
%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%3D1%7D%5E%7Bm%7D%7BL%5Cleft(%20%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B(i)%7D%7D%2C%7B%7By%7D%5E%7B(i)%7D%7D%20%5Cright)%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%3D1%7D%5E%7Bm%7D%7B%5Cleft(%20-%7B%7By%7D%5E%7B(i)%7D%7D%5Clog%20%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B(i)%7D%7D-(1-%7B%7By%7D%5E%7B(i)%7D%7D)%5Clog%20(1-%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B(i)%7D%7D)%20%5Cright)%7D#card=math&code=J%5Cleft%28%20w%2Cb%20%5Cright%29%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%3D1%7D%5E%7Bm%7D%7BL%5Cleft%28%20%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B%28i%29%7D%7D%2C%7B%7By%7D%5E%7B%28i%29%7D%7D%20%5Cright%29%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%3D1%7D%5E%7Bm%7D%7B%5Cleft%28%20-%7B%7By%7D%5E%7B%28i%29%7D%7D%5Clog%20%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B%28i%29%7D%7D-%281-%7B%7By%7D%5E%7B%28i%29%7D%7D%29%5Clog%20%281-%7B%7B%7B%5Chat%7By%7D%7D%7D%5E%7B%28i%29%7D%7D%29%20%5Cright%29%7D&id=zFBMe) - 损失函数只适用于单个训练样本，而代价函数是参数的总代价，我们训练的目标就是找到合适的
和
，来让代价函数 
的总代价降到最低。
logistic 损失函数的解释
- 我们约定
#card=math&code=%5Chat%7By%7D%3Dp%28y%3D1%7Cx%29&id=KmUav) ，即算法的输出
是给定训练样本 
条件下 
等于1的概率。换句话说，如果
，在给定训练样本 
条件下
；反过来说，如果
，在给定训练样本
条件下 
等于1减去
，即
。
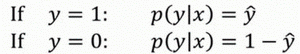
上述的两个条件概率公式可以合并成一个公式：
%3D%7B%5Chat%7By%7D%7D%5E%7By%7D%7B(1-%5Chat%7By%7D)%7D%5E%7B(1-y)%7D%0A#card=math&code=p%28y%7Cx%29%3D%7B%5Chat%7By%7D%7D%5E%7By%7D%7B%281-%5Chat%7By%7D%29%7D%5E%7B%281-y%29%7D%0A&id=oeR5D)
这就是#card=math&code=p%28y%7Cx%29&id=elN8i) 的完整定义。下图是原因解释。
由于 log 函数是严格单调递增的函数，最大化 
)#card=math&code=log%28p%28y%7Cx%29%29&id=LhA7M) 等价于最大化 #card=math&code=p%28y%7Cx%29&id=jhVh7) 并且地计算 #card=math&code=p%28y%7Cx%29&id=rgETe) 的 log对数，也就等于计算
log(1-%5Chat%7By%7D)#card=math&code=ylog%5Chat%7By%7D%2B%281-y%29log%281-%5Chat%7By%7D%29&id=ttVid)
前面提到的损失函数前面有一个负号，因为当你训练学习算法时需要算法输出值的概率是最大的（以最大的概率预测这个值），然而在逻辑回归中我们需要最小化损失函数，因此最小化损失函数与最大化条件概率的对数 )#card=math&code=log%28p%28y%7Cx%29%29&id=BChhk) 关联起来了。
这就是单个训练样本的损失函数表达式。那么，在 
个训练样本的整个训练集中又该如何表示呢？
假设所有的训练样本服从同一分布且相互独立，也即独立同分布的，所有这些样本的联合概率就是每个样本概率的乘积：
%20%3D%20%5Cprod%7Bi%20%3D1%7D%5E%7Bm%7D%7BP(y%5E%7B(i)%7D%7Cx%5E%7B(i)%7D)%7D#card=math&code=P%5Cleft%28%5Ctext%7Blabels%20%20in%20training%20set%7D%20%5Cright%29%20%3D%20%5Cprod%7Bi%20%3D1%7D%5E%7Bm%7D%7BP%28y%5E%7B%28i%29%7D%7Cx%5E%7B%28i%29%7D%29%7D&id=ZRWEp)
在统计学中，最大似然估计（英语：Maximum Likelihood Estimation，简作MLE），也称极大似然估计，是用来估计一个概率模型的参数的一种方法。
给定一个概率分布
，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为
，以及一个分布参数$\theta 
n
X1, X_2,\ldots, X_n
f_D$计算出其似然函数：
%3Df%7B%5Ctheta%20%7D(x%7B1%7D%2C%5Cdots%20%2Cx%7Bn%7D).%7D#card=math&code=%7B%5Cdisplaystyle%20%7B%5Cmbox%7BL%7D%7D%28%5Ctheta%20%5Cmid%20x%7B1%7D%2C%5Cdots%20%2Cx%7Bn%7D%29%3Df%7B%5Ctheta%20%7D%28x%7B1%7D%2C%5Cdots%20%2Cx_%7Bn%7D%29.%7D&id=sfuVJ)
最大化一个似然函数同最大化它的自然对数是等价的。因为自然对数log是一个连续且在似然函数的值域内严格递增的上凹函数。求对数通常能够一定程度上简化运算
最大似然估计 - 维基百科，自由的百科全书
这样我们就推导出了前面给出的logistic回归的成本函数，如下所示。
由于训练模型时，目标是让成本函数最小化，所以我们不是直接用最大似然概率，要去掉这里的负号。最后为了方便，可以对成本函数进行适当的缩放，我们就在前面加一个额外的常数因子
，即:
%3D%20%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%20%3D%201%7D%5E%7Bm%7D%7BL(%5Chat%20y%5E%7B(i)%7D%2Cy%5E%7B(i)%7D)%7D#card=math&code=J%28w%2Cb%29%3D%20%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%20%3D%201%7D%5E%7Bm%7D%7BL%28%5Chat%20y%5E%7B%28i%29%7D%2Cy%5E%7B%28i%29%7D%29%7D&id=azoVo)。
梯度下降
- 初始化
和
，朝最陡的下坡方向走一步，不断地迭代，直到走到全局最优解或者接近全局最优解的地方。这个点就是代价函数（成本函数）#card=math&code=J%28w%2Cb%29&id=ECzNk)这个凸函数的最小值点。
表示学习率（learning rate），用来控制步长（step），即向下走一步的长度
%7D%7Bdw%7D#card=math&code=%5Cfrac%7BdJ%28w%29%7D%7Bdw%7D&id=PWfEI) 就是函数
#card=math&code=J%28w%29&id=f2uJp)对
求导（derivative），在代码中我们会使用
表示这个结果。
表示求偏导符号，可以读作round，小写字母
用在求导数（derivative），即函数只有一个参数，偏导数符号$\partial $ 用在求偏导（partial derivative），即函数含有两个以上的参数。
单个样本的梯度下降
计算图（链式法则）：用
表示
，即 
#card=math&code=%5Chat%7By%7D%3Da%3D%5Csigma%20%28z%29&id=IwbQP)。假设现在只考虑单个样本的情况，单个样本的代价函数定义如下：
%3D-(y%5Clog%20(a)%2B(1-y)%5Clog%20(1-a))#card=math&code=L%28a%2Cy%29%3D-%28y%5Clog%20%28a%29%2B%281-y%29%5Clog%20%281-a%29%29&id=nsSci)，反向计算出代价函数#card=math&code=L%28a%2Cy%29&id=rr1Yd)关于各参数的导数：
%7D%7Bda%7D%3D-y%2Fa%2B(1-y)%2F(1-a)#card=math&code=da%3D%5Cfrac%7BdL%28a%2Cy%29%7D%7Bda%7D%3D-y%2Fa%2B%281-y%29%2F%281-a%29&id=U6acM) ，
#card=math&code=%5Cfrac%7Bda%7D%7Bdz%7D%3Da%5Ccdot%20%281-a%29&id=ftFD5)
%7D%7Bdz%7D%3D%5Cfrac%7BdL%7D%7Bda%7D%5Ccdot%20%5Cfrac%7Bda%7D%7Bdz%7D%3D(%20-%20%5Cfrac%7By%7D%7Ba%7D%20%2B%20%5Cfrac%7B1%20-%20y%7D%7B1%20-%20a%7D)%5Ccdot%20a(1%20-%20a)%20%3D%20a-y#card=math&code=dz%3D%5Cfrac%7BdL%28a%2Cy%29%7D%7Bdz%7D%3D%5Cfrac%7BdL%7D%7Bda%7D%5Ccdot%20%5Cfrac%7Bda%7D%7Bdz%7D%3D%28%20-%20%5Cfrac%7By%7D%7Ba%7D%20%2B%20%5Cfrac%7B1%20-%20y%7D%7B1%20-%20a%7D%29%5Ccdot%20a%281%20-%20a%29%20%3D%20a-y&id=f0cA7)
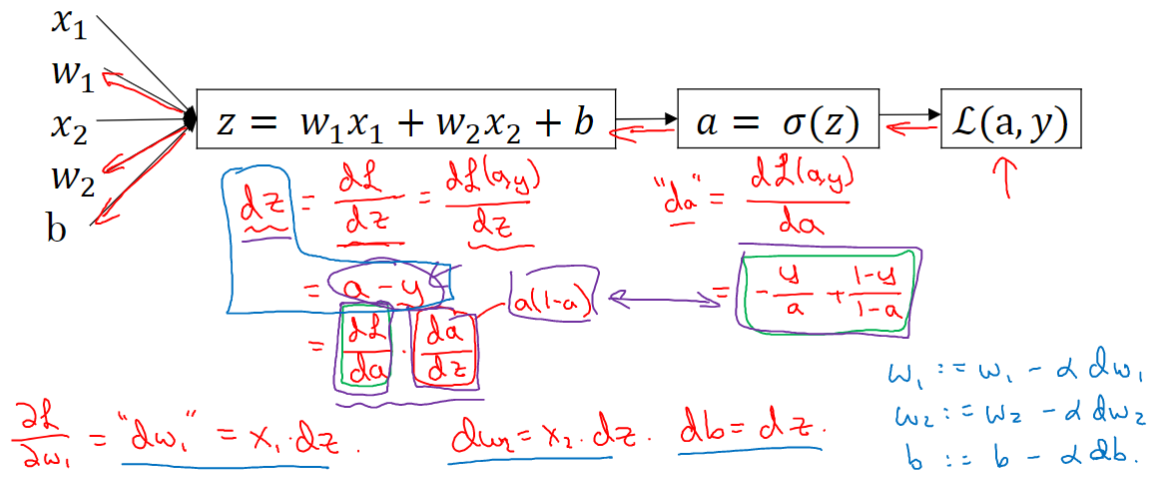
现在进行最后一步反向推导，也就是计算
和
变化对代价函数
的影响，特别地，可以用:
%7D%7D(%7B%7Ba%7D%5E%7B(i)%7D%7D-%7B%7By%7D%5E%7B(i)%7D%7D)#card=math&code=d%7B%7Bw%7D%7B1%7D%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%7D%5E%7Bm%7D%7Bx%7B1%7D%5E%7B%28i%29%7D%7D%28%7B%7Ba%7D%5E%7B%28i%29%7D%7D-%7B%7By%7D%5E%7B%28i%29%7D%7D%29&id=Lbbia)
%7D%7D(%7B%7Ba%7D%5E%7B(i)%7D%7D-%7B%7By%7D%5E%7B(i)%7D%7D)#card=math&code=d%7B%7Bw%7D%7B2%7D%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%7D%5E%7Bm%7D%7Bx%7B2%7D%5E%7B%28i%29%7D%7D%28%7B%7Ba%7D%5E%7B%28i%29%7D%7D-%7B%7By%7D%5E%7B%28i%29%7D%7D%29&id=zv2DC)
%7D%7D-%7B%7By%7D%5E%7B(i)%7D%7D)%7D#card=math&code=db%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Climits%7Bi%7D%5E%7Bm%7D%7B%28%7B%7Ba%7D%5E%7B%28i%29%7D%7D-%7B%7By%7D%5E%7B%28i%29%7D%7D%29%7D&id=VjGkM)
因此，关于单个样本的梯度下降算法，你所需要做的就是如下的事情：
使用公式
#card=math&code=dz%3D%28a-y%29&id=ApTN0)计算
，使用 计算， 计算，
来计算
，然后:
更新，更新，更新
。
m个样本的梯度下降
上一节我们只使用了一个训练样本
%7D%7D%2C%7B%7By%7D%5E%7B(i)%7D%7D)#card=math&code=%28%7B%7Bx%7D%5E%7B%28i%29%7D%7D%2C%7B%7By%7D%5E%7B%28i%29%7D%7D%29&id=T8j64)。 现在你知道全局代价函数，实际上是1到
项各个损失的平均， 所以它表明全局代价函数对
的微分。对
的微分也同样是各项损失对
微分的平均。
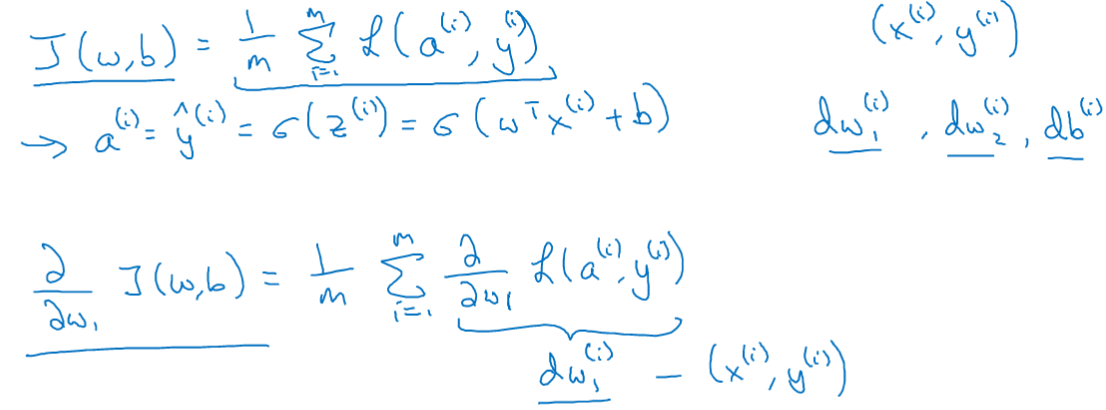
我们把每个样本得出的微分值累加，然后求平均即可。代码流程：
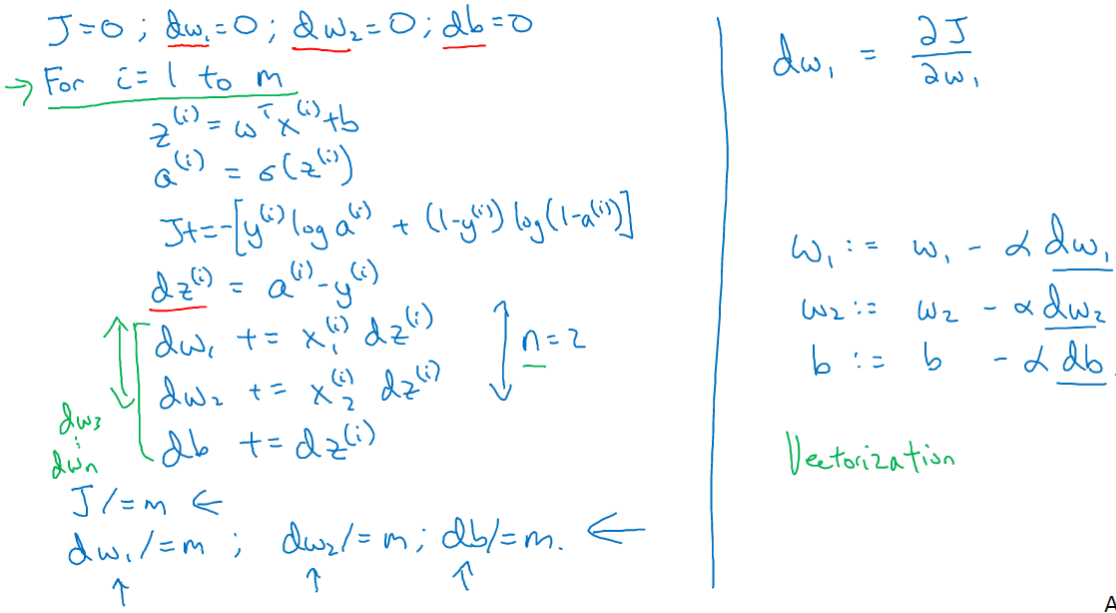
这种计算中有两个缺点，也就是说应用此方法在逻辑回归上你需要编写两个for循环。第一个for循环是一个小循环遍历
个训练样本，第二个for循环是一个遍历所有特征的for循环。向量化可以避开显式的for循环，极大地减少计算时间。
向量化
向量化计算
：z=np.dot(w,x)+b
numpy库有很多向量函数。比如 u=np.log是计算对数函数(
)、 np.abs() 计算数据的绝对值、np.maximum(v, 0) 按元素计算
中每个元素和和0相比的最大值，v**2 代表获得元素 
每个值的平方、 1/v 获取 
中每个元素的倒数等等。所以当你想写循环时候，检查numpy是否存在类似的内置函数，从而避免使用循环(loop)方式。
运用在逻辑回归的梯度下降上，我们想要消除第二循环。我们不用分别初始化 
， 
等于0，而是定义 
为一个向量，设置 
#card=math&code=u%3Dnp.zeros%28n_x%2C1%29&id=NhQBJ)。使 
%7Ddz%5E%7B(i)%7D#card=math&code=dw%2B%3Dx%5E%7B%28i%29%7Ddz%5E%7B%28i%29%7D&id=bDLfv) ，最后令 
。
向量化逻辑回归
前向传播
首先我们回顾一下逻辑回归的前向传播步骤。如果你有 
个训练样本，对第一个样本的计算过程是：计算 
%7D%3Dw%5E%7BT%7Dx%5E%7B(1)%7D%2Bb#card=math&code=z%5E%7B%281%29%7D%3Dw%5E%7BT%7Dx%5E%7B%281%29%7D%2Bb&id=fo4Qj) ，然后计算激活函数 
%7D%3D%5Csigma%20(z%5E%7B(1)%7D)#card=math&code=a%5E%7B%281%29%7D%3D%5Csigma%20%28z%5E%7B%281%29%7D%29&id=SwNN8) ，最后计算得到第一个样本的预测值 
%7D#card=math&code=%5Chat%7By%7D%5E%7B%281%29%7D&id=V6APz) 。对每个样本进行相同的操作。向量化如下图所示：
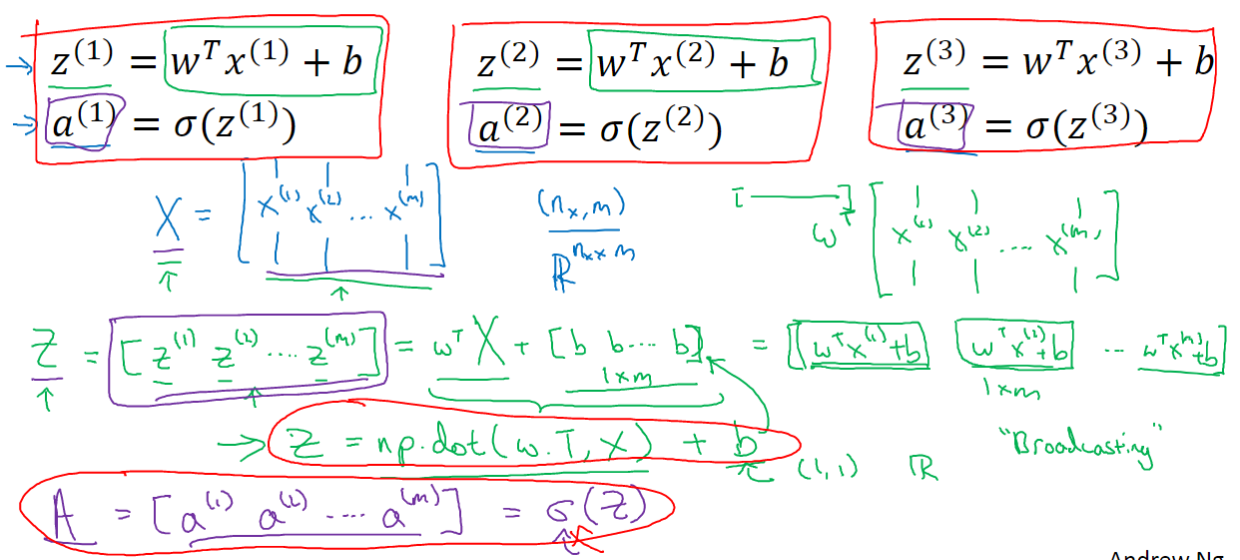
因此可以对 
个训练样本一次性计算出 
和 
：
%2Bb#card=math&code=Z%3Dnp.dot%28w.T%2CX%29%2Bb&id=spcD6)
%7D%20a%5E%7B(2)%7D%20…%20a%5E%7B(m)%7D%5D%3D%5Csigma%20(Z)#card=math&code=A%3D%5Ba%5E%7B%281%29%7D%20a%5E%7B%282%29%7D%20…%20a%5E%7B%28m%29%7D%5D%3D%5Csigma%20%28Z%29&id=LeLfb)
这里在Python中有一个巧妙的地方： 
是一个实数（或者说是一个 
矩阵）。将向量与实数相加时，Python自动把这个实数 
扩展成一个 
的行向量。将常数横向扩展或纵向扩展，这在Python中被称作广播(brosdcasting)。
反向传播
在上一节我们计算得到
，由此
%7D-y%5E%7B(1)%7D%20a%5E%7B(2)%7D-y%5E%7B(2)%7D%20…%20a%5E%7B(m)%7D-y%5E%7B(m)%7D%5D#card=math&code=dZ%3DA-Y%3D%5Ba%5E%7B%281%29%7D-y%5E%7B%281%29%7D%20a%5E%7B%282%29%7D-y%5E%7B%282%29%7D%20…%20a%5E%7B%28m%29%7D-y%5E%7B%28m%29%7D%5D&id=BAIsD)
#card=math&code=db%3D%5Cfrac%7B1%7D%7Bm%7D%2Anp.sum%28dZ%29&id=g0QBz)，
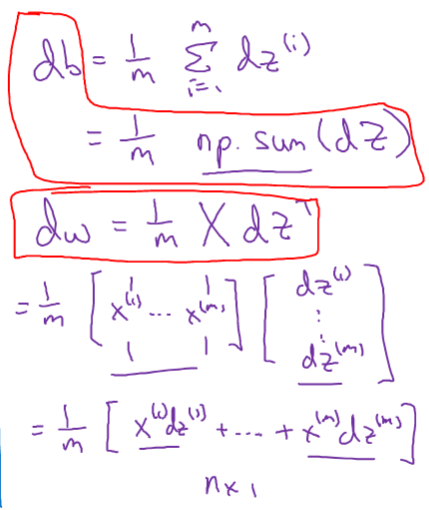
对于一次梯度下降，我们实现了不用for循环对所有训练样本进行预测和求导。
如果你希望多次迭代进行梯度下降，那么仍然需要for循环，例如下图实现的1000次迭代：
python中的broadcasting
我们现在想要计算不同食物中不同营养成分中的卡路里百分比。
下面使用如下代码计算每列的和，可以看到输出是每种食物(100g)的卡路里总和。axis用来指明将要进行的运算是沿着哪个轴执行，在numpy中，0轴是垂直的，也就是列，而1轴是水平的，也就是行。
接下来计算百分比，这条指令将 
的矩阵
除以一个
的矩阵，得到了一个 
的结果矩阵，这个结果矩阵就是我们要求的百分比含量。
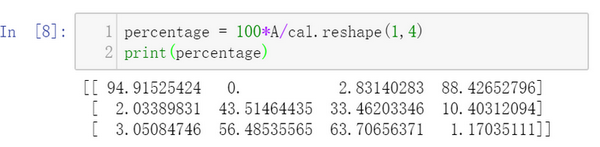
A/cal.reshape(1,4)指令调用了numpy中的广播机制， 
的矩阵
除以
的矩阵
，在计算时
自动向下复制自己，复制到3行。- 其实这里
本身就是
，不需要reshape。 - 重塑操作
reshape是一个常量时间的操作，时间复杂度是
#card=math&code=O%281%29&id=oSLE0)，它的调用代价极低。 - 由于广播巨大的灵活性，有时候你对于广播的特点以及广播的工作原理这些细节不熟悉的话，你可能会产生很细微或者看起来很奇怪的bug。例如，如果你将一个列向量添加到一个行向量中，你会以为它报出维度不匹配或类型错误之类的错误，但是实际上你会得到一个行向量和列向量的求和。
总结一下broadcasting，可以看看下面的图：
关于python numpy向量
为了演示Python-numpy的一个容易被忽略的效果，特别是怎样在Python-numpy中构造向量，让我来做一个快速示范。
首先设置
#card=math&code=a%3Dnp.random.randn%285%29&id=u8nH0)，这样会生成存储在数组 
中的5个高斯随机数变量。之后输出 
，从屏幕上可以得知，此时 
的shape（形状）是一个
#card=math&code=%285%2C%29&id=JnRuM)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量，这也导致它有一些不是很直观的效果。举个例子，如果我输出一个转置阵，最终结果它会和
看起来一样，所以
和
的转置阵最终结果看起来一样。而如果我输出
和
的转置阵的内积，你可能会想：
乘以
的转置返回给你的可能会是一个矩阵。但是如果我这样做，你只会得到一个数。
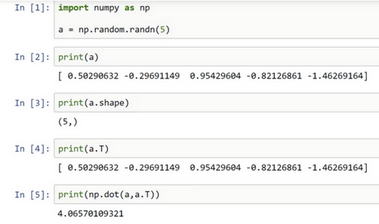
所以建议你编写神经网络时，不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反，如果你设置 
为
#card=math&code=%285%2C1%29&id=sgkLW)，那么这就将置于5行1列向量中。在先前的操作里 
和 
的转置看起来一样，而现在这样的 
变成一个新的 
的转置，并且它是一个行向量。请注意一个细微的差别，在这种数据结构中，当我们输出 
的转置时有两对方括号，而之前只有一对方括号，所以这就是1行5列的矩阵和一维数组的差别。
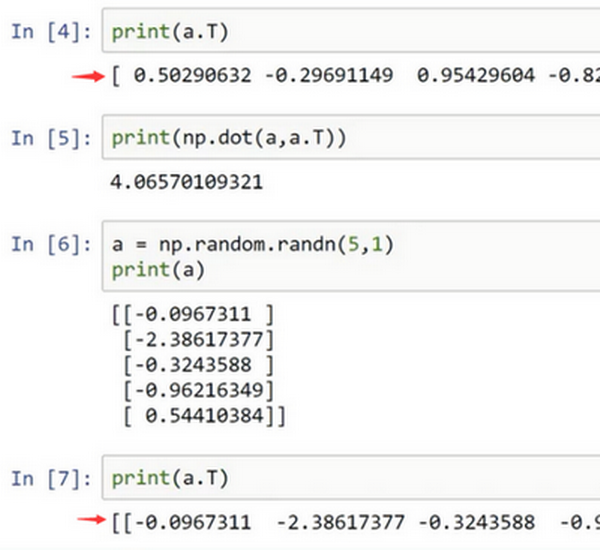
如果你输出 
和 
的转置的乘积，然后会返回给你一个向量的外积，是吧？所以这两个向量的外积返回给你的是一个矩阵。
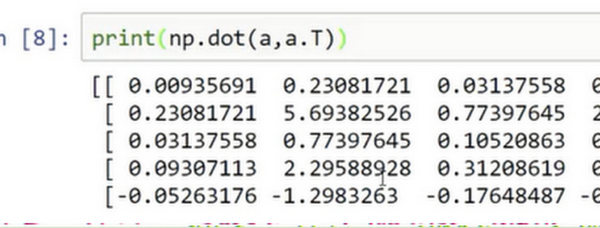
所以我建议，当你在编程练习或者在执行逻辑回归和神经网络时，不要使用#card=math&code=a%3Dnp.random.randn%285%29&id=RRRRk)生成一维数组。而是写明它是行向量还是列向量。
我写代码时还有一件经常做的事，那就是如果我不完全确定一个向量的维度(dimension)，我经常会扔进一个断言语句(assertion statement)。像这样，去确保在这种情况下是一个#card=math&code=%285%2C1%29&id=Lf34U)向量，或者说是一个列向量。这些断言语句实际上是要去执行的，并且它们也会有助于为你的代码提供信息。所以不论你要做什么，不要犹豫直接插入断言语句。如果你不小心以一维数组来执行，你也能够重新改变数组维数 
，表明一个#card=math&code=%285%2C1%29&id=DGU3e)数组或者一个
#card=math&code=%281%2C5%29&id=kXDJH)数组，以致于它表现更像列向量或行向量。
总是使用 
维矩阵（基本上是列向量），或者 
维矩阵（基本上是行向量），这样你可以减少很多assert语句来节省审核矩阵和数组的维数的时间。另外，为了确保你的矩阵或向量所需要的维数时，不要羞于 reshape 操作。
总之，我希望这些建议能帮助你解决一个Python中的bug，从而使你更容易地完成练习。
