一、数学向量

定理: 如果两个向量a、b不共线，那么向量p与向量a、b共面的充要条件是：存在唯一实数对x、y，使p=xa+yb
**
在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i、j作为基底,a为坐标平面内的任意向量,以坐标原点O为起点作向量OP = a.
根据定理可知,有且只有一对实数x、y,使得 向量OP = xi + yj, 即 a = xi + yj
因为 i、j为x、y轴的单位向量, 则实数(x、y)即为向量的坐标, p点的坐标就是(x, y).向量OP称为点p的位置向量

二、canvas画图中的直线旋转

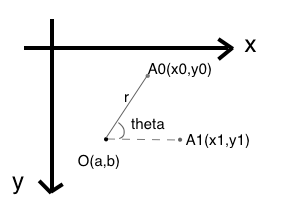
image.png
如上图，以O点(a,b)为圆心，r为半径，A0点（坐标已知）旋转theta角度到A1，怎样获取A1的坐标?

利用向量的方法:
image.png
坐标单位矢量e1,e2（单位为1，方向分别代表x、y轴，实际上e头上应该还有个箭头）

如果e1以原点为圆心顺时针旋转theta后，得到坐标如上图所示e1(cos theta) + e2 (sin theta)，也即坐标为（cos theta , sin theta）单位长度为1

e2顺时针旋转旋转后的坐标为 e1(-sin theta)+e2 (cos theta)，也即（-sin theta , cos theta）旋转后在x轴的负方向

某点的坐标为(x,y)可以拆解为xe1 + y_e2，绕着原点旋转后即:
x(e1(cos theta) + e2 (sin theta) ) + y ( e1(-sin theta) + e2 (cos theta) )
化简: e1(x(_cos theta)-y(sin theta)) + e2*(x(sin theta) + y(_cos theta)_)

所以 某坐标(x,y)绕 原点旋转一定的角度后的坐标为 ((x(cos theta)-y(sin theta)), x(sin theta) + y(_cos theta)_)

image.png