Part 2-2 梯度

假设函数，我们有一种方法来衡量它与数据的拟合程度。 现在我们需要估计假设函数中的参数和。想象一下，我们根据和绘制我们的假设函数（实际上我们将代价函数绘制为参数估计的函数）。 我们不是在绘制 x 和 y 本身，而是绘制我们假设函数的参数范围以及选择一组特定参数所产生的代价。
我们在 x 轴上放置和 y 轴上放置，代价函数在垂直 z 轴上。 我们图表上的点将是代价函数的结果，使用我们的假设和那些特定的 theta 参数。 下图描述了这样的设置。

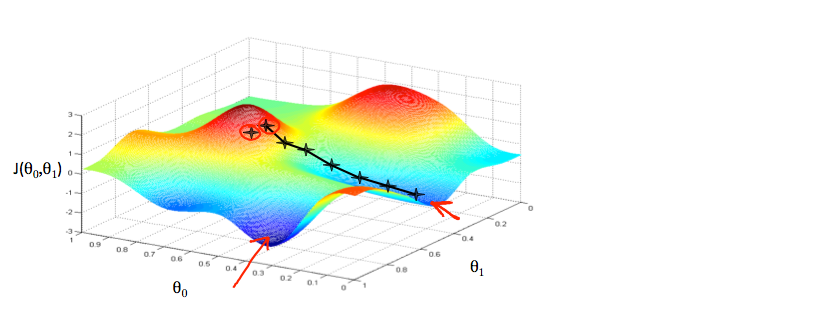
当我们的代价函数位于图中坑的最底部时，即当它的值是最小值时，我们就会知道我们已经成功了。 红色箭头显示图中的最小点。我们这样做的方法是取我们的代价函数的导数（函数的切线）。 切线的斜率是该点的导数，它将为我们提供前进的方向。 我们在下降最陡的方向上降低代价函数。 每一步的大小由参数α决定，称为学习率。例如，上图中每个“星星”之间的距离表示由我们的参数 α 确定的步骤。 较小的 α 会导致较小的步长，而较大的 α 会导致较大的步长。 采取步骤的方向由 的偏导数确定。 根据一个人在图表上的开始位置，一个人可能会在不同的点结束。 上图向我们展示了两个不同的起点，它们在两个不同的地方结束。
梯度下降算法为：
重复直到收敛：
这个式子的含义是将右边的值赋给左边

和要同步更新，如上图左边部分所示

假设函数：
代价函数：
偏导数：

在本视频中，我们探讨了使用一个参数并绘制其成本函数以实现梯度下降的场景。 我们的单个参数公式是：
重复直到收敛：

无论斜率的符号如何，最终都会收敛到其最小值。 下图显示，当斜率为负时， 的值增加，当斜率为正时， 的值减少。

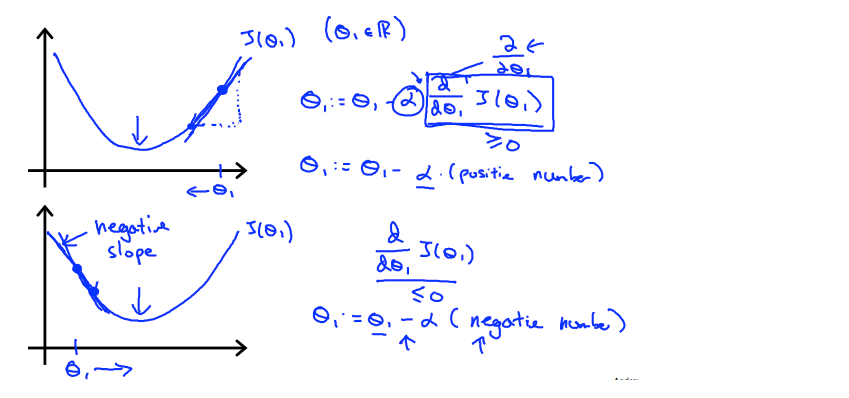
另外，我们应该调整我们的参数 α 以确保梯度下降算法在合理的时间内收敛。 未能收敛或获得最小值的时间过长意味着我们的步长是错误的。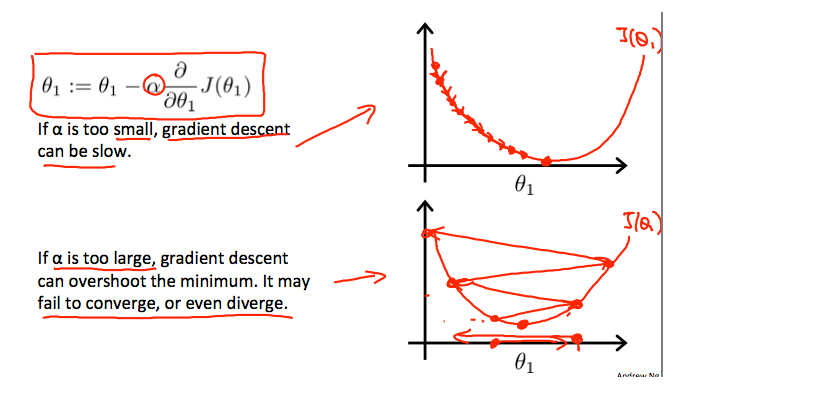

梯度下降如何以固定步长 α 收敛？
收敛背后的直觉是当我们接近凸函数的底部时接近 0。 至少，导数将始终为 0，因此我们得到：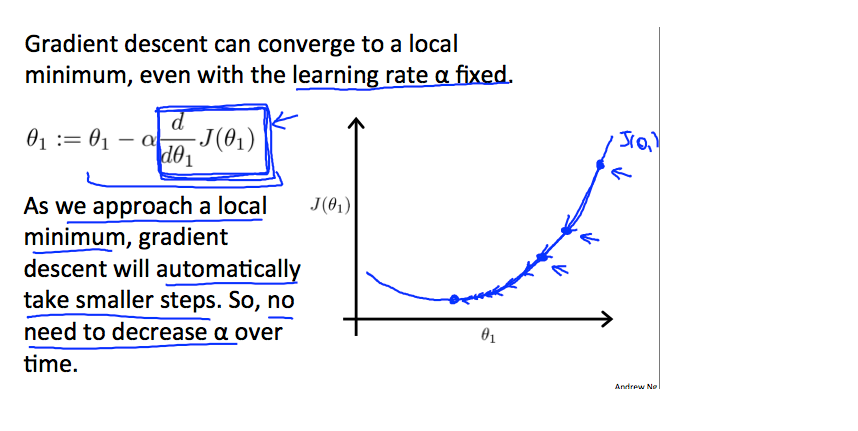

线性回归的梯度下降
当专门应用于线性回归的情况时，可以推导出一种新形式的梯度下降方程。 我们可以替换我们的实际代价函数和我们的实际假设函数，并将方程修改为：
repeat until convergence: {


}

所以，这只是原始代价函数 J 的梯度下降。 这种方法在每一步都查看整个训练集中的每个示例，称为批量梯度下降。 请注意，虽然梯度下降一般容易受到局部最小值的影响，但我们在这里提出的线性回归优化问题只有一个全局最优值，没有其他局部最优值； 因此梯度下降总是收敛（假设学习率 α 不是太大）到全局最小值。 事实上，J 是一个凸二次函数。 这是梯度下降的示例，因为它运行以最小化二次函数。