大间隔分类器
优化目标
支持向量机 (SVM) 是另一种监督机器学习算法。 它有时更干净、更强大。
回想一下,在逻辑回归中,我们使用以下规则: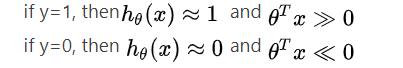
回想一下(非正则化)逻辑回归的成本函数: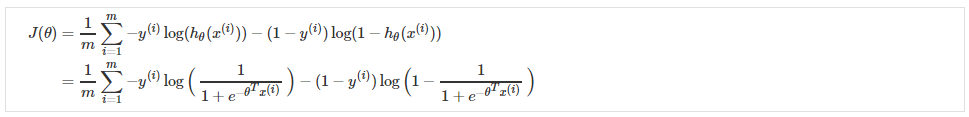
为了制作支持向量机,我们将修改成本函数的第一项因此,当
(从现在开始,我们将其称为 z)大于 1 时,它输出 0。此外,对于 z 小于 1 的值,我们将使用直线下降线而不是 sigmoid 曲线。

同样,我们修改成本函数的第二项所以当 z 小于 -1 时,它输出 0。我们还修改它,以便对于大于 -1 的 z 值,我们使用直线增加线而不是 sigmoid 曲线。


回忆一下(正则化)逻辑回归中的完整成本函数: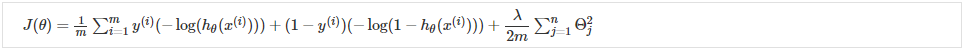
请注意,负号已分配到上述等式中的总和中。我们可以通过代入 和
将其转化为支持向量机的成本函数:
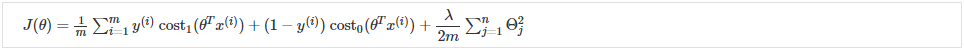
我们可以通过将其乘以 m 来优化它(从而去除分母中的 m 因子)。 请注意,这不会影响我们的优化,因为我们只是将成本函数乘以一个正常数(例如,最小化得到 5;
乘以 10 使其在最小化时仍然得到 5)。
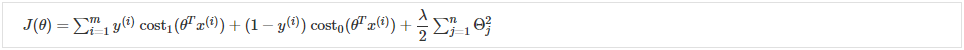
此外,约定要求我们使用因子 C 而不是 λ 进行正则化,如下所示: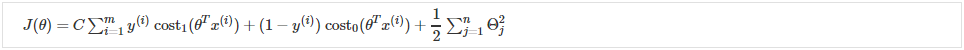
这等效于将方程乘以 ,因此在优化时会产生相同的值。 现在,当我们希望更多地正则化(即减少过拟合)时,我们减小 C,而当我们希望更少地正则化(即减少欠拟合)时,我们增加 C。
最后,请注意支持向量机的假设不被解释为 y 为 1 或 0 的概率(就像逻辑回归假设一样)。 相反,它输出 1 或 0。(用技术术语来说,它是一个判别函数。)
大间隔理解
考虑支持向量机的一种有用方法是将它们视为大边距分类器。
如果 y=1,我们想要 ΘTx≥1(不仅仅是 ≥0)
如果 y=0,我们想要 ΘTx≤−1(不仅仅是 <0)
现在,当我们将常数 C 设置为一个非常大的值(例如 100,000)时,我们的优化函数将约束 Θ,使得方程 A(每个示例的成本总和)等于 0。我们对 Θ 施加以下约束:
如果y=1,则ΘTx≥1,如果y=0,则ΘTx≤-1。
如果 C 非常大,我们必须选择 Θ 参数使得:
∑mi=1y(i)cost1(ΘTx)+(1−y(i))cost0(ΘTx)=0
这将我们的成本函数减少为:
J(θ)=C⋅0+12∑j=1nΘ2j=12∑j=1nΘ2j
回想一下逻辑回归中的决策边界(分隔正例和负例的线)。 在 SVM 中,决策边界具有一个特殊的特性,即它尽可能远离正例和反例。
决策边界到最近示例的距离称为边距。 由于 SVM 最大化了这个裕度,所以它通常被称为大裕度分类器。
SVM 将负例和正例分开很大。
只有当 C 非常大时才能实现如此大的裕度。
当一条直线可以将正例和负例分开时,数据是线性可分的。
如果我们有不想影响决策边界的异常样本,那么我们可以减少 C。
增加和减少C类似于分别减少和增加λ,可以简化我们的决策边界。

