代价函数<br />我们不能使用与线性回归相同的成本函数，因为逻辑函数会导致输出呈波浪状，从而导致许多局部最优。 换句话说，它不会是一个凸函数。相反，我们的逻辑回归成本函数看起来像。<br /><br />当y=1时，和<br />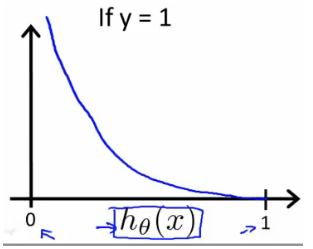<br />当y=0时，和<br />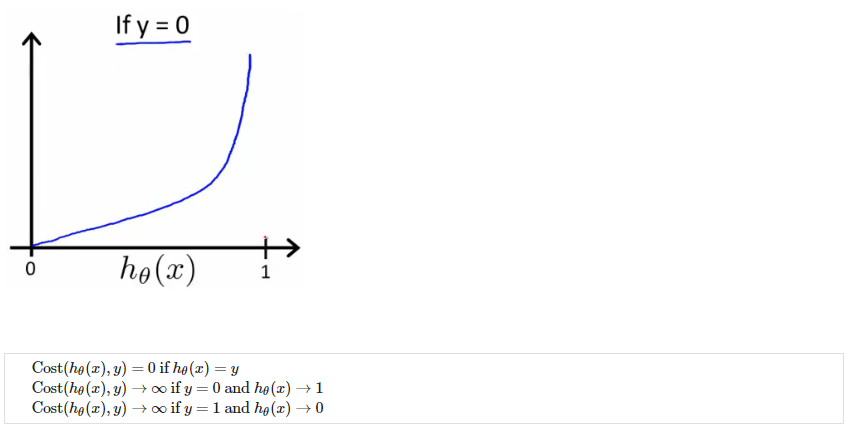<br />如果我们的正确答案 'y' 是 0，那么如果我们的假设函数也输出 0，那么成本函数将是 0。如果我们的假设接近 1，那么成本函数将接近无穷大。<br />如果我们的正确答案 'y' 是 1，那么如果我们的假设函数输出 1，那么成本函数将为 0。如果我们的假设接近 0，那么成本函数将接近无穷大。<br />请注意，以这种方式编写成本函数可以保证 J(θ) 对于逻辑回归是凸的。
简化的代价函数和梯度下降
我们可以将代价函数的两种条件情况压缩为一种情况：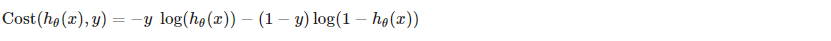
请注意，当 y 等于 1 时，第二项
将为零并且不会影响结果。 如果 y 等于 0，则第一项
将为零且不会影响结果。
我们可以完整地写出我们的整个代价函数如下：
向量化的实现是：
请记住，梯度下降的一般形式是：
我们可以用微积分计算导数部分，得到：
请注意，此算法与我们在线性回归中使用的算法相同。 我们仍然必须同时更新 theta 中的所有值。
向量化的实现是：
已知：
，其中
，计算
。
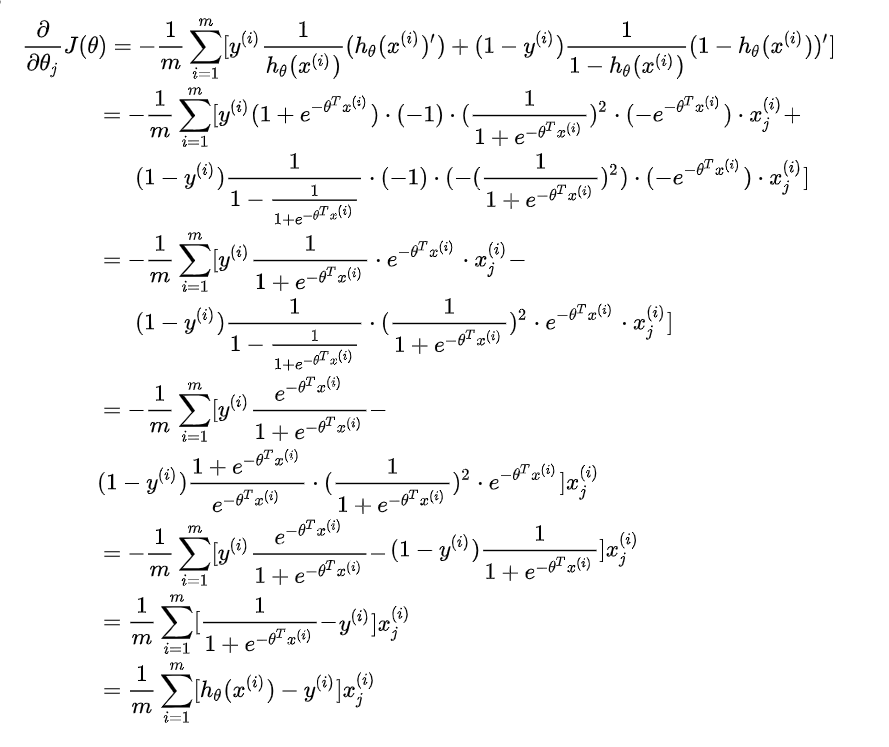
和
为列向量
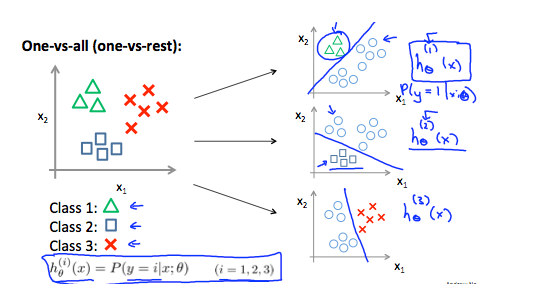
多类分类：一对多
现在，当我们有两个以上的类别时，我们将处理数据的分类。 我们将扩展我们的定义，而不是 y = {0,1}，以便 y = {0,1…n}。由于 y = {0,1…n}，我们将问题分为 n+1（+1，因为索引从 0 开始）二元分类问题； 在每一个中，我们预测 ‘y’ 是我们的一个类的成员的概率。
我们基本上是选择一个类，然后将所有其他类归为一个单一的第二个类。 我们反复这样做，对每个案例应用二元逻辑回归，然后使用返回最高值的假设作为我们的预测。
下图显示了如何对 3 个类别进行分类：
若有收获，就点个赞吧
0 人点赞
