Part 7 解决过拟合问题

过拟合的问题
考虑从x ∈ R预测y的问题。下面最左边的图显示了拟合a的结果到数据集。我们发现数据并不是真的在直线上，所以拟合不是很好。

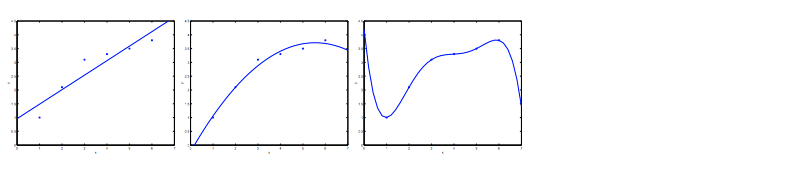
相反，如果我们添加了一个额外的特征 并且适合 ，那么我们会获得更好的数据拟合（见中间图）。 天真地，似乎我们添加的功能越多越好。 但是，添加太多特征也存在危险：最右边的数字是拟合阶多项式的结果。 我们看到，即使拟合曲线完美地通过了数据，我们也不希望这是一个很好的预测指标，例如，不同居住区 (x) 的房价 (y)。 在没有正式定义这些术语的含义的情况下，我们会说左图显示了欠拟合的一个实例——其中数据清楚地显示了模型未捕获的结构——而右图是一个过度拟合的例子。
欠拟合或高偏差是指我们的假设函数 h 的形式与数据趋势的映射不佳。 它通常是由一个功能太简单或使用的功能太少引起的。 在另一个极端，过度拟合或高方差是由拟合可用数据但不能很好地泛化以预测新数据的假设函数引起的。 它通常是由一个复杂的函数引起的，它创建了许多与数据无关的不必要的曲线和角度。
该术语适用于线性回归和逻辑回归。 有两个主要选项可以解决过拟合问题：

代价函数
如果我们的假设函数过度拟合，我们可以通过增加成本来减少函数中某些项的权重。
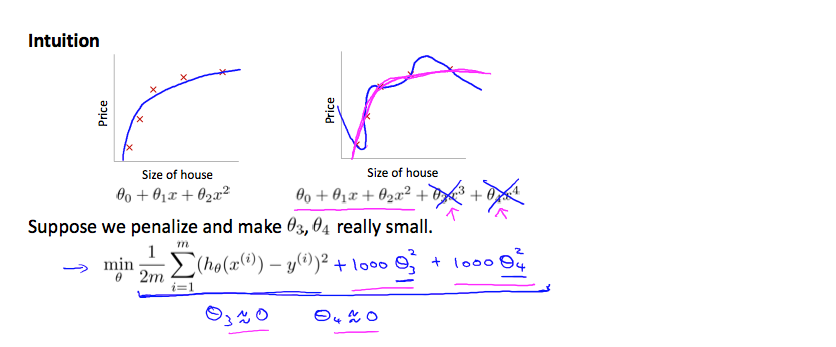
假设我们想让以下函数更二次：

我们想要消除和的影响。在不实际摆脱这些特征或改变我们假设的形式的情况下，我们可以修改我们的成本函数：

我们在末尾添加了两个额外的术语来夸大 和 的成本。 现在，为了使成本函数接近于零，我们必须将 和 的值减小到接近于零。 这反过来将大大降低我们的假设函数中的 和 的值。 结果，我们看到新假设（由粉红色曲线表示）看起来像一个二次函数，但由于额外的小项 和 更适合数据。

我们还可以在一个总和中将所有 theta 参数正则化为：

λ 或 lambda 是正则化参数。 它决定了我们的 theta 参数的成本被夸大了多少。

正则化逻辑回归
我们可以用与正则化线性回归类似的方式来正则化逻辑回归。 因此，我们可以避免过拟合。下图显示了与蓝线表示的非正则化函数相比，粉红色线显示的正则化函数不太可能过度拟合：

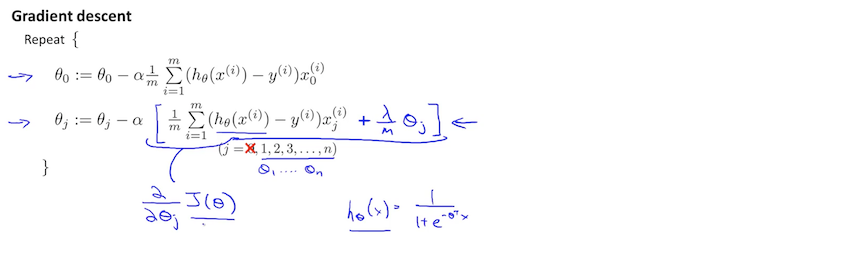
正则化逻辑回归时注意，是单独更新，其他的是如上图所示更新，且theta的范围是从1到n