成本函数<br /> 让我们首先定义一些我们需要使用的变量:<br /> L = 网络中的总层数<br />= 层 l 中的单元数(不计算偏置单元)<br />K = 输出单元/类的数量<br />回想一下,在神经网络中,我们可能有很多输出节点。 我们将表示为导致输出的假设。 我们的神经网络成本函数将是我们用于逻辑回归的成本函数的推广。 回想一下,正则化逻辑回归的成本函数是:<br />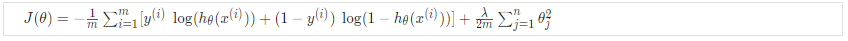<br />对于神经网络,它会稍微复杂一些:<br />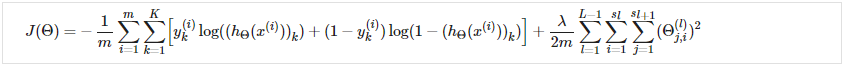<br />我们添加了一些嵌套求和来说明我们的多个输出节点。 在等式的第一部分,在方括号之前,我们有一个额外的嵌套求和,它循环遍历输出节点的数量。<br />在正则化部分,在方括号之后,我们必须考虑多个 theta 矩阵。 我们当前 theta 矩阵中的列数等于我们当前层中的节点数(包括偏置单元)。 我们当前的 theta 矩阵中的行数等于下一层的节点数(不包括偏置单元)。 与之前的逻辑回归一样,我们对每一项进行平方。<br />注意:<br />double sum 简单地将输出层中每个单元格计算的逻辑回归成本相加<br />三重和只是将整个网络中所有单个 Θ 的平方相加。<br />三重总和中的 i 不是指训练示例 i
反向传播算法
“反向传播”是神经网络术语,用于最小化我们的成本函数,就像我们在逻辑回归和线性回归中使用梯度下降所做的一样。 我们的目标是计算:
也就是说,我们希望使用 theta 中的一组最佳参数来最小化我们的成本函数 J。 在本节中,我们将查看用于计算 J(Θ) 偏导数的方程:
为此,我们使用以下算法:
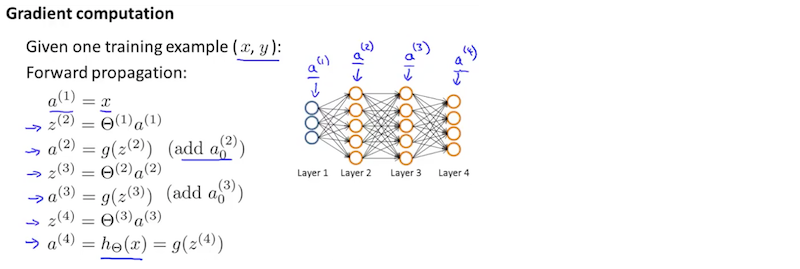

理解反向传播算法
回想一下,神经网络的成本函数是: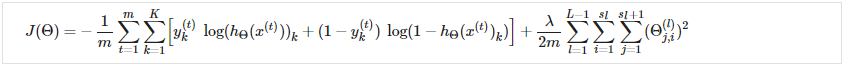
如果我们考虑简单的非多类分类 (k = 1) 并忽略正则化,则成本计算如下:
直观地说,是
(第 l 层中的单元 j)的“错误”。 更正式地说,delta 值实际上是成本函数的导数:

回想一下,我们的导数是与成本函数相切的线的斜率,所以斜率越陡,我们就越不正确。 让我们考虑下面的神经网络,看看我们如何计算一些:
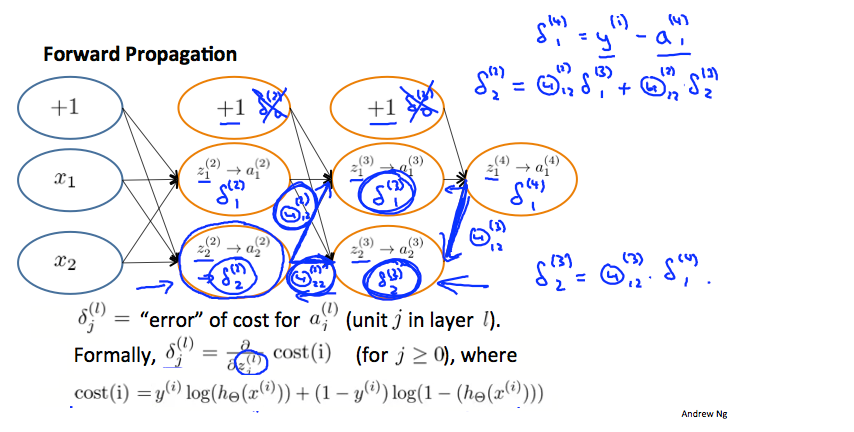
在上图中,为了计算 ,我们将权重
,
乘以在每条边右侧找到的各自
的值。 所以我们得到
. 要计算每一个可能的
,我们可以从图表的右侧开始。 我们可以将我们的边缘视为我们的
. 从右到左,要计算
的值,您只需将每个权重的总和乘以它来自
的权重。 因此,另一个例子是
In the image above, to calculate , we multiply the weights
and
by their respective
values found to the right of each edge. So we get
. To calculate every single possible
, we could start from the right of our diagram. We can think of our edges as our
. Going from right to left, to calculate the value of
, you can just take the over all sum of each weight times the
it is coming from. Hence, another example would be

