Part 4-1 多元线性回归

多元

多个变量的梯度下降

实践中的梯度下降 I - 特征缩放
我们可以通过让每个输入值在大致相同的范围内来加速梯度下降。 这是因为 θ 会在小范围内快速下降而在大范围内缓慢下降，因此当变量非常不均匀时，它会低效地振荡到最优值。防止这种情况的方法是修改我们输入变量的范围，使它们大致相同。
理想情况下：
或者
这些不是确切的要求，我们只是想加快速度。 目标是让所有输入变量大致进入这些范围之一，给出或取一些。有助于解决此问题的两种技术是特征缩放和均值归一化。 特征缩放涉及将输入值除以输入变量的范围（即最大值减去最小值），导致新范围仅为 1。均值归一化涉及从输入变量的值中减去平均值 输入变量导致输入变量的新平均值为零。 要实现这两种技术，请按照以下公式调整输入值：

其中 μi 是特征 (i) 的所有值的平均值，是值的范围（最大值 - 最小值），或者是标准偏差。
例如，如果代表房价范围为 100 到 2000 且平均值为 1000，则

实践中的梯度下降 II - 学习率（ α）
调试梯度下降。 在 x 轴上绘制带有迭代次数的图。 现在在梯度下降的迭代次数上绘制成本函数 J(θ)。 如果 J(θ) 增加，那么您可能需要减少 α。
自动收敛测试。 如果 J(θ) 在一次迭代中减少小于 E，则声明收敛，其中 E 是一些小值，例如 10−3。 但是在实践中很难选择这个阈值。

已经证明，如果学习率 α 足够小，那么 J(θ) 将在每次迭代中减少。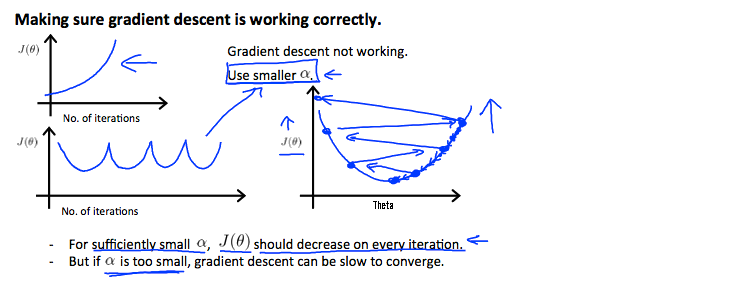

如果 α 太小：收敛慢。
如果 α 太大：可能不会在每次迭代中都减小，因此可能不会收敛。
特征和多项式回归
我们可以通过几种不同的方式改进我们的特征和假设函数的形式。我们可以将多个功能合二为一。 例如，我们可以通过取和 ，将 组合成一个新特征。