Part 9-2 反向传播的应用

实施说明：展开参数
对于神经网络，我们正在处理矩阵集：

为了使用诸如“fminunc()”之类的优化函数，我们需要“展开”所有元素并将它们放入一个长向量中：

如果 Theta1 的尺寸为 10x11，Theta2 为 10x11，Theta3 为 1x11，那么我们可以从“展开”版本中取回原始矩阵，如下所示：

梯度检查
梯度检查将确保我们的反向传播按预期工作。 我们可以用以下方法近似成本函数的导数：

使用多个 theta 矩阵，我们可以近似对 Θj 的导数如下：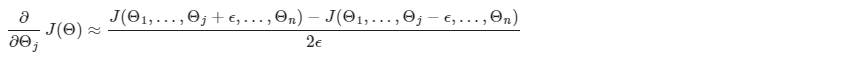

ϵ (epsilon) 的一个小值，例如 ，保证数学计算正确。 如果 ϵ 的值太小，我们最终可能会遇到数值问题。
因此，我们只是在 Θj 矩阵中添加或减去 epsilon。 在matlab中，我们可以这样做：

我们之前看到了如何计算 deltaVector。 因此，一旦我们计算了 gradApprox 向量，我们就可以检查 gradApprox ≈ deltaVector。
一旦您验证了反向传播算法是正确的，您就不需要再次计算 gradApprox。 计算 gradApprox 的代码可能非常慢。

随机初始化
将所有 theta 权重初始化为零不适用于神经网络。 当我们反向传播时，所有节点都会重复更新为相同的值。 相反，我们可以使用以下方法随机初始化 Θ 矩阵的权重：

因此，我们将每个初始化为 [−ϵ,ϵ] 之间的随机值。 使用上面的公式可以保证我们得到所需的界限。 相同的过程适用于所有的 Θ。 下面是一些可用于实验的工作代码。

组合到一起
首先，选择一个网络架构； 选择你的神经网络的布局，包括每层有多少隐藏单元以及你想要总共有多少层。
输入单元数 = 特征维度
输出单元数 = 类数
每层隐藏单元的数量 = 通常越多越好（必须与计算成本平衡，因为它会随着更多隐藏单元的增加而增加）
默认值：1 个隐藏层。 如果您有 1 个以上的隐藏层，那么建议您在每个隐藏层中拥有相同数量的单元。
训练神经网络
随机初始化权重
实施前向传播以获得任何
实现成本函数
实现反向传播以计算偏导数
使用梯度检查来确认您的反向传播有效。 然后禁用梯度检查。
使用梯度下降或内置优化函数来最小化权重为 theta 的成本函数。
当我们执行前向和反向传播时，我们会在每个训练示例上循环：

下图让我们对实现神经网络时发生的事情有一个直观的了解：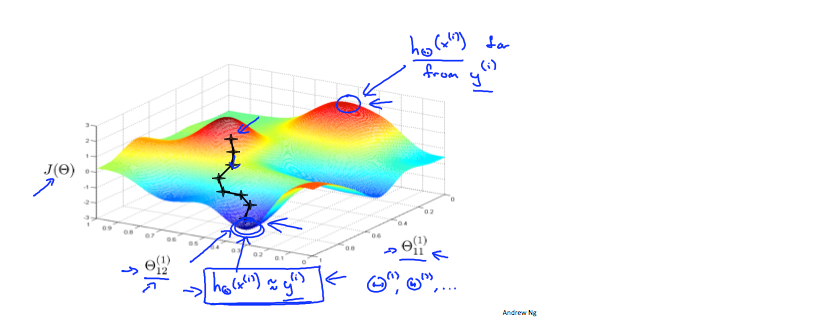

理想情况下，您想要 . 这将最小化我们的成本函数。 但是，请记住，J(Θ) 不是凸的，因此我们最终可以得到局部最小值。