Part 10-2 偏差与方差

诊断偏差与方差
在本节中，我们检查多项式 d 的次数与我们假设的欠拟合或过拟合之间的关系。
我们需要区分偏差或方差是导致错误预测的问题。高偏差是欠拟合，高方差是过拟合。 理想情况下，我们需要在这两者之间找到一个中庸之道。
当我们增加多项式的次数 d 时，训练误差将趋于减少。
同时，交叉验证误差会随着我们将 d 增加到一个点而趋于减少，然后随着 d 的增加而增加，形成一条凸曲线。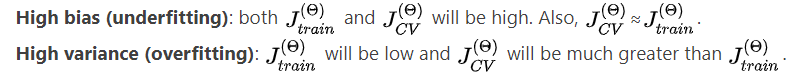

总结如下图：

正则化和偏差/方差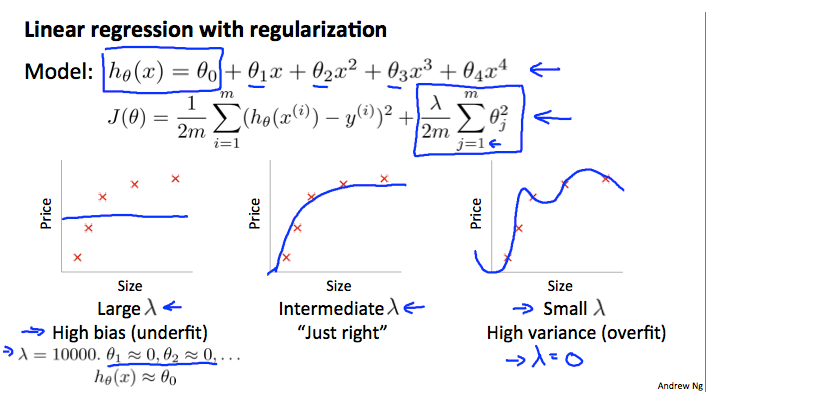

在上图中，我们看到随着增加，我们的拟合变得更加僵硬。 另一方面，随着接近 0，我们倾向于过度拟合数据。 那么我们如何选择我们的参数来让它“恰到好处”呢？ 为了选择模型和正则化项 λ，我们需要：
1、创建一个 lambda 列表（即 λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}）；
2、创建一组具有不同程度或任何其他变体的模型。
3、遍历 s 并且每次遍历所有模型以学习一些 Θ。
4、在没有正则化或 λ = 0 的情况下，使用学习的 Θ在（用 λ 计算）计算交叉验证误差。
5、选择在交叉验证集上产生最低错误的最佳组合。
6、使用最佳组合 Θ 和 λ，将其应用于以查看它是否对问题具有良好的概括性。

学习曲线
在很少数量的数据点（例如 1、2 或 3）上训练算法很容易出现 0 错误，因为我们总能找到一条与这些点数正好相交的二次曲线。 因此：
随着训练集变大，二次函数的误差增加。
误差值将在某个 m 或训练集大小后趋于稳定。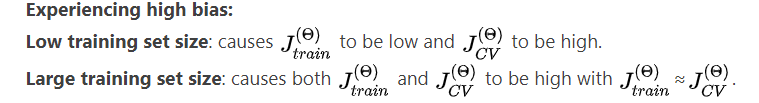

如果学习算法存在高偏差，获得更多的训练数据（就其本身而言）不会有太大帮助。


如果学习算法面临高方差，获取更多训练数据可能会有所帮助。

决定下一步做什么
我们的决策过程可以分解如下：
获取更多训练示例：修复高方差
尝试较小的特征集：修复高方差
添加功能：修复高偏差
添加多项式特征：修复高偏差
减小 λ：修复高偏差
增加 λ：修复高方差。

诊断神经网络
参数较少的神经网络容易欠拟合。 它在计算上也更便宜。
具有更多参数的大型神经网络容易过拟合。 它在计算上也是昂贵的。 在这种情况下，您可以使用正则化（增加 λ）来解决过拟合问题。
使用单个隐藏层是一个很好的初始默认设置。 您可以使用交叉验证集在多个隐藏层上训练神经网络。 然后，您可以选择性能最佳的一种。
模型复杂性影响：
低阶多项式（低模型复杂度）具有高偏差和低方差。 在这种情况下，模型的一致性很差。
高阶多项式（高模型复杂度）非常适合训练数据，而测试数据非常差。 这些对训练数据的偏差很小，但方差很高。
实际上，我们希望在两者之间选择一个模型，它可以很好地概括，但也可以很好地拟合数据。