Part 2-1 模型和函数

模型
为了稍微更正式地描述监督学习问题，我们的目标是，给定一个训练集，学习一个函数 h : X → Y，以便 h(x) 是对应 y 值的“好”预测器。 由于历史原因，这个函数 h 被称为假设。 从图片上看，这个过程是这样的：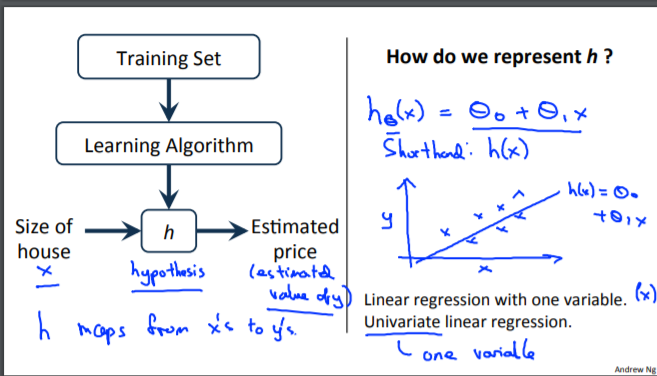

当我们试图预测的目标变量是连续的时，例如在我们的住房示例中，我们将学习问题称为回归问题。 当 y 只能采用少量离散值时（例如，如果给定居住面积，我们想预测住宅是房屋还是公寓），我们称之为分类问题。
通过学习算法(learning algorithm)对已知数据集(training set)进行训练得出函数h，把需要进行预测的数据x代入，得到预测值y
代价函数

我们可以使用代价函数来衡量假设函数的准确性。 这需要假设的所有结果与来自 x 的输入和实际输出 y 的平均差异（实际上是平均值的更高级版本）。

注意J函数的自变量，通过对平方差的求和，算出最小的两个自变量。m表示训练集的个数
一个变量的代价函数
如果我们尝试从视觉角度考虑，我们的训练数据集分散在 x-y 平面上。 我们试图通过这些分散的数据点制作一条直线（定义为）。我们的目标是获得最好的生产线。 可能的最佳线应使散点与线的平均垂直距离平方最小。 理想情况下，这条线应该穿过我们训练数据集的所有点。 在这种情况下， 的值为 0。 以下示例显示了代价函数为 0 的理想情况。

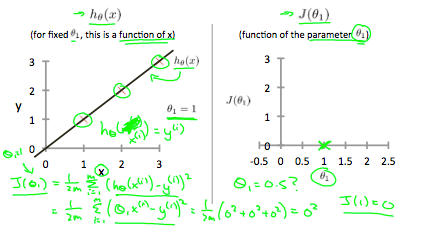
当时，我们得到的斜率为 1，它通过我们模型中的每个数据点。当时，我们看到从拟合到数据点的垂直距离增加了。

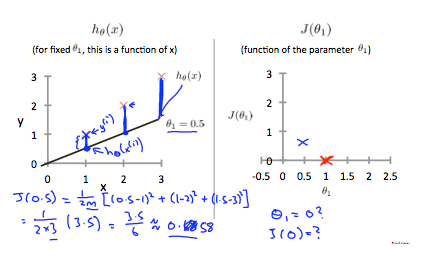
这将我们的代价函数增加到 0.58。 绘制其他几个点会产生下图：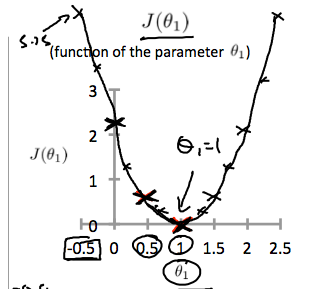

因此我们应该尝试最小化代价函数。如上图所示，当时，取到最小值。
两个变量的代价函数
等高线图是包含许多等高线的图形。 二变量函数的等高线在同一条线的所有点处具有恒定值。 这种图表的一个例子是下面右边的那个。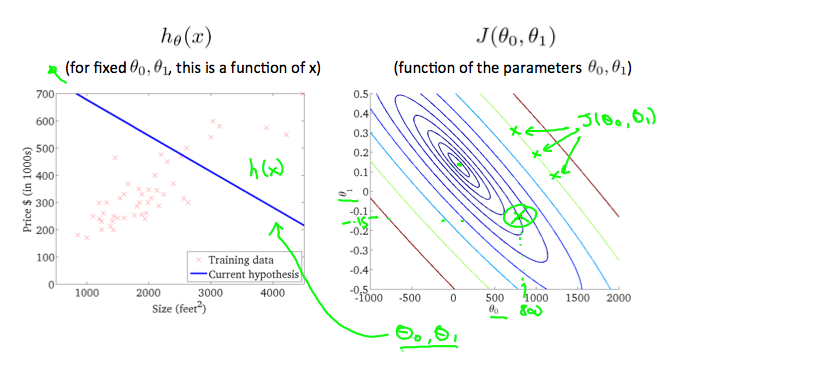

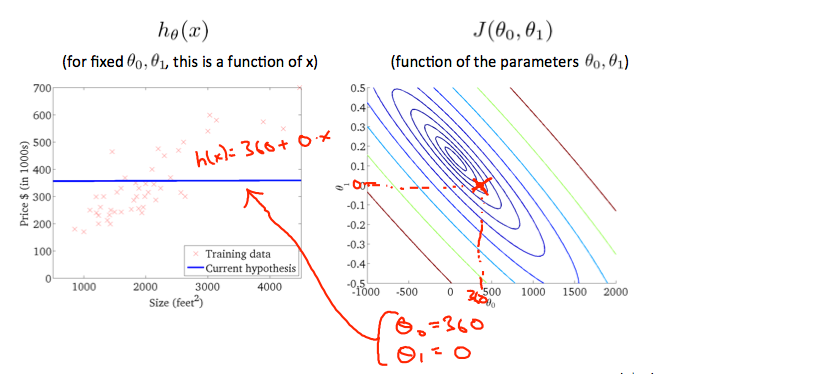
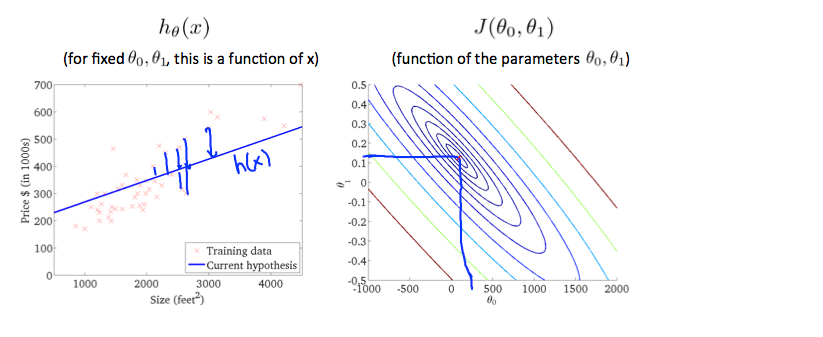
此节给出了等高线图来分析拟合程度，每一条圆弧代表J值相同的所有h(x)，通常最内圈的函数代价最小。