模型展示——1<br />让我们来看看我们将如何使用神经网络来表示假设函数。 在一个非常简单的层面上,神经元基本上是将输入(树突)作为电输入(称为“尖峰”)的计算单元,这些输入被引导到输出(轴突)。 在我们的模型中,我们的树突就像输入特征,输出是我们假设函数的结果。 在这个模型中,我们的输入节点有时被称为“偏置单元”。 它总是等于 1。在神经网络中,我们使用与分类相同的逻辑函数,,但我们有时称其为 sigmoid(逻辑)激活函数。 在这种情况下,我们的“theta”参数有时称为“权重”。<br />在视觉上,一个简单的表示看起来像:<br /><br />我们的输入节点(第 1 层),也称为“输入层”,进入另一个节点(第 2 层),最终输出假设函数,称为“输出层”。<br />我们可以在输入层和输出层之间有中间节点层,称为“隐藏层”。在本例中,我们将这些中间或“隐藏”层节点标记为并且称他们为“激活单元”。<br /><br />如果我们有一个隐藏层,它看起来像:<br /><br />每个“激活”节点的值按如下方式获得:<br /><br />这就是说我们通过使用 3×4 参数矩阵来计算我们的激活节点。 我们将每一行参数应用于我们的输入以获得一个激活节点的值。 我们的假设输出是应用于激活节点值总和的逻辑函数,这些值已乘以另一个包含第二层节点权重的参数矩阵。每层都有自己的权重矩阵, 。<br />这些权重矩阵的维度确定如下:<br />如果网络在第 j 层有单元,在第 j+1 层有单元,则维度为 。<br />+1 来自“偏置节点”和 的添加。 换句话说,输出节点将不包括偏置节点,而输入将包括。 下图总结了我们的模型表示:<br /><br />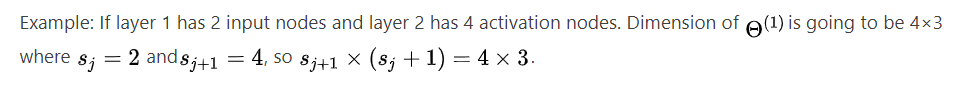<br /> <br />模型展示——2<br />重申一遍,下面是一个神经网络的例子:<br /><br />在本节中,我们将对上述函数进行矢量化实现。 我们将定义一个包含 g 函数内部参数的新变量 在我们之前的示例中,如果我们将所有参数替换为变量 z,我们将得到:<br /><br />换句话说,对于层 j=2 和节点 k,变量 z 将是:<br /><br />设置 ,我们可以将方程改写为:<br /><br /> 我们将矩阵,其维度是(其中是激活节点的数量)乘以高度为 (n+1) 的向量。这给了我们带有高度的向量。现在我们可以获得层 j 的激活节点向量,如下所示:<br /> <br />我们的函数 g 可以按元素应用于我们的向量。<br />然后,我们可以在计算 后向第 j 层添加一个偏置单元(等于 1)。 这将是元素并且等于 1。为了计算我们的最终假设,让我们首先计算另一个 z 向量:<br /><br />我们通过将下一个 theta 矩阵与我们刚刚得到的所有激活节点的值相乘来得到这个最终的 z 向量。 最后一个 theta 矩阵将只有一行乘以一列,因此我们的结果是一个数字。 然后我们得到我们的最终结果:<br />请注意,在最后一步中,在第 j 层和第 j+1 层之间,我们正在做与逻辑回归中完全相同的事情。 在神经网络中添加所有这些中间层使我们能够更优雅地产生有趣且更复杂的非线性假设。

