冒泡排序
来源百度百科:
冒泡排序(Bubble Sort,台湾译为:泡沫排序或气泡排序)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端,故名。
算法描述:
i从0开始,i与i+1比较,如果i>i+1,那么就互换i不断增加,直到i<n-1(n是数组元素的个数,n-1是数组已经最后一个元素) ,一趟下来,可以让数组元素中最大值排在数组的最后面
从最简单开始,首先我们创建一个数组,该数组有5位数字:
int[] arrays = {2, 5, 1, 3, 4};
一、第一趟排序
下面我们根据算法的描述来进行代码验算(第一趟排序):
//使用临时变量,让两个数互换int temp;//第一位和第二位比if (arrays[0] > arrays[1]) {//交换temp = arrays[0];arrays[0] = arrays[1];arrays[1] = temp;}//第二位和第三位比if (arrays[1] > arrays[2]) {temp = arrays[1];arrays[1] = arrays[2];arrays[2] = temp;}//第三位和第四位比if (arrays[2] > arrays[3]) {temp = arrays[2];arrays[2] = arrays[3];arrays[3] = temp;}//第四位和第五位比if (arrays[3] > arrays[4]) {temp = arrays[3];arrays[3] = arrays[4];arrays[4] = temp;}
如果前一位的数比后一位的数要大,那么就交换,直到将数组的所有元素都比较了一遍!
经过我们第一趟比较,我们可以发现:最大的值就在数组的末尾了!
一、第二趟排序
第二趟排序跟第一趟排序一样,也是用前一位与后一位比较,如果前一位比后一位要大,那就交换。值得注意的是:并不需要与最后一位比较了,因为在第一趟排序完了,最后一位已经是最大的数了。同理,我们第二趟排序完了之后,倒数第二位也是第二大的数了。
第二趟排序的代码如下:
//第一位和第二位比if (arrays[0] > arrays[1]) {//交换temp = arrays[0];arrays[0] = arrays[1];arrays[1] = temp;}//第二位和第三位比if (arrays[1] > arrays[2]) {temp = arrays[1];arrays[1] = arrays[2];arrays[2] = temp;}//第三位和第四位比if (arrays[2] > arrays[3]) {temp = arrays[2];arrays[2] = arrays[3];arrays[3] = temp;}//第四位不需要和第五位比了,因为在第一趟排序结束后,第五位是最大的了。
三、代码简化
值得说明的是:上面的结果看起来已经是排序好的了,其实是我在测试时数据还不足够乱,如果数据足够乱的话,是需要4(n-1)趟排序的!
但我们从上面的代码就可以发现:第一趟和第二趟的比较、交换代码都是重复的,并且我们的比较都是写死的(0,1,2,3,4),并不通用!
我们的数组有5位数字
- 第一趟需要比较4次
- 第二趟需要比较3次
我们可以根据上面规律推断出:
- 第三趟需要比较2次
- 第四躺需要比较1次
再从上面的规律可以总结出:5位数的数组需要4躺排序的,每躺排序之后次数减1(因为前一趟已经把前一趟数的最大值确定下来了)!
于是我们可以根据for循环和变量将上面的代码进行简化:
int temp;//外层循环是排序的趟数for (int i = 0; i < arrays.length - 1 ; i++) {//内层循环是当前趟数需要比较的次数for (int j = 0; j < arrays.length - i - 1; j++) {//前一位与后一位与前一位比较,如果前一位比后一位要大,那么交换if (arrays[j] > arrays[j + 1]) {temp = arrays[j];arrays[j] = arrays[j + 1];arrays[j + 1] = temp;}}}
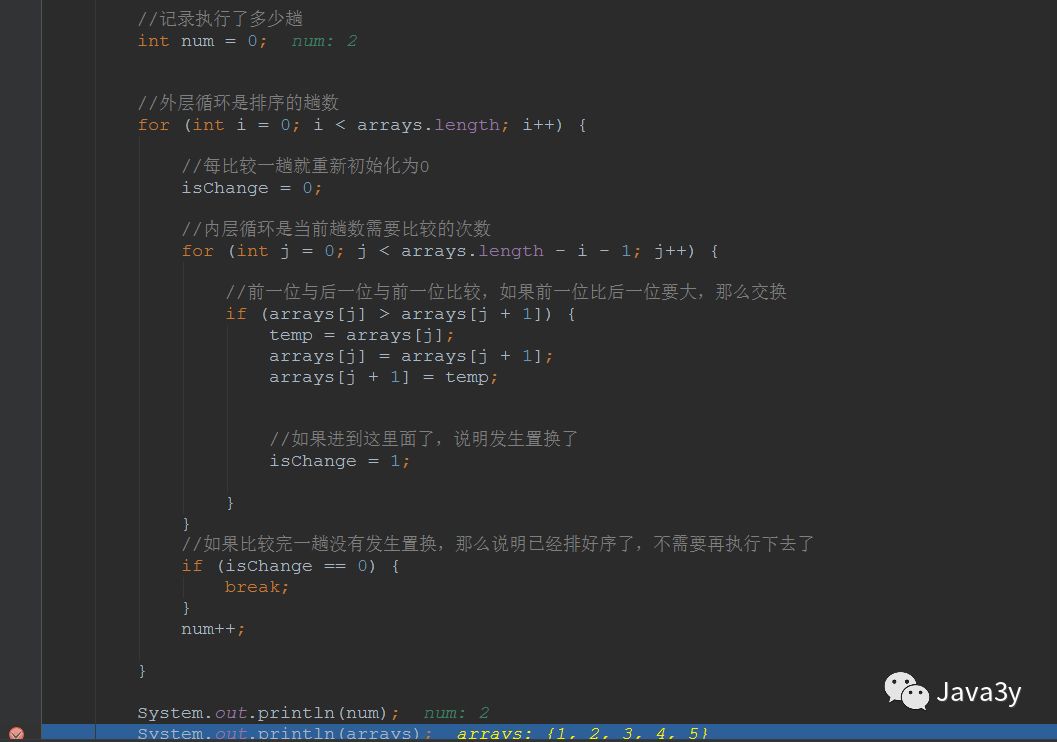
四、冒泡排序优化
从上面的例子我们可以看出来,如果数据足够乱的情况下是需要经过4躺比较才能将数组完整排好序。但是我们在第二躺比较后就已经得到排好序的数组了。
但是,我们的程序在第二趟排序后仍会执行第三趟、第四趟排序。这是没有必要的,因此我们可以对其进行优化一下:
- 如果在某躺排序中没有发生交换位置,那么我们可以认为该数组已经排好序了。
- 这也不难理解,因为我们每趟排序的目的就是将当前趟最大的数置换到对应的位置上,没有发生置换说明就已经排好序了。
代码如下:
//装载临时变量int temp;//记录是否发生了置换, 0 表示没有发生置换、 1 表示发生了置换int isChange;//外层循环是排序的趟数for (int i = 0; i < arrays.length - 1; i++) {//每比较一趟就重新初始化为0isChange = 0;//内层循环是当前趟数需要比较的次数for (int j = 0; j < arrays.length - i - 1; j++) {//前一位与后一位与前一位比较,如果前一位比后一位要大,那么交换if (arrays[j] > arrays[j + 1]) {temp = arrays[j];arrays[j] = arrays[j + 1];arrays[j + 1] = temp;//如果进到这里面了,说明发生置换了isChange = 1;}}//如果比较完一趟没有发生置换,那么说明已经排好序了,不需要再执行下去了if (isChange == 0) {break;}}
五、扩展阅读
C语言实现第一种方式:
void bubble ( int arr[], int n){int i;int temp;for (i = 0; i < n - 1; i++) {if (arr[i] > arr[i + 1]) {temp = arr[i];arr[i] = arr[i + 1];arr[i + 1] = temp;}}}void bubbleSort ( int arr[], int n){int i;for (i = n; i >= 1; i--) {bubble(arr, i);}}
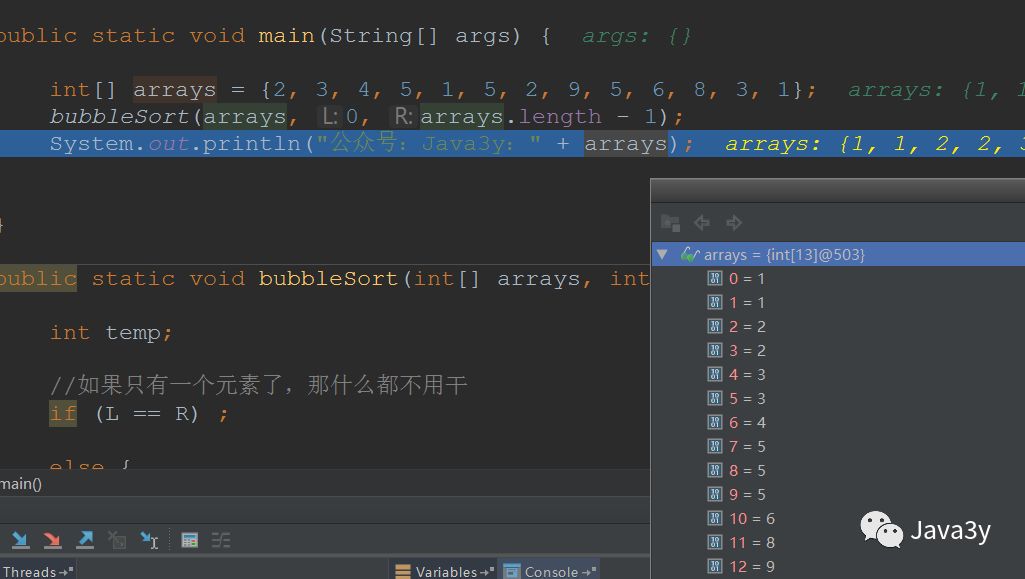
C语言实现第二种方式递归:
void bubble ( int arr[], int L, int R){if (L == R) ;else {int i;for (i = L; i <= R - 1; i++)//i只能到达R-1if (arr[i] > arr[i + 1]) {int temp = arr[i];arr[i] = arr[i + 1];arr[i + 1] = temp;}bubble(arr, L, R - 1);//第一轮已排好R}}
测试代码:
int main (){int arr[] = {2, 3, 4, 511, 66, 777, 444, 555, 9999};bubbleSort(arr, 8);for (int i = 0; i < 9; i++)cout << arr[i] << endl;return 0;}
5.1时间复杂度的理解:

选择排序
从上一篇已经讲解了冒泡排序了,本章主要讲解的是选择排序,希望大家看完能够理解并手写出选择排序的代码,然后就通过面试了!如果我写得有错误的地方也请大家在评论下指出。
选择排序介绍和稳定性说明
来源百度百科:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始(末尾)位置,直到全部待排序的数据元素排完。选择排序是不稳定的排序方法(比如序列[5, 5, 3]第一次就将第一个[5]与[3]交换,导致第一个5挪动到第二个5后面)。
上面提到了选择排序是不稳定的排序方法,那我们的冒泡排序是不是稳定的排序方法呢?稳定的意思指的是什么呢?
判断某排序算法是否稳定,我们可以简单理解成:排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同
- 如果相同,则是稳定的排序方法。
- 如果不相同,则是不稳定的排序方法
如果排序前的数组是[3,3,1],假定我们使用选择排序的话,那第一趟排序后结果就是[1,3,3]。这个数组有两个相同的值,它俩在array[0]和array[1],结果经过排序,array[0]的跑到了array[2]上了。
那么这就导致:2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序不相同,因此,我们就说它是不稳定的
再回到上面的问题,上一篇说讲的冒泡排序是稳定的,主要原因是:俩俩比较的时候,没有对相等的数据进行交换(因为没必要)。因此它不存在2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序不相同。
那么稳定排序的好处是什么?
- 参考知乎回答@独行侠的回答:
如果我们只对一串数字排序,那么稳定与否确实不重要,因为一串数字的属性是单一的,就是数字值的大小。但是排序的元素往往不只有一个属性,例如我们对一群人按年龄排序,但是人除了年龄属性还有身高体重属性,在年龄相同时如果不想破坏原先身高体重的次序,就必须用稳定排序算法.
很清晰的指出,只有当在“二次”排序时不想破坏原先次序,稳定性才有意义
参考资料:
- https://www.zhihu.com/question/46809714/answer/281361290
- http://tieba.baidu.com/p/872860935
http://www.cnblogs.com/codingmylife/archive/2012/10/21/2732980.html
一、第一趟排序
它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始(末尾)位置,直到全部待排序的数据元素排完
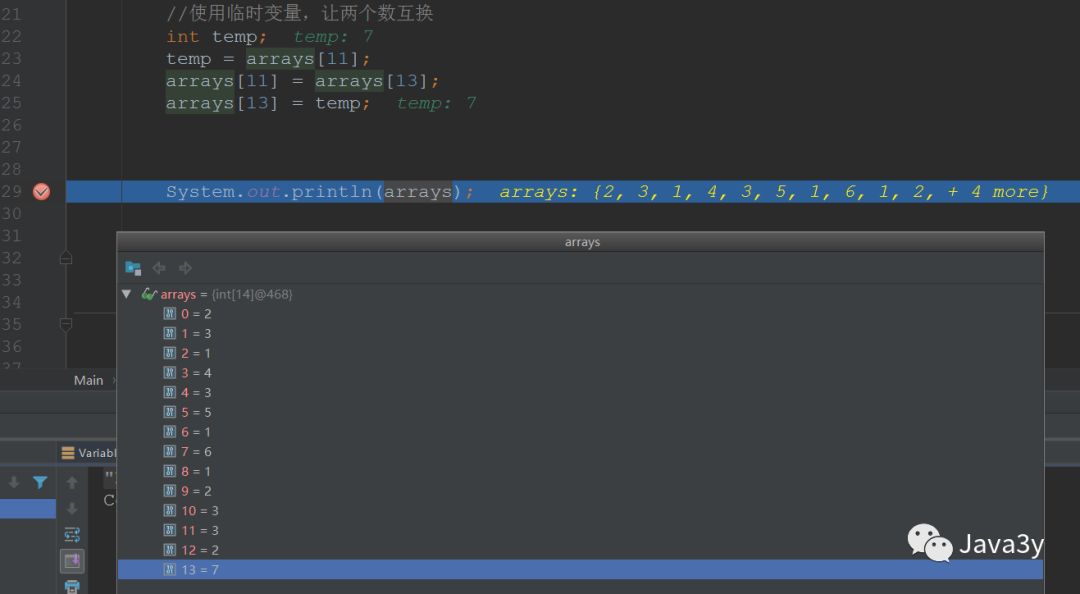
首先,我们创建数组,找到它最大的值(这就很简单了):int[] arrays = {2, 3, 1, 4, 3, 5, 1, 6, 1, 2, 3, 7, 2, 3};//假定max是最大的int max = 0;for (int i = 0; i < arrays.length; i++) {if (arrays[i] > max) {max = arrays[i];}}
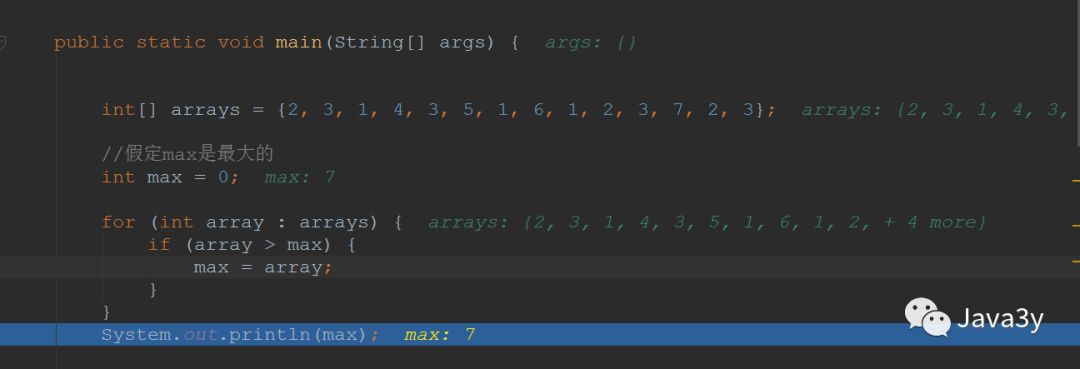
随后这个最大的数和数组末尾的数进行交换://使用临时变量,让两个数互换int temp;temp = arrays[11];arrays[11] = arrays[13];arrays[13] = temp;
二、第二趟排序
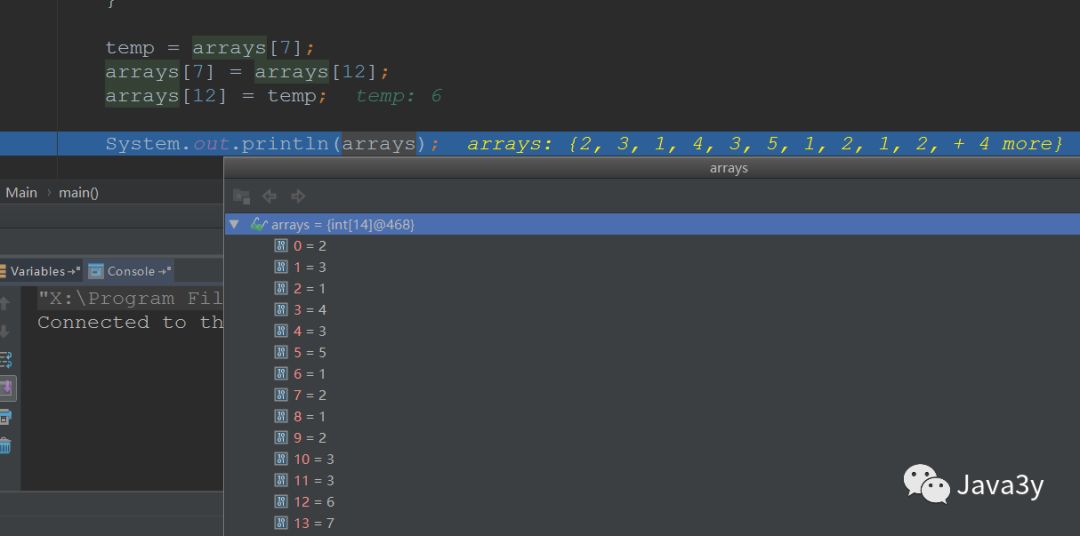
再次从数组获取最大的数(除了已经排好的那个):
int max2 = 0;for (int i = 0; i < (arrays.length - 1); i++) {if (arrays[i] > max2) {max2 = arrays[i];}}System.out.println(max2);
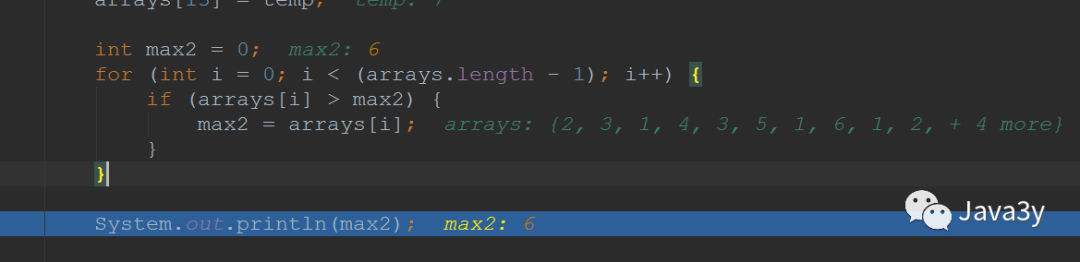
再将获取到的最大值与数组倒数第二位交换:temp = arrays[7];arrays[7] = arrays[12];arrays[12] = temp;
三、代码简化
从前两趟排序其实我们就可以摸出规律了:
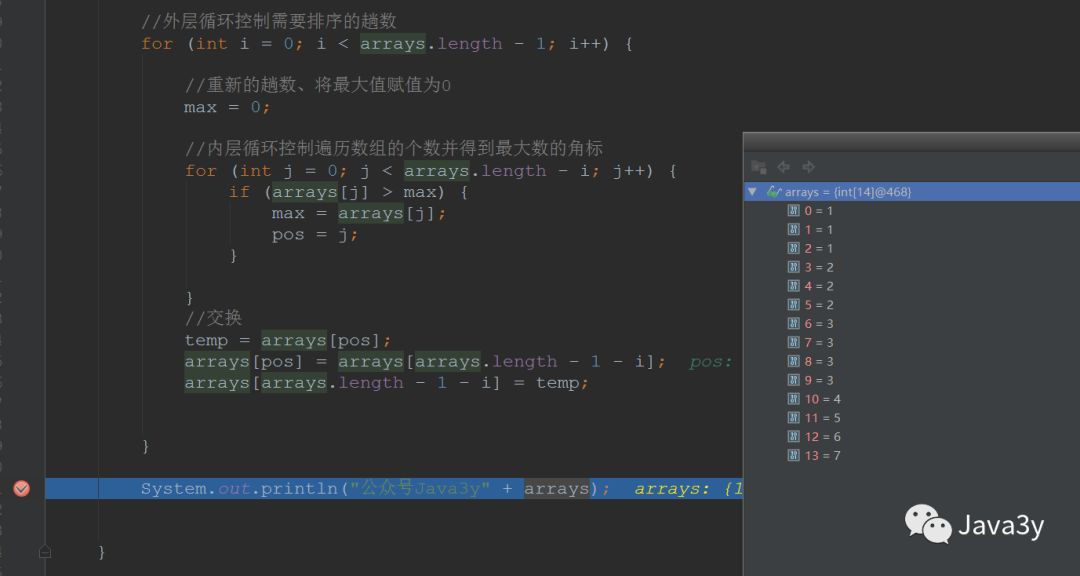
一个数组是需要
n-1趟排序的(因为直到剩下一个元素时,才不需要找最大值)- 每交换1次,再次找最大值时就将范围缩小1
- 查询当前趟数最大值实际上不用知道最大值是多少(上面我查出最大值,还要我手动数它的角标),知道它的数组角标即可,交换也是根据角标来进行交换
第一趟:遍历数组14个数,获取最大值,将最大值放到数组的末尾[13]
第二趟:遍历数组13个数,获取最大值,将最大值放到数组倒数第二位[12]
….
数组有14个数,需要13趟排序。
//记录当前趟数的最大值的角标int pos ;//交换的变量int temp;//外层循环控制需要排序的趟数for (int i = 0; i < arrays.length - 1; i++) {//新的趟数、将角标重新赋值为0pos = 0;//内层循环控制遍历数组的个数并得到最大数的角标for (int j = 0; j < arrays.length - i; j++) {if (arrays[j] > arrays[pos]) {pos = j;}}//交换temp = arrays[pos];arrays[pos] = arrays[arrays.length - 1 - i];arrays[arrays.length - 1 - i] = temp;}System.out.println("公众号Java3y" + arrays);
四、选择排序优化
博主暂未想到比较好的优化方法,如果看到这篇文章的同学知道有更好的优化方法或者代码能够写得更好的地方,欢迎在评论下留言哦!
查到的这篇选择排序优化方法,感觉就把选择排序变了个味,大家也可以去看看:
- 他是同时获取最大值和最小值,然后分别插入数组的首部和尾部(这跟选择排序的原理好像差了点,我也不知道算不算)
- http://www.cnblogs.com/TangMoon/p/7552921.html
五、扩展阅读
C语言实现int findMaxPos ( int arr[], int n){int max = arr[0];int pos = 0;for (int i = 1; i < n; i++) {if (arr[i] > max) {max = arr[i];pos = i;}}return pos;}void selectionSort ( int arr[], int n){while (n > 1){int pos = findMaxPos(arr, n);int temp = arr[pos];arr[pos] = arr[n - 1];arr[n - 1] = temp;n--;//}}int main (){int arr[] = {5, 32, 7, 89, 2, 3, 4, 8, 9};selectionSort(arr, 9);for (int i = 0; i < 9; i++)cout << arr[i] << endl;}
插入排序
从上面已经讲解了冒泡和选择排序了,本章主要讲解的是插入排序,希望大家看完能够理解并手写出插入排序的代码,然后就通过面试了!如果我写得有错误的地方也请大家在评论下指出。
插入排序介绍
来源百度百科:
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。
将一个数据插入到已经排好序的有序数据中
- 将要排序的是一个乱的数组
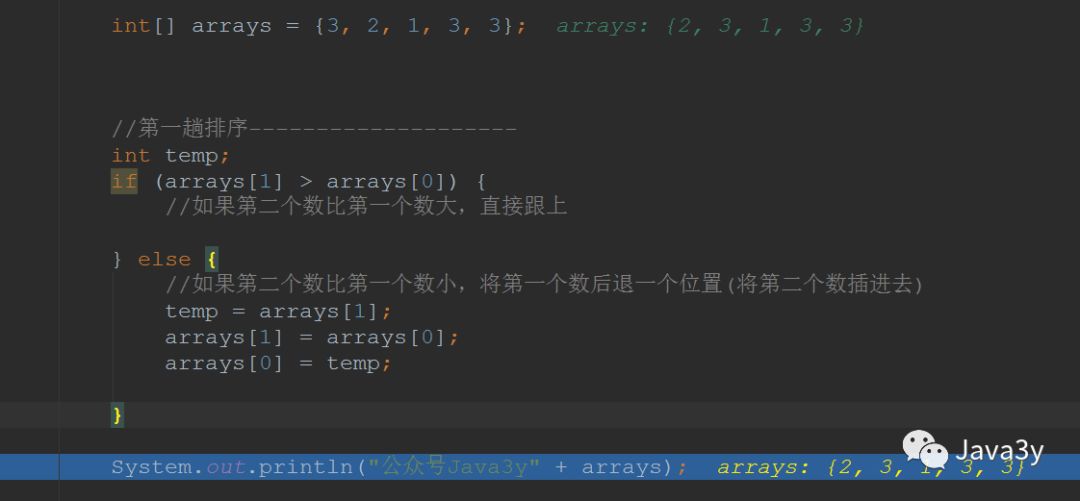
int[] arrays = {3, 2, 1, 3, 3}; 在未知道数组元素的情况下,我们只能把数组的第一个元素作为已经排好序的有序数据,也就是说,把
{3}看成是已经排好序的有序数据一、第一趟排序
用数组的第二个数与第一个数(看成是已有序的数据)比较
如果比第一个数大,那就不管他
如果比第一个数小,将第一个数往后退一步,将第二个数插入第一个数去
int temp;if (arrays[1] > arrays[0]) {//如果第二个数比第一个数大,直接跟上} else {//如果第二个数比第一个数小,将第一个数后退一个位置(将第二个数插进去)temp = arrays[1];arrays[1] = arrays[0];arrays[0] = temp;}System.out.println("公众号Java3y" + arrays);
二、第二趟排序
用数组的第三个数与已是有序的数据
{2,3}(刚才在第一趟排的)比较如果比2大,那就不管它
- 如果比2小,那就将2退一个位置,让第三个数和1比较
- 如果第三个数比1大,那么将第三个数插入到2的位置上
- 如果第三个数比1小,那么将1后退一步,将第三个数插入到1的位置上
//第二趟排序--------------------if (arrays[2] > arrays[1]) {//如果第三个数比第二个数大,直接跟上} else {//如果第三个数比第二个数小,将第二个数往后退一个位置,让第三个数跟第一个数比temp = arrays[2];arrays[2] = arrays[1];//如果第三个数比第一个大,那就插入到第二个数中if (temp > arrays[0]) {arrays[1] = temp;} else {//如果第三个数比第一个小,将第三个数插入到第一个数前面int swapTemp = arrays[0];arrays[0] = temp;arrays[1] = swapTemp;}}System.out.println("公众号Java3y" + arrays);
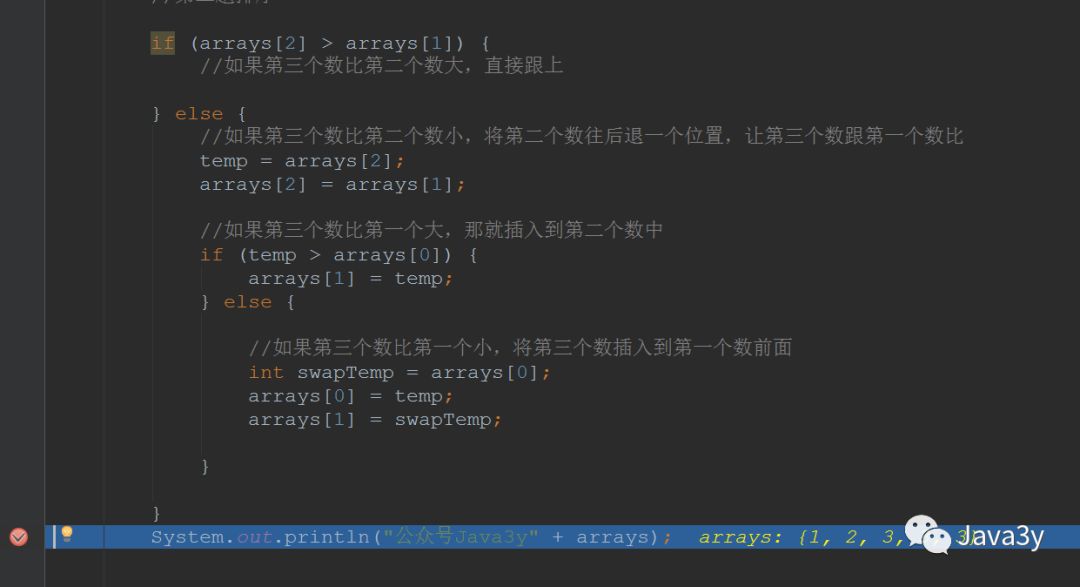
….
三、简化代码
从前两趟排序我们可以摸出的规律:
- 首先将已排序的数据看成一个整体
- 一个数组是需要
n-1趟排序的,总是用后一位跟已排序的数据比较(第一趟:第二位跟已排序的数据比,第二趟:第三位跟已排序的数据比) - 用第三位和
已排序的数据比,实际上就是让第三位数跟两个数比较,只不过这两个数是已经排好序的而已。而正是因为它排好序的,我们可以使用一个循环就可以将我们比较的数据插入进去
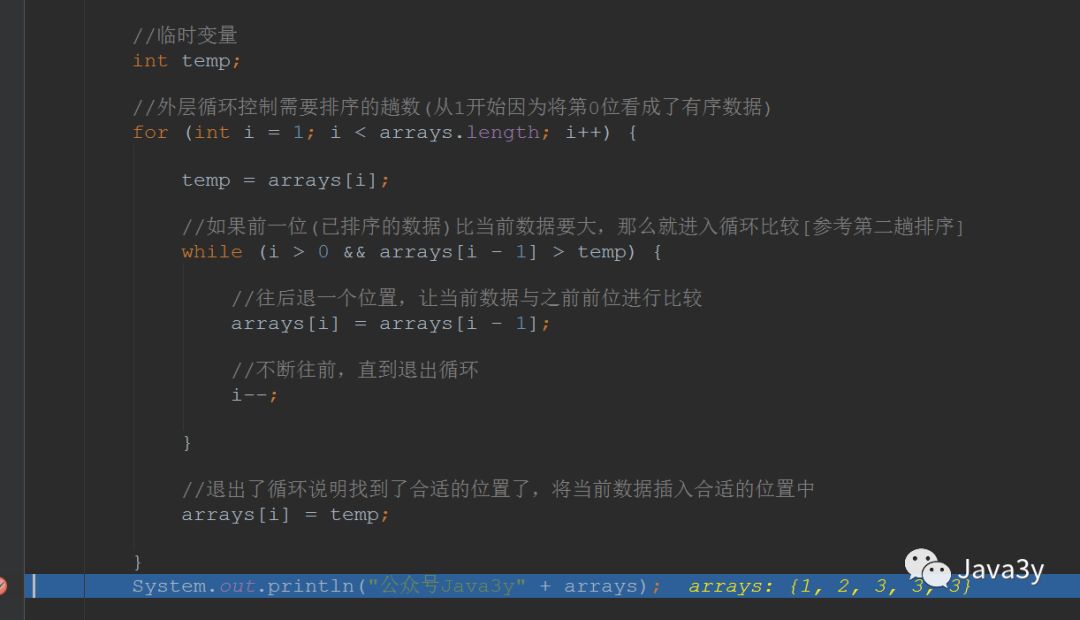
上面的代码还缺少了一个条件:如果当前比较的数据比//临时变量int temp;//外层循环控制需要排序的趟数(从1开始因为将第0位看成了有序数据)for (int i = 1; i < arrays.length; i++) {temp = arrays[i];//如果前一位(已排序的数据)比当前数据要大,那么就进入循环比较[参考第二趟排序]while (arrays[i - 1] > temp) {//往后退一个位置,让当前数据与之前前位进行比较arrays[i] = arrays[i - 1];//不断往前,直到退出循环i--;}//退出了循环说明找到了合适的位置了,将当前数据插入合适的位置中arrays[i] = temp;}
已排序的数据都要小,那么while中的arrays[i - 1]会比0还要小,这会报错的。
我们应该加上一个条件:Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: -1at Main.main(Main.java:61)
i>=1时才可以,如果i=1了下次再进去的时候就退出循环,让当前数据插入到[0]的位置上
所以完整的代码是这样的://临时变量int temp;//外层循环控制需要排序的趟数(从1开始因为将第0位看成了有序数据)for (int i = 1; i < arrays.length; i++) {temp = arrays[i];//如果前一位(已排序的数据)比当前数据要大,那么就进入循环比较[参考第二趟排序]while (i >= 1 && arrays[i - 1] > temp) {//往后退一个位置,让当前数据与之前前位进行比较arrays[i] = arrays[i - 1];//不断往前,直到退出循环i--;}//退出了循环说明找到了合适的位置了,将当前数据插入合适的位置中arrays[i] = temp;}System.out.println("公众号Java3y" + arrays);
四、插入排序优化
二分查找插入排序的原理:是直接插入排序的一个变种,区别是:在有序区中查找新元素插入位置时,为了减少元素比较次数提高效率,采用二分查找算法进行插入位置的确定。
参考资料:http://www.cnblogs.com/heyuquan/p/insert-sort.html
五、扩展阅读
C语言实现第一种方式:
void InsertSortArray ( int arr[], int n){//int arr[]={2,99,3,1,22,88,7,77,54};for (int i = 1; i < n; i++)// 循环从第二个数组元素开始{int temp = arr[i];//temp标记为未排序的第一个元素while (i >= 0 && arr[i - 1] > temp) //将temp与已排序元素从大到小比较,寻找temp应插入的元素{arr[i] = arr[i - 1];i--;}arr[i] = temp;}}
C语言实现第二种方式:
void insert ( int arr[], int n){int key = arr[n];int i = n;while (arr[i - 1] > key) {arr[i] = arr[i - 1];i--;if (i == 0)break;}arr[i] = key;}void insertionSort ( int arr[], int n){int i;for (i = 1; i < n; i++) {insert(arr, i);}}
测试代码:
main(){int arr[] = {99, 2, 3, 1, 22, 88, 7, 77, 54};int i;insertionSort(arr, 9);for (int i = 0; i < 9; i++)cout << arr[i] << endl;return 0;}
参考资料:
- https://www.cnblogs.com/xiaoming0601/p/5862793.html
- http://blog.csdn.net/jianyuerensheng/article/details/51254415
如果文章有错的地方欢迎指正,大家互相交流。习惯在微信看技术文章,想要获取更多的Java资源的同学,可以关注微信公众号:Java3y
快速排序就这么简单
从前面已经讲解了冒泡排序、选择排序、插入排序了,本章主要讲解的是快速排序,希望大家看完能够理解并手写出快速排序的代码,然后就通过面试了!如果我写得有错误的地方也请大家在评论下指出。
快速排序的介绍
来源百度百科:
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序是面试出现的可能性比较高的,也是经常会用到的一种排序,应该重点掌握。
前面一个章节已经讲了递归了,那么现在来看快速排序就非常简单了。
一、第一趟快速排序
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小
百度百科的话并没有说到重点,更简单的理解是这样的:在数组中找一个支点(任意),经过一趟排序后,支点左边的数都要比支点小,支点右边的数都要比支点大!
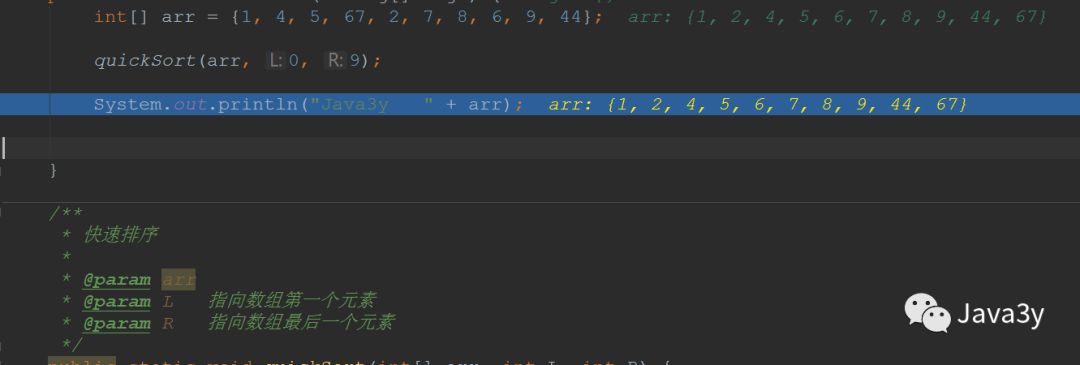
现在我们有一个数组:int arr[]={1,4,5,67,2,7,8,6,9,44};
经过一趟排序之后,如果我选择数组中间的数作为支点:7(任意的),那么第一趟排序后的结果是这样的:{1,4,5,6,2,7,8,67,9,44}
那么就实现了支点左边的数比支点小,支点右边的数比支点大
二、递归分析与代码实现
现在我们的数组是这样的:{1,4,5,6,2,7,8,67,9,44},既然我们比7小的在左边,比7大的在右边,那么我们只要将”左边“的排好顺序,又将”右边“的排好序,那整个数组是不是就有序了?想一想,是不是?
又回顾一下递归:”左边“的排好顺序,”右边“的排好序,跟我们第一趟排序的做法是不是一致的?
只不过是参数不一样:第一趟排序是任选了一个支点,比支点小的在左边,比支点大的在右边。那么,我们想要”左边“的排好顺序,只要在”左边“部分找一个支点,比支点小的在左边,比支点大的在右边。
…………..
在数组中使用递归依照我的惯性,往往定义两个变量:L和R,L指向第一个数组元素,R指向在最后一个数组元素
递归出口也很容易找到:如果数组只有一个元素时,那么就不用排序了
所以,我们可以写出这样的代码:
public static void main(String[] args) {int[] arr = {1, 4, 5, 67, 2, 7, 8, 6, 9, 44};quickSort(arr, 0, 9);System.out.println("Java3y " + arr);}/*** 快速排序** @param arr* @param L 指向数组第一个元素* @param R 指向数组最后一个元素*/public static void quickSort(int[] arr, int L, int R) {int i = L;int j = R;//支点int pivot = arr[(L + R) / 2];//左右两端进行扫描,只要两端还没有交替,就一直扫描while (i <= j) {//寻找直到比支点大的数while (pivot > arr[i])i++;//寻找直到比支点小的数while (pivot < arr[j])j--;//此时已经分别找到了比支点小的数(右边)、比支点大的数(左边),它们进行交换if (i <= j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;i++;j--;}}//上面一个while保证了第一趟排序支点的左边比支点小,支点的右边比支点大了。//“左边”再做排序,直到左边剩下一个数(递归出口)if (L < j)quickSort(arr, L, j);//“右边”再做排序,直到右边剩下一个数(递归出口)if (i < R)quickSort(arr, i, R);}
三、快速排序优化
来源:http://www.cnblogs.com/noKing/archive/2017/11/29/7922397.html
我这里简单概括一下思路,有兴趣的同学可到上面的链接上阅读:
- 随机选取基准值base(支点随机选取)
- 配合着使用插入排序(当问题规模较小时,近乎有序时,插入排序表现的很好)
-
四、扩展阅读
原理都是一样的,在细节上有些变化而已
它是交换完毕后记录支点的角标,然后再劈开两半进行递归调用
C语言代码实现:
void QuickSort ( int*arr,int low, int high);int FindPos ( int*arr,int low, int high);int FindPos ( int*arr,int low, int high){int val = arr[low];while (low < high) {while (low < high && arr[high] >= val)--high;arr[low] = arr[high];while (low < high && arr[low] <= val)++low;arr[high] = arr[low];}arr[low] = val;return low;}void QuickSort ( int arr[], int low, int high){int pos;if (low < high) {pos = FindPos(arr, low, high);QuickSort(arr, low, pos - 1);//劈两半,左边QuickSort(arr, pos + 1, high); //右边}return;}int main (){int arr[ 6]={ 5, 3, -88, 77, 44, -1 } ;int i;QuickSort(arr, 0, 5);for (i = 0; i < 6; i++)printf("%d ", arr[i]);printf("\n");return 0;}
如果文章有错的地方欢迎指正,大家互相交流。习惯在微信看技术文章,想要获取更多的Java资源的同学,可以关注微信公众号:Java3y
归并排序就这么简单
从前面已经讲解了冒泡排序、选择排序、插入排序,快速排序了,本章主要讲解的是归并排序,希望大家看完能够理解并手写出归并排序快速排序的代码,然后就通过面试了!如果我写得有错误的地方也请大家在评论下指出。
归并排序的介绍
来源百度百科:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
过程描述:
归并过程为:比较a[i]和b[j]的大小,若a[i]≤b[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素b[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
原理:
归并操作的工作原理如下: 第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列 第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置 第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置 重复步骤3直到某一指针超出序列尾 将另一序列剩下的所有元素直接复制到合并序列尾
下面我就来做个小小的总结:
- 将两个已排好序的数组合并成一个有序的数组,称之为归并排序
步骤:遍历两个数组,比较它们的值。谁比较小,谁先放入大数组中,直到数组遍历完成
一、演算归并排序过程
现在我有两个已经排好顺序的数组:
int[] arr1 = {2, 7, 8}和int[] arr2 = {1, 4, 9},我还有一个大数组来装载它们int[] arr = new int[6];1.1
那么,我将两个数组的值进行比较,谁的值比较小,谁就放入大数组中!
首先,拿出arr1[0]和arr2[0]进行比较,显然是arr2[0]比较小,因此将arr2[0]放入大数组中,同时arr2指针往后一格
所以,现在目前为止arr = {1}1.2
随后,拿
arr1[0]和arr2[1]进行比较,显然是arr1[0]比较小,将arr1[0]放入大数组中,同时arr1指针往后一格
所以,现在目前为止arr = {1,2}1.3
随后,拿
arr1[1]和arr2[1]进行比较,显然是arr2[1]比较小,将arr2[1]放入大数组中,同时arr2指针往后一格
所以,现在目前为止arr = {1,2,4}
……..
遍历到最后,我们会将两个已排好序的数组变成一个已排好序的数组arr = {1,2,4,7,8,9}二、归并排序前提分析(分治法)
从上面的演算我们就直到,归并排序的前提是需要两个已经排好顺序的数组,那往往不会有两个已经排好顺序的数组给我们的呀(一般是杂乱无章的一个数组),那这个算法是不是很鸡肋的呢??
其实并不是的,首先假设题目给出的数组是这样子的:int[] arr = {2, 7, 8, 1, 4, 9};
当我们要做归并的时候就以arr[3]也就元素为1的那个地方分开。是然后用一个指针L指向arr[0],一个指针M指向arr[3],用一个指针R指向arr[5](数组最后一位)。有了指针的帮助,我们就可以将这个数组切割成是两个有序的数组了(操作的方式就可以和上面一样了)
可是上面说了,一般给出的是杂乱无章的一个数组,现在还是达不到要求。比如给出的是这样一个数组:int[] arrays = {9, 2, 5, 1, 3, 2, 9, 5, 2, 1, 8};
此时,我们就得用到分治的思想了:那么我们也可以这样想将
int[] arr = {2, 7, 8, 1, 4, 9};数组分隔成一份一份的,arr[0]它是一个有序的”数组”,arr[1]它也是一个有序的”数组”,利用指针(L,M,R)又可以像操作两个数组一样进行排序。最终合成{2,7}…….再不断拆分合并,最后又回到了我们的arr = {1,2,4,7,8,9},因此归并排序是可以排序杂乱无章的数组的
这就是我们的分治法—->将一个大问题分成很多个小问题进行解决,最后重新组合起来
三、归并代码实现
实现步骤:
- 拆分
- 合并
……..
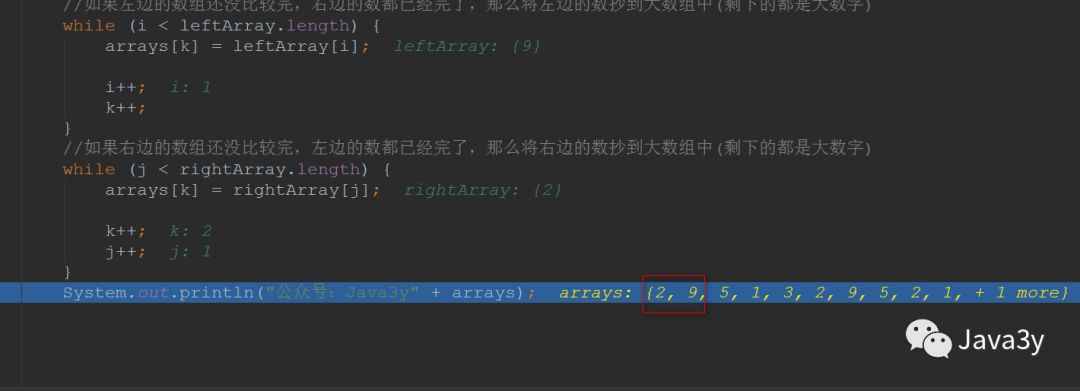
public static void main(String[] args) {int[] arrays = {9, 2, 5, 1, 3, 2, 9, 5, 2, 1, 8};mergeSort(arrays, 0, arrays.length - 1);System.out.println("公众号:Java3y" + arrays);}/*** 归并排序** @param arrays* @param L 指向数组第一个元素* @param R 指向数组最后一个元素*/public static void mergeSort(int[] arrays, int L, int R) {//如果只有一个元素,那就不用排序了if (L == R) {return;} else {//取中间的数,进行拆分int M = (L + R) / 2;//左边的数不断进行拆分mergeSort(arrays, L, M);//右边的数不断进行拆分mergeSort(arrays, M + 1, R);//合并merge(arrays, L, M + 1, R);}}/*** 合并数组** @param arrays* @param L 指向数组第一个元素* @param M 指向数组分隔的元素* @param R 指向数组最后的元素*/public static void merge(int[] arrays, int L, int M, int R) {//左边的数组的大小int[] leftArray = new int[M - L];//右边的数组大小int[] rightArray = new int[R - M + 1];//往这两个数组填充数据for (int i = L; i < M; i++) {leftArray[i - L] = arrays[i];}for (int i = M; i <= R; i++) {rightArray[i - M] = arrays[i];}int i = 0, j = 0;// arrays数组的第一个元素int k = L;//比较这两个数组的值,哪个小,就往数组上放while (i < leftArray.length && j < rightArray.length) {//谁比较小,谁将元素放入大数组中,移动指针,继续比较下一个if (leftArray[i] < rightArray[j]) {arrays[k] = leftArray[i];i++;k++;} else {arrays[k] = rightArray[j];j++;k++;}}//如果左边的数组还没比较完,右边的数都已经完了,那么将左边的数抄到大数组中(剩下的都是大数字)while (i < leftArray.length) {arrays[k] = leftArray[i];i++;k++;}//如果右边的数组还没比较完,左边的数都已经完了,那么将右边的数抄到大数组中(剩下的都是大数字)while (j < rightArray.length) {arrays[k] = rightArray[j];k++;j++;}}
我debug了一下第一次的时候,就可以更容易理解了:
- 将大数组的前两个进行拆分,然后用数组装载起来
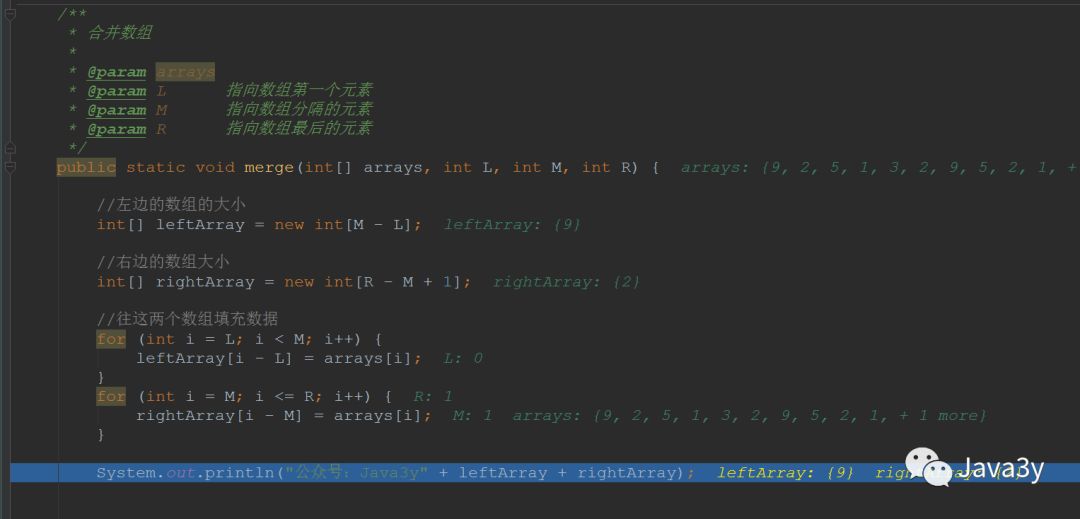
- 比较小数组的元素哪个小,哪个小就先放入大数组中
四、归并排序的优化
来源:http://www.cnblogs.com/noKing/p/7940531.html
我这里整理一下要点,有兴趣的同学可到上面的链接上阅读:
- 当递归到规模足够小时,利用插入排序
- 归并前判断一下是否还有必要归并
- 只在排序前开辟一次空间
二叉树
前言
只有光头才能变强。 文本已收录至我的GitHub仓库,欢迎Star:https://github.com/ZhongFuCheng3y/3y
一、二叉树就是这么简单
本文撇开一些非常苦涩、难以理解的概念来讲讲二叉树,仅入门观看(或复习)….
首先,我们来讲讲什么是树:
- 树是一种非线性的数据结构,相对于线性的数据结构(链表、数组)而言,树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高)
在现实生活中,我们一般的树长这个样子的:
但是在编程的世界中,我们一般把树“倒”过来看,这样容易我们分析:
一般的树是有很多很多个分支的,分支下又有很多很多个分支,如果在程序中研究这个会非常麻烦。因为本来树就是非线性的,而我们计算机的内存是线性存储的,太过复杂的话我们无法设计出来的。
因此,我们先来研究简单又经常用的—-> 二叉树
1.1树的一些概念
我就拿上面的图来进行画来讲解了: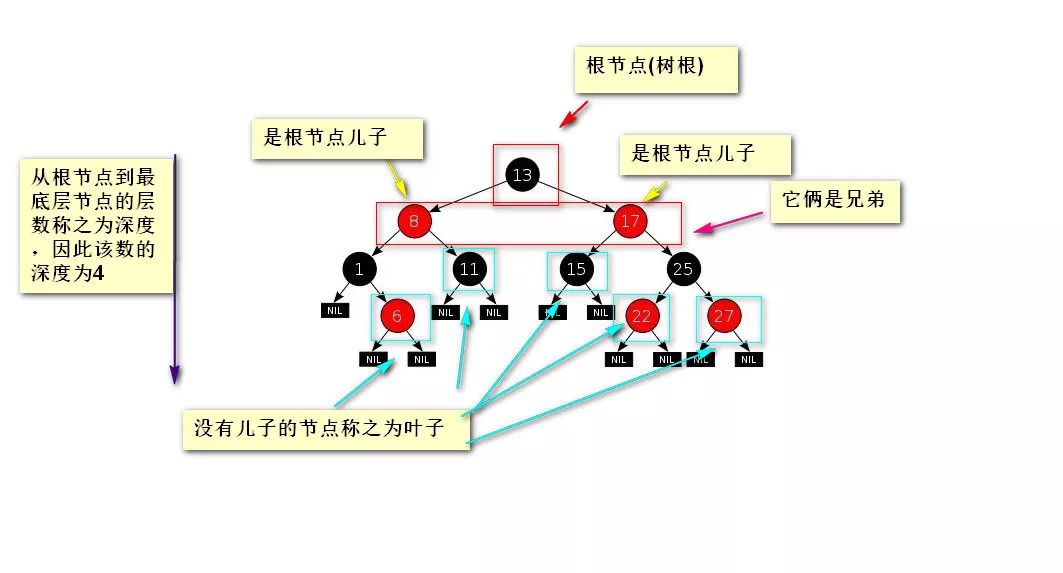
二叉树的意思就是说:每个节点不能多于有两个儿子,上面的图就是一颗二叉树。
- 一棵树至少会有一个节点(根节点)
- 树由节点组成,每个节点的数据结构是这样的:

因此,我们定义树的时候往往是->定义节点->节点连接起来就成了树,而节点的定义就是:一个数据、两个指针(如果有节点就指向节点、没有节点就指向null)
1.2静态创建二叉树
上面说了,树是由若干个节点组成,节点连接起来就成了树,而节点由一个数据、两个指针组成
因此,创建树实际上就是创建节点,然后连接节点
首先,使用Java类定义节点:
public class TreeNode {// 左节点(儿子)private TreeNode lefTreeNode;// 右节点(儿子)private TreeNode rightNode;// 数据private int value;}
下面我们就拿这个二叉树为例来构建吧: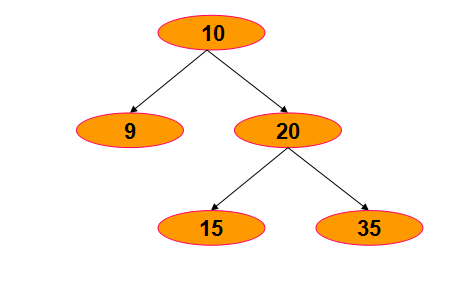
为了方便构建,我就给了它一个带参数的构造方法和set、get方法了:
public TreeNode(int value) {this.value = value;}
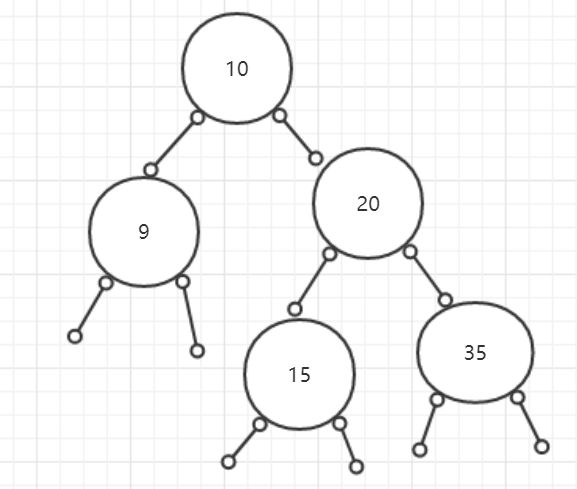
那么我们现在就创建了5个节点:
public static void main(String[] args) {//根节点-->10TreeNode treeNode1 = new TreeNode(10);//左孩子-->9TreeNode treeNode2 = new TreeNode(9);//右孩子-->20TreeNode treeNode3 = new TreeNode(20);//20的左孩子-->15TreeNode treeNode4 = new TreeNode(15);//20的右孩子-->35TreeNode treeNode5 = new TreeNode(35)}
它们目前的状态是这样子的:
于是下面我们去把它连起来:
//根节点的左右孩子treeNode1.setLefTreeNode(treeNode2);treeNode1.setRightNode(treeNode3);//20节点的左右孩子treeNode3.setLefTreeNode(treeNode4);treeNode3.setRightNode(treeNode5);
1.3遍历二叉树
上面说我们的树创建完成了,那怎么证明呢??我们如果可以像数组一样遍历它(看它的数据),那就说明它创建完成了~
值得说明的是:二叉树遍历有三种方式
- 先序遍历
- 先访问根节点,然后访问左节点,最后访问右节点(根->左->右)
- 中序遍历
- 先访问左节点,然后访问根节点,最后访问右节点(左->根->右)
- 后序遍历
- 先访问左节点,然后访问右节点,最后访问根节点(左->右->根)
以上面的二叉树为例:
- 如果是先序遍历:
10->9->20->15->35 - 如果是中序遍历:
9->10->15->20->35- 可能需要解释地方:访问完10节点过后,去找的是20节点,但20下还有子节点,因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就返回20节点,访问20节点。最后访问35节点
- 如果是后序遍历:
9->15->35->20->10- 可能需要解释地方:先访问9节点,随后应该访问的是20节点,但20下还有子节点,因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就去访问35节点,由于35节点也没有儿子了,所以返回20节点,最终返回10节点
一句话总结:先序(根->左->右),中序(左->根->右),后序(左->右->根)。如果访问有孩子的节点,先处理孩子的,随后返回
无论先中后遍历,每个节点的遍历如果访问有孩子的节点,先处理孩子的(逻辑是一样的)
- 因此我们很容易想到递归
- 递归的出口就是:当没有子节点了,就返回
因此,我们可以写出这样的先序遍历代码:
/*** 先序遍历* @param rootTreeNode 根节点*/public static void preTraverseBTree(TreeNode rootTreeNode) {if (rootTreeNode != null) {//访问根节点System.out.println(rootTreeNode.getValue());//访问左节点preTraverseBTree(rootTreeNode.getLefTreeNode());//访问右节点preTraverseBTree(rootTreeNode.getRightNode());}}
结果跟我们刚才说的是一样的: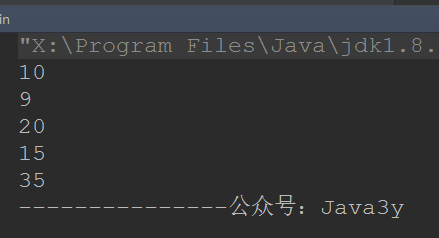
我们再用中序遍历调用一遍吧:
/*** 中序遍历* @param rootTreeNode 根节点*/public static void inTraverseBTree(TreeNode rootTreeNode) {if (rootTreeNode != null) {//访问左节点inTraverseBTree(rootTreeNode.getLefTreeNode());//访问根节点System.out.println(rootTreeNode.getValue());//访问右节点inTraverseBTree(rootTreeNode.getRightNode());}}
结果跟我们刚才说的是一样的: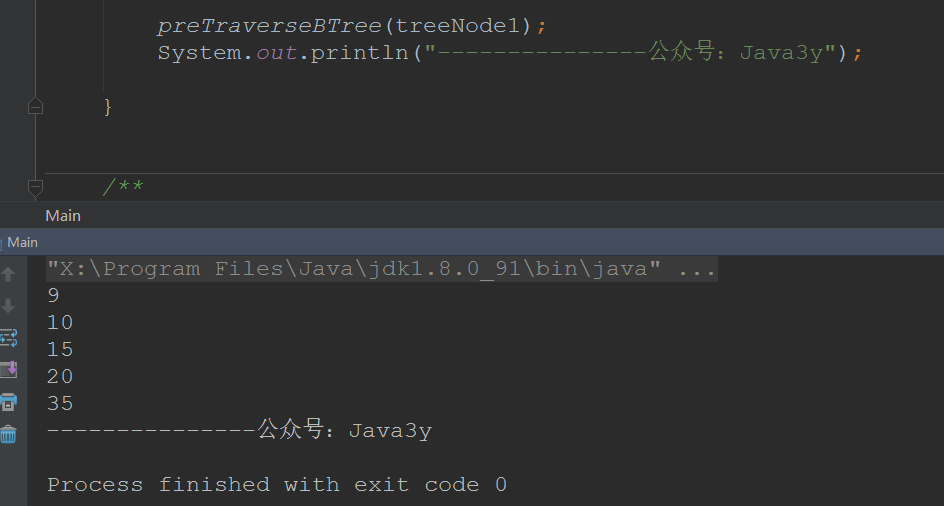
有意思的是:通过先序和中序或者中序和后序我们可以还原出原始的二叉树,但是通过先序和后序是无法还原出原始的二叉树的
也就是说:通过中序和先序或者中序和后序我们就可以确定一颗二叉树了!
二、动态创建二叉树
上面我们是手动创建二叉树的,一般地:都是给出一个数组给你,让你将数组变成一个二叉树,此时就需要我们动态创建二叉树了。
二叉树中还有一种特殊的二叉树:二叉查找树(binary search tree)定义:当前根节点的左边全部比根节点小,当前根节点的右边全部比根节点大。
- 明眼人可以看出,这对我们来找一个数是非常方便快捷的
2.1动态创建二叉树体验
假设我们有一个数组: int[]arrays={3,2,1,4,5};
那么创建二叉树的步骤是这样的:
- 首先将3作为根节点

- 随后2进来了,我们跟3做比较,比3小,那么放在3的左边
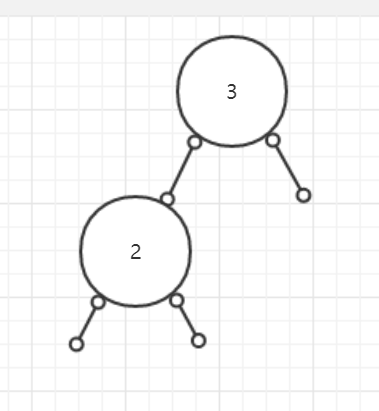
- 随后1进来了,我们跟3做比较,比3小,那么放在3的左边,此时3的左边有2了,因此跟2比,比2小,放在2的左边
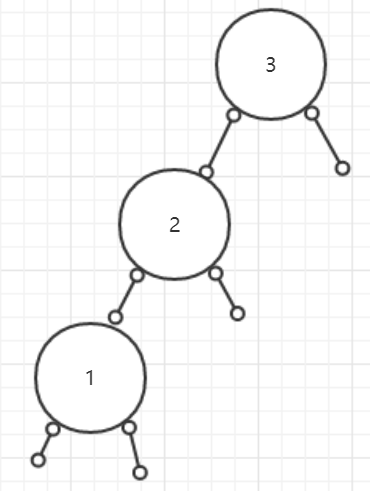
- 随后4进来了,我们跟3做比较,比3大,那么放在3的右边
- 随后5进来了,我们跟3做比较,比3大,那么放在3的右边,此时3的右边有4了,因此跟4比,比4大,放在4的右边
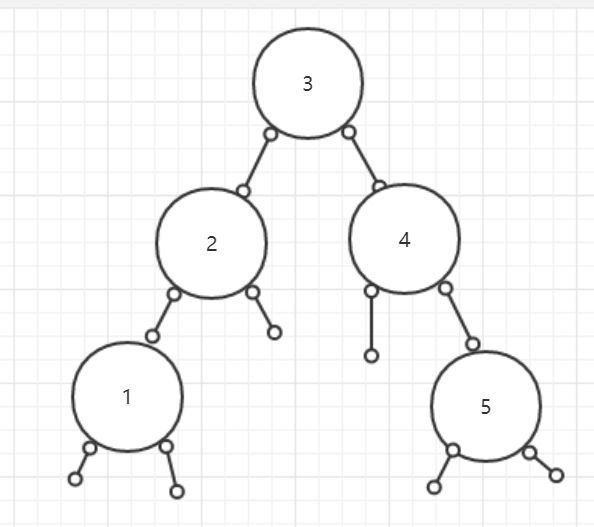
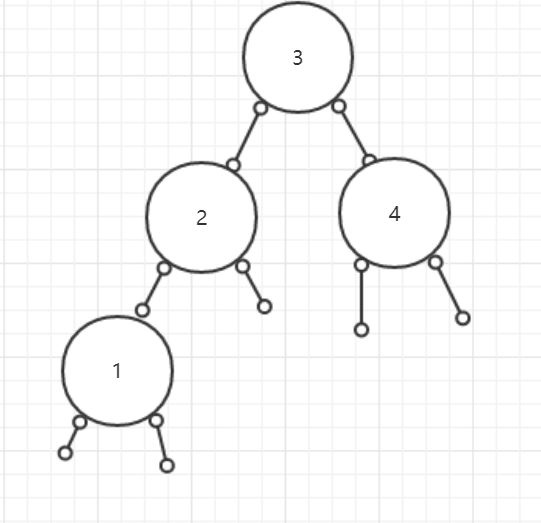
那么我们的二叉查找树就建立成功了,无论任何一颗子树,左边都比根要小,右边比根要大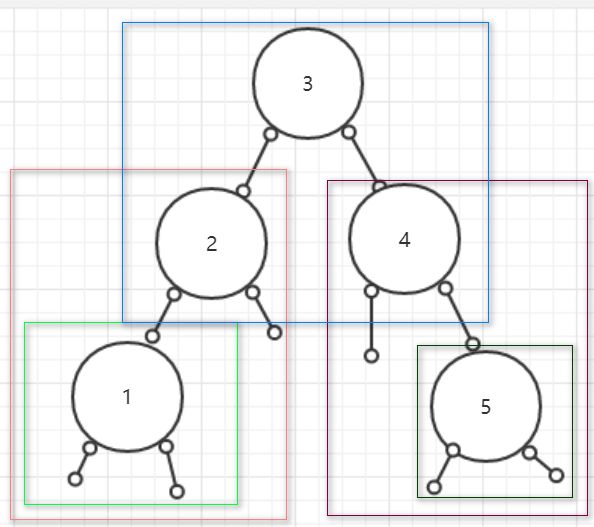
2.2代码实现
我们的代码实现也很简单,如果比当前根节点要小,那么放到当前根节点左边,如果比当前根节点要大,那么放到当前根节点右边。
因为是动态创建的,因此我们得用一个类来表示根节点
public class TreeRoot {private TreeNode treeRoot;public TreeNode getTreeRoot() {return treeRoot;}public void setTreeRoot(TreeNode treeRoot) {this.treeRoot = treeRoot;}}
比较与根谁大,大的往右边,小的往左边:
/*** 动态创建二叉查找树** @param treeRoot 根节点* @param value 节点的值*/public static void createTree(TreeRoot treeRoot, int value) {//如果树根为空(第一次访问),将第一个值作为根节点if (treeRoot.getTreeRoot() == null) {TreeNode treeNode = new TreeNode(value);treeRoot.setTreeRoot(treeNode);} else {//当前树根TreeNode tempRoot = treeRoot.getTreeRoot();while (tempRoot != null) {//当前值大于根值,往右边走if (value > tempRoot.getValue()) {//右边没有树根,那就直接插入if (tempRoot.getRightNode() == null) {tempRoot.setRightNode(new TreeNode(value));return ;} else {//如果右边有树根,到右边的树根去tempRoot = tempRoot.getRightNode();}} else {//左没有树根,那就直接插入if (tempRoot.getLefTreeNode() == null) {tempRoot.setLefTreeNode(new TreeNode(value));return;} else {//如果左有树根,到左边的树根去tempRoot = tempRoot.getLefTreeNode();}}}}}
测试代码:
int[] arrays = {2, 3, 1, 4, 5};//动态创建树TreeRoot root = new TreeRoot();for (int value : arrays) {createTree(root, value);}//中序遍历树inTraverseBTree(root.getTreeRoot());System.out.println("---------------公众号:Java3y");//先序遍历树preTraverseBTree(root.getTreeRoot());System.out.println("---------------公众号:Java3y");三、查询二叉查找树相关
3.1查询树的深度
查询树的深度我们可以这样想:左边的子树和右边的字数比,谁大就返回谁,那么再接上根节点+1就可以了
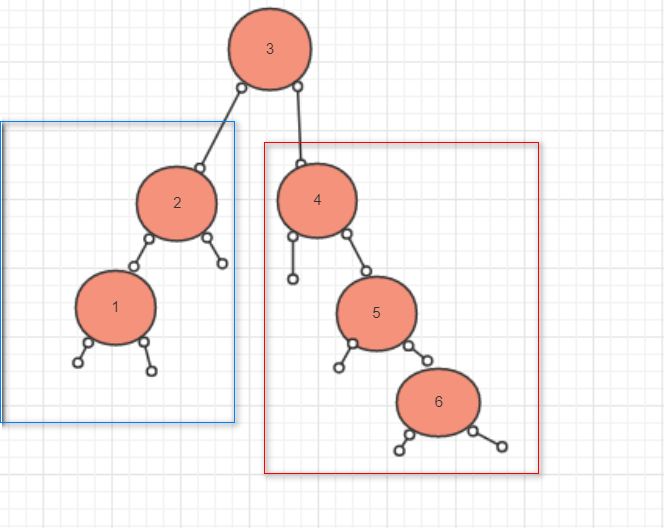
public static int getHeight(TreeNode treeNode) {if (treeNode == null) {return 0;} else {//左边的子树深度int left = getHeight(treeNode.getLefTreeNode());//右边的子树深度int right = getHeight(treeNode.getRightNode());int max = left;if (right > max) {max = right;}return max + 1;}}3.2查询树的最大值
从上面先序遍历二叉查找树的时候,细心的同学可能会发现:中序遍历二叉查找树得到的结果是排好顺序的~
那么,如果我们的二叉树不是二叉查找树,我们要怎么查询他的最大值呢?
可以这样: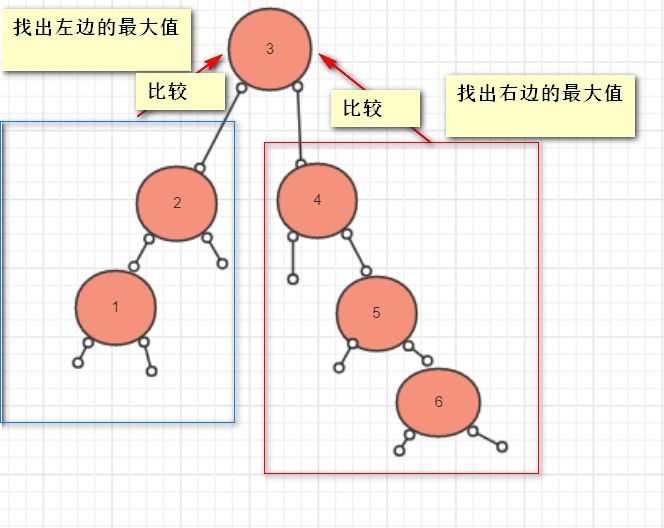
- 左边找最大值->递归
- 右边找最大值->递归
/*** 找出树的最大值** @param rootTreeNode*/public static int getMax(TreeNode rootTreeNode) {if (rootTreeNode == null) {return -1;} else {//找出左边的最大值int left = getMax(rootTreeNode.getLefTreeNode());//找出右边的最大值int right = getMax(rootTreeNode.getRightNode());//与当前根节点比较int currentRootValue = rootTreeNode.getValue();//假设左边的最大int max = left;if (right > max) {max = right;}if (currentRootValue > max) {max = currentRootValue;}return max ;}}四、最后
无论是在遍历树、查找深度、查找最大值都用到了递归,递归在非线性的数据结构中是用得非常多的…
树的应用也非常广泛,此篇简单地说明了树的数据结构,高级的东西我也没弄懂,可能以后用到的时候会继续深入…
递归介绍
本来预算此章节是继续写快速排序的,然而编写快速排序往往是递归来写的,并且递归可能不是那么好理解,于是就有了这篇文章。
在上面提到了递归这么一个词,递归在程序语言中简单的理解是:方法自己调用自己
递归其实和循环是非常像的,循环都可以改写成递归,递归未必能改写成循环,这是一个充分不必要的条件。
- 那么,有了循环,为什么还要用递归呢??在某些情况下(费波纳切数列,汉诺塔),使用递归会比循环简单很多很多
- 话说多了也无益,让我们来感受一下递归吧。
我们初学编程的时候肯定会做过类似的练习:
1+2+3+4+....+100(n)求和- 给出一个数组,求该数组内部的最大值
我们要记住的是,想要用递归必须知道两个条件:
- 递归出口(终止递归的条件)
- 递归表达式(规律)
技巧:在递归中常常是将问题切割成两个部分(1和整体的思想),这能够让我们快速找到递归表达式(规律)
一、求和
如果我们使用for循环来进行求和1+2+3+4+....+100,那是很简单的:
int sum = 0;for (int i = 1; i <= 100; i++) {sum = sum + i;}System.out.println("公众号:Java3y:" + sum);
前面我说了,for循环都可以使用递归来进行改写,而使用递归必须要知道两个条件:1、递归出口,2、递归表达式(规律)
首先,我们来找出它的规律:1+2+3+...+n,这是一个求和的运算,那么我们可以假设X=1+2+3+...+n,可以将1+2+3+...+(n-1)看成是一个整体。而这个整体做的事又和我们的初始目的(求和)相同。以我们的高中数学知识我们又可以将上面的式子看成X=sum(n-1)+n
好了,我们找到我们的递归表达式(规律),它就是sum(n-1)+n,那递归出口呢,这个题目的递归出口就有很多了,我列举一下:
- 如果
n=1时,那么就返回1 - 如果
n=2时,那么就返回3(1+2) - 如果
n=3时,那么就返回6(1+2+3)
当然了,我肯定是使用一个最简单的递归出口了:if(n=1) return 1
递归表达式和递归出口我们都找到了,下面就代码演示:
递归出口为1:
public static void main(String[] args) {System.out.println("公众号:Java3y:" + sum(100));}/**** @param n 要加到的数字,比如题目的100* @return*/public static int sum(int n) {if (n == 1) {return 1;} else {return sum(n - 1) + n;}}
递归出口为4:
public static void main(String[] args) {System.out.println("公众号:Java3y:" + sum(100));}/**** @param n 要加到的数字,比如题目的100* @return*/public static int sum(int n) {//如果递归出口为4,(1+2+3+4)if (n == 4) {return 10;} else {return sum(n - 1) + n;}}
二、数组内部的最大值
如果使用的是循环,那么我们通常这样实现:
int[] arrays = {2, 3, 4, 5, 1, 5, 2, 9, 5, 6, 8, 3, 2};//将数组的第一个假设是最大值int max = arrays[0];for (int i = 1; i < arrays.length; i++) {if (arrays[i] > max) {max = arrays[i];}}System.out.println("公众号:Java3y:" + max);
那如果我们用递归的话,那怎么用弄呢?首先还是先要找到递归表达式(规律)和递归出口
- 我们又可以运用1和整体的思想来找到规律
- 将数组第一个数->
2与数组后面的数->{3, 4, 5, 1, 5, 2, 9, 5, 6, 8, 3, 2}进行切割,将数组后面的数看成是一个整体X={3, 4, 5, 1, 5, 2, 9, 5, 6, 8, 3, 2},那么我们就可以看成是第一个数和一个整体进行比较if(2>X) return 2 else(2<X) return X - 而我们要做的就是找出这个整体的最大值与
2进行比较。找出整体的最大值又是和我们的初始目的(找出最大值)是一样的 - 也就可以写成
if( 2>findMax() )return 2 else return findMax()
- 将数组第一个数->
- 递归出口,如果数组只有1个元素时,那么这个数组最大值就是它了。
使用到数组的时候,我们通常为数组设定左边界和右边界,这样比较好地进行切割
- L表示左边界,往往表示的是数组第一个元素,也就会赋值为0(角标为0是数组的第一个元素)
- R表示右边界,往往表示的是数组的长度,也就会赋值为
arrays.length-1(长度-1在角标中才是代表最后一个元素)
那么可以看看我们递归的写法了:
public static void main(String[] args) {int[] arrays = {2, 3, 4, 5, 1, 5, 2, 9, 5, 6, 8, 3, 1};System.out.println("公众号:Java3y:" + findMax(arrays, 0, arrays.length - 1));}/*** 递归,找出数组最大的值* @param arrays 数组* @param L 左边界,第一个数* @param R 右边界,数组的长度* @return*/public static int findMax(int[] arrays, int L, int R) {//如果该数组只有一个数,那么最大的就是该数组第一个值了if (L == R) {return arrays[L];} else {int a = arrays[L];int b = findMax(arrays, L + 1, R);//找出整体的最大值if (a > b) {return a;} else {return b;}}}
三、冒泡排序递归写法
在冒泡排序章节中给出了C语言的递归实现冒泡排序,那么现在我们已经使用递归的基本思路了,我们使用Java来重写一下看看:
冒泡排序:俩俩交换,在第一趟排序中能够将最大值排到最后面,外层循环控制排序趟数,内层循环控制比较次数
以递归的思想来进行改造:
- 当第一趟排序后,我们可以将数组最后一位(R)和数组前面的数(L,R-1)进行切割,数组前面的数(L,R-1)看成是一个整体,这个整体又是和我们的初始目的(找出最大值,与当前趟数的末尾处交换)是一样的
递归出口:当只有一个元素时,即不用比较了:
L==Rpublic static void main(String[] args) {int[] arrays = {2, 3, 4, 5, 1, 5, 2, 9, 5, 6, 8, 3, 1};bubbleSort(arrays, 0, arrays.length - 1);System.out.println("公众号:Java3y:" + arrays);}public static void bubbleSort(int[] arrays, int L, int R) {int temp;//如果只有一个元素了,那什么都不用干if (L == R) ;else {for (int i = L; i < R; i++) {if (arrays[i] > arrays[i + 1]) {temp = arrays[i];arrays[i] = arrays[i + 1];arrays[i + 1] = temp;}}//第一趟排序后已经将最大值放到数组最后面了//接下来是排序"整体"的数据了bubbleSort(arrays, L, R - 1);}}
四、斐波那契数列
接触过C语言的同学很可能就知道什么是费波纳切数列了,因为往往做练习题的时候它就会出现,它也是递归的典型应用。
菲波那切数列长这个样子:{1 1 2 3 5 8 13 21 34 55..... n }
数学好的同学可能很容易就找到规律了:前两项之和等于第三项
例如:1 + 1 = 22 + 3 = 513 + 21 = 34
如果让我们求出第n项是多少,那么我们就可以很简单写出对应的递归表达式了:
Z = (n-2) + (n-1)
递归出口在本题目是需要有两个的,因为它是前两项加起来才得出第三项的值
同样地,那么我们的递归出口可以写成这样:if(n==1) retrun 1 if(n==2) return 2
下面就来看一下完整的代码吧:public static void main(String[] args) {int[] arrays = {1, 1, 2, 3, 5, 8, 13, 21};//bubbleSort(arrays, 0, arrays.length - 1);int fibonacci = fibonacci(10);System.out.println("公众号:Java3y:" + fibonacci);}public static int fibonacci(int n) {if (n == 1) {return 1;} else if (n == 2) {return 1;} else {return (fibonacci(n - 1) + fibonacci(n - 2));}}
五、汉诺塔算法
图片来源百度百科:

玩汉诺塔的规则很简单:有三根柱子,原始装满大小不一的盘子的柱子我们称为A,还有两根空的柱子,我们分别称为B和C(任选)
- 最终的目的就是将A柱子的盘子全部移到C柱子中
- 移动的时候有个规则:一次只能移动一个盘子,小的盘子不能在大的盘子上面(反过来:大的盘子不能在小的盘子上面)
我们下面就来玩一下:
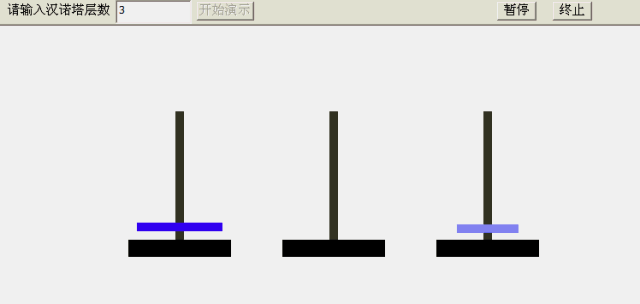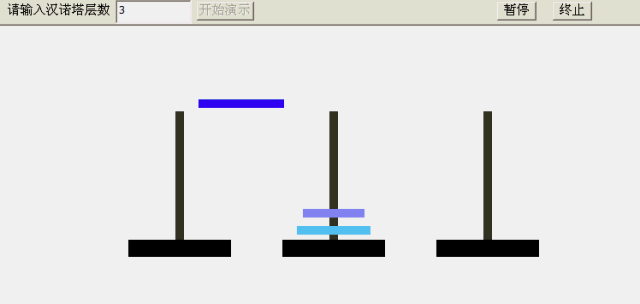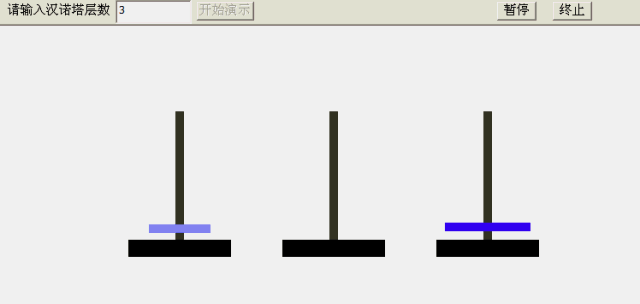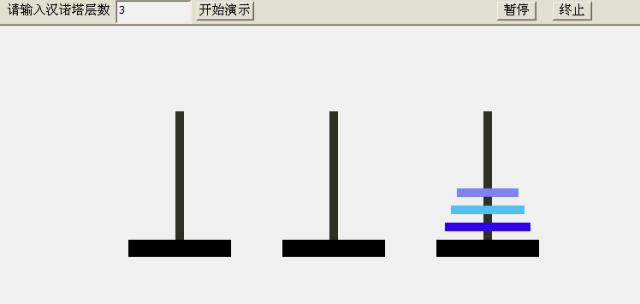
- 只有一个盘子:
- 将A柱子的盘子直接移动到C柱子中
- 完成游戏
- 只有两个盘子:
- 将A柱子上的小盘子移动到B柱子中
- 将A柱子上的大盘子移动到C柱子中
- 最后将在B柱子的小盘子移动到C柱子大盘子中
- 完成游戏
- 只有三个盘子:
- 将A柱子小的盘子移动到C柱子中
- 将A柱子上的中盘子移动到B柱子中
- 将C柱子小盘子移动到B柱子中盘子中
- 将A柱子的大盘子移动到C柱子中
- 将B柱子的小盘子移动到A柱子中
- 将B柱子的中盘子移动到C柱子中
- 最后将A柱子的小盘子移动到C柱子中
- 完成游戏
…………………..
从前三次玩法中我们就可以发现的规律:
- 想要将最大的盘子移动到C柱子,就必须将其余的盘子移到B柱子处(借助B柱子将最大盘子移动到C柱子中[除了最大盘子,将所有盘子移动到B柱子中])[递归表达式]
- 当C柱子有了最大盘子时,所有的盘子在B柱子。现在的目的就是借助A柱子将B柱子的盘子都放到C柱子中(和上面是一样的,已经发生递归了)
- 当只有一个盘子时,就可以直接移动到C柱子了(递归出口)
- A柱子称之为起始柱子,B柱子称之为中转柱子,C柱子称之为目标柱子
- 从上面的描述我们可以发现,起始柱子、中转柱子它们的角色是会变的(A柱子开始是起始柱子,第二轮后就变成了中转柱子了。B柱子开始是目标柱子,第二轮后就变成了起始柱子。总之,起始柱子、中转柱子的角色是不停切换的)
简单来说就分成三步:
- 把 n-1 号盘子移动到中转柱子
- 把最大盘子从起点移到目标柱子
- 把中转柱子的n-1号盘子也移到目标柱子
那么就可以写代码测试一下了(回看上面玩的过程):
public static void main(String[] args) {int[] arrays = {1, 1, 2, 3, 5, 8, 13, 21};//bubbleSort(arrays, 0, arrays.length - 1);//int fibonacci = fibonacci(10);hanoi(3, 'A', 'B', 'C');System.out.println("公众号:Java3y" );}/*** 汉诺塔* @param n n个盘子* @param start 起始柱子* @param transfer 中转柱子* @param target 目标柱子*/public static void hanoi(int n, char start, char transfer, char target) {//只有一个盘子,直接搬到目标柱子if (n == 1) {System.out.println(start + "---->" + target);} else {//起始柱子借助目标柱子将盘子都移动到中转柱子中(除了最大的盘子)hanoi(n - 1, start, target, transfer);System.out.println(start + "---->" + target);//中转柱子借助起始柱子将盘子都移动到目标柱子中hanoi(n - 1, transfer, start, target);}}
我们来测试一下看写得对不对: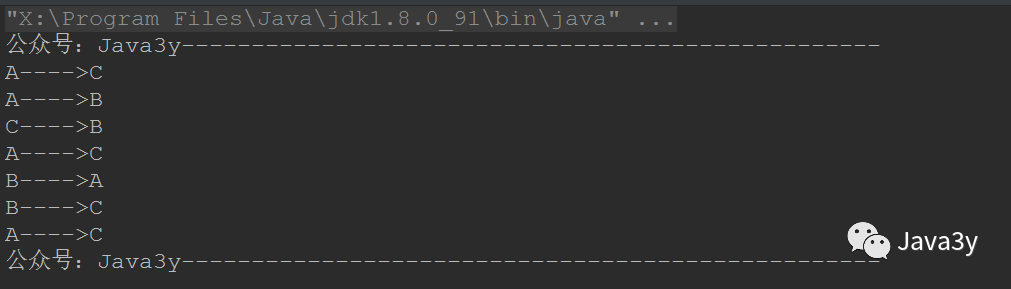
参考资料:
https://www.zhihu.com/question/24385418
六、总结
递归的确是一个比较难理解的东西,好几次都把我绕进去了….
要使用递归首先要知道两件事:递归出口(终止递归的条件)
- 递归表达式(规律)
在递归中常常用”整体“的思想,在汉诺塔例子中也不例外:将最大盘的盘子看成1,上面的盘子看成一个整体。那么我们在演算的时候就很清晰了:将”整体“搬到B柱子,将最大的盘子搬到C柱子,最后将B柱子的盘子搬到C柱子中
因为我们人脑无法演算那么多的步骤,递归是用计算机来干的,只要我们找到了递归表达式和递归出口就要相信计算机能帮我们搞掂。
在编程语言中,递归的本质是方法自己调用自己,只是参数不一样罢了。
最后,我们来看一下如果是5个盘子,要运多少次才能运完: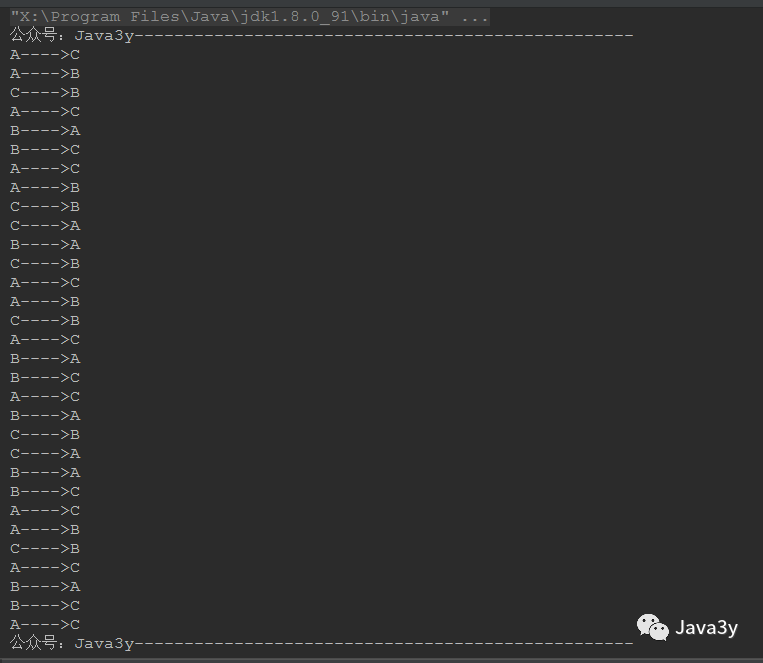
常用查找算法
1.顺序查找
/*** 顺序查找算法* 从数据序列中第一个元素开始,从头到尾依次逐个查找。直到找到所要的数据或搜索完整个数据序列*/public static int searchFun(int a[], int x) {for (int i = 0; i < a.length; i++) {if (a[i] == x) {return i;}}return -1;}
2.折半查找(二分查找)
/*** 折半查找,又称为二分法查找。要求数据序列呈线性结构,也就是经过排序的。* 从数据的1/2处匹配,如果与需要查询的值相等,直接返回,* 如果大于需要查询的关键字,则在从前半部分的1/2处查找,也就是整个数据的1/4处;* 如果小于需要查询的关键字,则从后半部分的1/2处查找,也就是整个数据的3/4出;* 以此类推,直到找到关键字或将查找范围缩小到只剩下一个元素也不等于关键字.*/public static int binarySearch(int a[], int x) {int midNum, lowNum = 0, highNum = a.length - 1;while (lowNum <= highNum) {midNum = (lowNum + highNum) / 2;if (a[midNum] == x) {return midNum;} else if (a[midNum] > x) {highNum = midNum - 1;} else if (a[midNum] < x) {lowNum = midNum + 1;}}return -1;}
3.链表结构中的查找算法
链表结构(下一章总结数据结构,其中有介绍什么是链表结构)也是一种顺序结构,只不过采用的是链式存储的方式。链表结构中的查找算法有点类似于顺序查找的思想
/*** 定义数据结构中的元素*/class DataElement {String key;String other_messages;}/*** 定义链表结构*/class DataLinkedList {DataElement dataElement;DataLinkedList nextNode;//我们这里只做查找算法的示例,省去添加节点,删除节点等其他方法,只做查找/*** 链表结构中的查找算法* 一般来说可以通过关键字查询,从表头依次查找*/DataLinkedList findData(DataLinkedList head, String key) {DataLinkedList temp = head;//保存表头指针while (temp != null) {//节点有效,进行查找DataElement date = temp.dataElement;if (date.key.equals(key)) {//节点的关键字与传入的关键字相同return temp;//返回该节点指针}temp = temp.nextNode;//处理下一节点}return null;//未找到,返回空指针}}
4. 二叉树的查找算法
就是遍历二叉树(下一章中会有介绍什么是树和二叉树),查找对应节点的key是不是匹配关键字
/*** 定义二叉树结构*/static class TreeDate {String data;TreeDate leftData;TreeDate rightData;/*** 二叉树查找算法* 遍历二叉树中的每一个结点,逐个比较数据。* @param treeNode 树结点,首次调用传入树的根结点* @param data 要查找的结点* @return TreeDate查找结果*/TreeDate findData(TreeDate treeNode, String data) {if (treeNode == null) {return null;} else {if (treeNode.data.equals(data)) {return treeNode;}if (findData(treeNode.leftData, data) != null) {//递归查找左结点return findData(treeNode.leftData, data);}if (findData(treeNode.rightData, data) != null) {//递归查找右结点return findData(treeNode.rightData, data);}}return null;}}
5. 图结构中的查找算法
就是遍历图结构(下一章中会有介绍什么是图结构)进行查找
/*** 定义图结构*/static class Graph {static final int SIZE = 5;//图的最大顶点数static final int MAX_VALUE = 65535;//最大值public char[] vertex = new char[SIZE];//保存顶点信息(序号或字母)// int graphType;//图的类型(0.无向图;1.有向图)int vertexNum;//顶点的数量// int edgeNum;//边的数量int[][] edgeWeight = new int[SIZE][SIZE];//保存边的权值int[] isTraversal = new int[SIZE];//遍历标志/*** 深度遍历图* 从第n个顶点开始遍历** @param graph 图* @param n 第n个顶点* @param key 需要查找的顶点*/static void deepTraOne(Graph graph, int n, char key) {graph.isTraversal[n] = 1;//标记该顶点已经处理过if (graph.vertex[n] == key) {//就是要找的结点,如果是进行遍历而不是查找,删除这个判断输出所有结点数据即可System.out.printf("->%c", graph.vertex[n]);//输出结点数据return;}//添加处理结点的操作for (int i = 0; i < graph.vertexNum; i++) {if (graph.edgeWeight[n][i] != MAX_VALUE && graph.isTraversal[n] == 0) {deepTraOne(graph, i, key);//递归遍历}}}/*** 深度优先遍历** @param graph 图* @param key 需要查找的顶点*/static void findVertex(Graph graph, char key) {//清除各顶点遍历标志// for (int i = 0; i < graph.vertexNum; i++) {// graph.isTraversal[i] = 0;// }Arrays.parallelSetAll(graph.isTraversal, index -> 0);//java8的写法,作用同上面的for循环System.out.printf("深度优先遍历结点:");for (int i = 0; i < graph.vertexNum; i++) {if (graph.isTraversal[i] == 0) {//若该点未遍历deepTraOne(graph, i, key);//调用遍历函数}}System.out.printf("\n");}}
查找算法基本就这些,下一章,我们来对上面提到的一些数据结构(链表结构,树结构、二叉树、图结构、有向图、无向图等)进行介绍说明。
30张图带你彻底理解红黑树
写在前面
当在10亿数据中只需要进行10几次比较就能查找到目标时,不禁感叹编程之魅力!人类之伟大呀! —— 学红黑树有感。
终于,在学习了几天的红黑树相关的知识后,我想把我所学所想和所感分享给大家。红黑树是一种比较难的数据结构,要完全搞懂非常耗时耗力,红黑树怎么自平衡?什么时候需要左旋或右旋?插入和删除破坏了树的平衡后怎么处理?等等一连串的问题在学习前困扰着我。如果你在学习过程中也会存在我的疑问,那么本文对你会有帮助,本文帮助你全面、彻底地理解红黑树!
本文将通过图文的方式讲解红黑树的知识点,并且不会涉及到任何代码,相信我,在懂得红黑树实现原理前,看代码会一头雾水的,当原理懂了,代码也就按部就班写而已,没任何难度。
阅读本文你需具备知识点:
- 二叉查找树
- 完美平衡二叉树
正文
红黑树也是二叉查找树,我们知道,二叉查找树这一数据结构并不难,而红黑树之所以难是难在它是自平衡的二叉查找树,在进行插入和删除等可能会破坏树的平衡的操作时,需要重新自处理达到平衡状态。现在在脑海想下怎么实现?是不是太多情景需要考虑了?啧啧,先别急,通过本文的学习后,你会觉得,其实也不过如此而已。好吧,我们先来看下红黑树的定义和一些基本性质。
红黑树定义和性质
红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质:
- 性质1:每个节点要么是黑色,要么是红色。
- 性质2:根节点是黑色。
- 性质3:每个叶子节点(NIL)是黑色。
- 性质4:每个红色结点的两个子结点一定都是黑色。
- 性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
从性质5又可以推出:
- 性质5.1:如果一个结点存在黑子结点,那么该结点肯定有两个子结点
图1就是一颗简单的红黑树。其中Nil为叶子结点,并且它是黑色的。(值得提醒注意的是,在Java中,叶子结点是为null的结点。)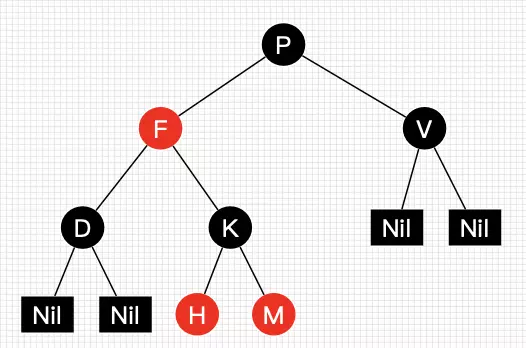
图1 一颗简单的红黑树
红黑树并不是一个完美平衡二叉查找树,从图1可以看到,根结点P的左子树显然比右子树高,但左子树和右子树的黑结点的层数是相等的,也即任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质5)。所以我们叫红黑树这种平衡为黑色完美平衡。
介绍到此,为了后面讲解不至于混淆,我们还需要来约定下红黑树一些结点的叫法,如图2所示。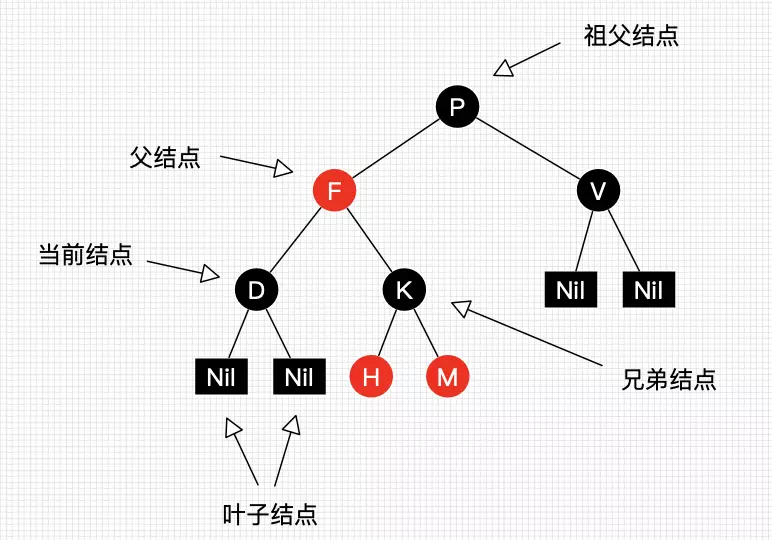
图2 结点叫法约定
我们把正在处理(遍历)的结点叫做当前结点,如图2中的D,它的父亲叫做父结点,它的父亲的另外一个子结点叫做兄弟结点,父亲的父亲叫做祖父结点。
前面讲到红黑树能自平衡,它靠的是什么?三种操作:左旋、右旋和变色。
- 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。如图3。
- 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。如图4。
- 变色:结点的颜色由红变黑或由黑变红。
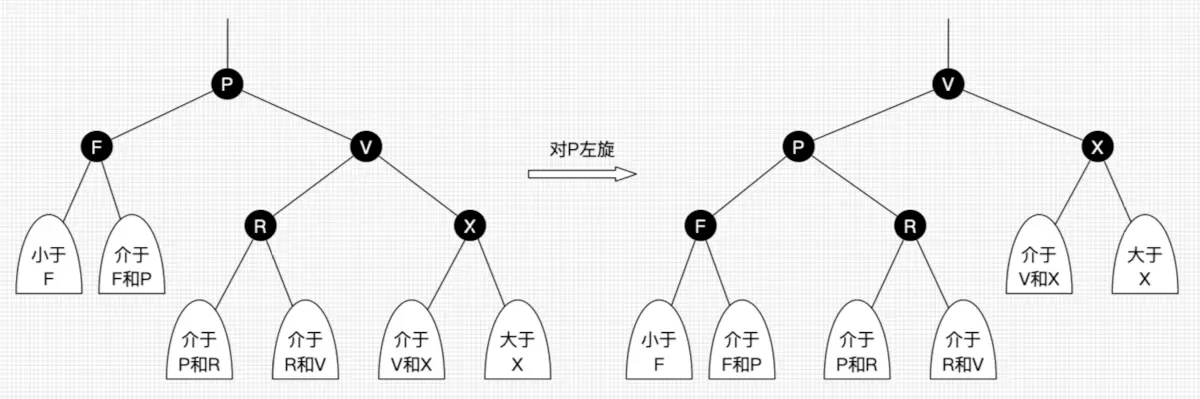
图3 左旋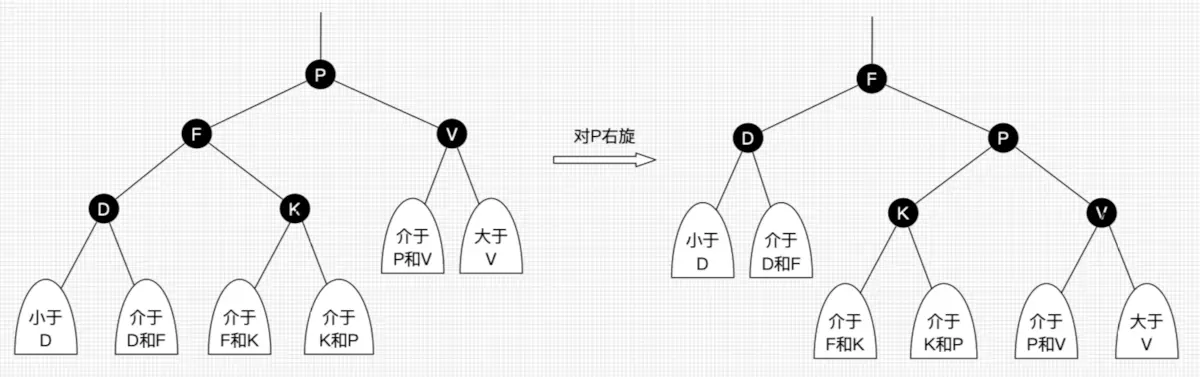
图4 右旋
上面所说的旋转结点也即旋转的支点,图4和图5中的P结点。
我们先忽略颜色,可以看到旋转操作不会影响旋转结点的父结点,父结点以上的结构还是保持不变的。
左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。
右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
所以旋转操作是局部的。另外可以看出旋转能保持红黑树平衡的一些端详了:当一边子树的结点少了,那么向另外一边子树“借”一些结点;当一边子树的结点多了,那么向另外一边子树“租”一些结点。
但要保持红黑树的性质,结点不能乱挪,还得靠变色了。怎么变?具体情景又不同变法,后面会具体讲到,现在只需要记住红黑树总是通过旋转和变色达到自平衡。
balabala了这么多,相信你对红黑树有一定印象了,那么现在来考考你:
思考题1:黑结点可以同时包含一个红子结点和一个黑子结点吗? (答案见文末)
接下来先讲解红黑树的查找热热身。
红黑树查找
因为红黑树是一颗二叉平衡树,并且查找不会破坏树的平衡,所以查找跟二叉平衡树的查找无异:
- 从根结点开始查找,把根结点设置为当前结点;
- 若当前结点为空,返回null;
- 若当前结点不为空,用当前结点的key跟查找key作比较;
- 若当前结点key等于查找key,那么该key就是查找目标,返回当前结点;
- 若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤2;
- 若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤2;
如图5所示。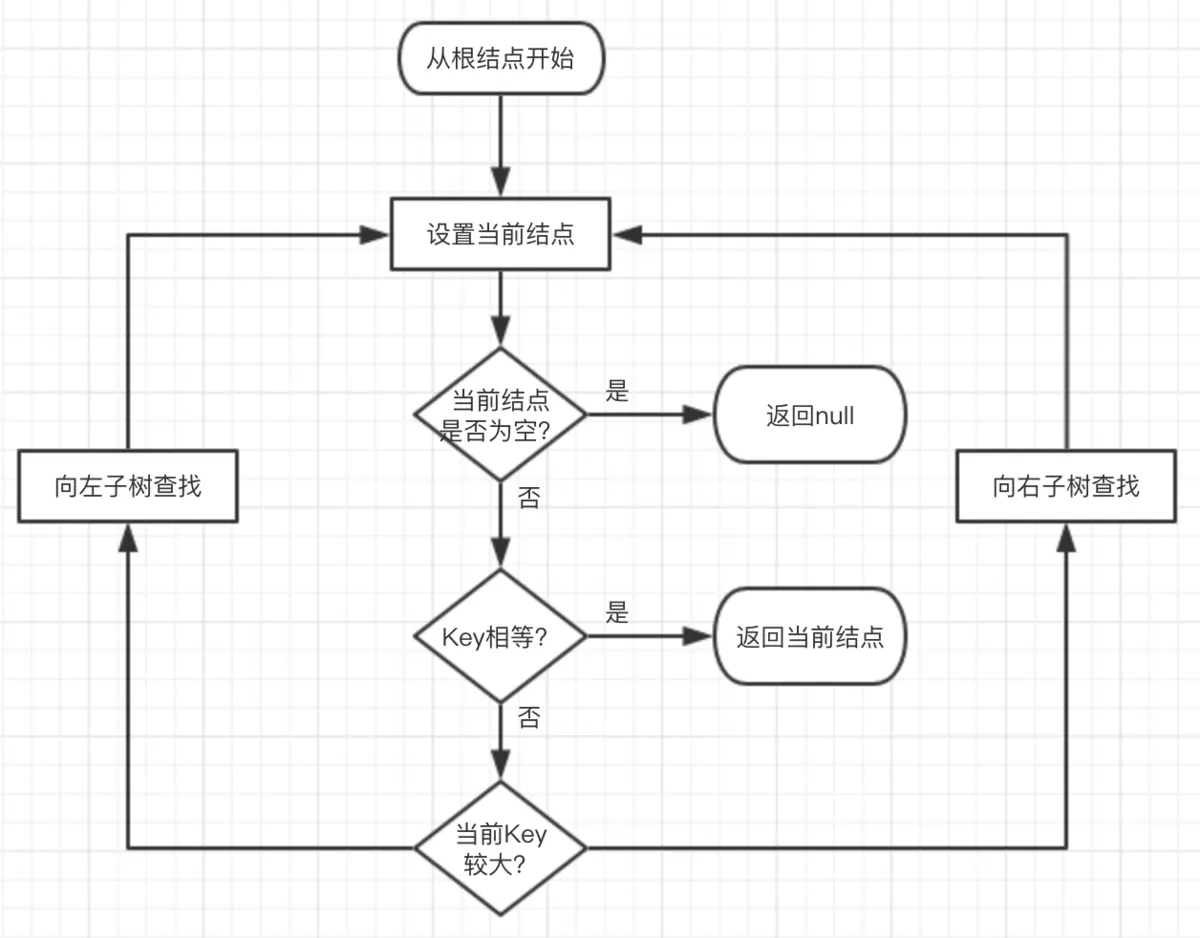
图5 二叉树查找流程图
非常简单,但简单不代表它效率不好。正由于红黑树总保持黑色完美平衡,所以它的查找最坏时间复杂度为O(2lgN),也即整颗树刚好红黑相隔的时候。能有这么好的查找效率得益于红黑树自平衡的特性,而这背后的付出,红黑树的插入操作功不可没~
红黑树插入
插入操作包括两部分工作:一查找插入的位置;二插入后自平衡。查找插入的父结点很简单,跟查找操作区别不大:
- 从根结点开始查找;
- 若根结点为空,那么插入结点作为根结点,结束。
- 若根结点不为空,那么把根结点作为当前结点;
- 若当前结点为null,返回当前结点的父结点,结束。
- 若当前结点key等于查找key,那么该key所在结点就是插入结点,更新结点的值,结束。
- 若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤4;
- 若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤4;
如图6所示。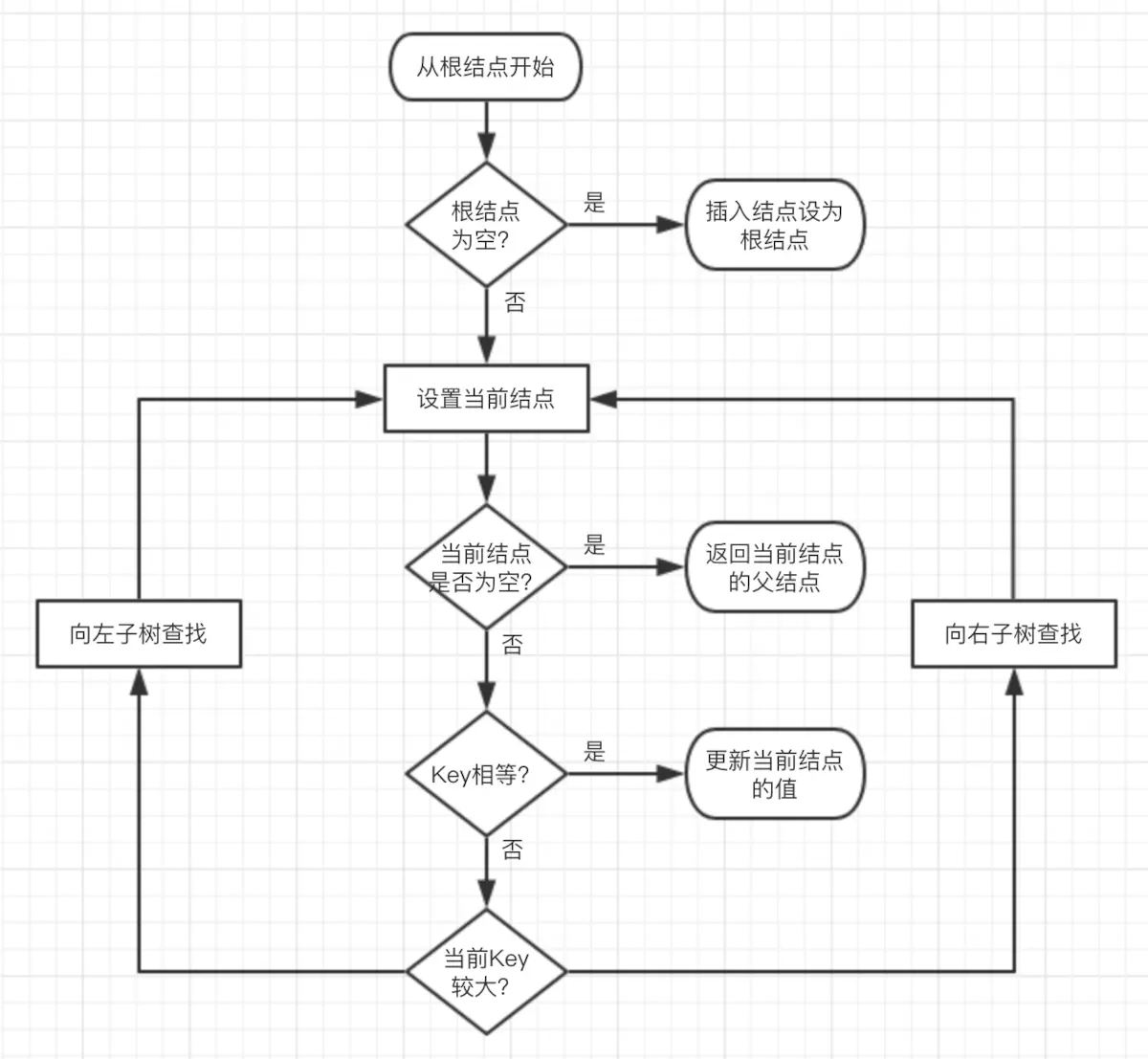
图6 红黑树插入位置查找
ok,插入位置已经找到,把插入结点放到正确的位置就可以啦,但插入结点是应该是什么颜色呢?答案是红色。理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
所有插入情景如图7所示。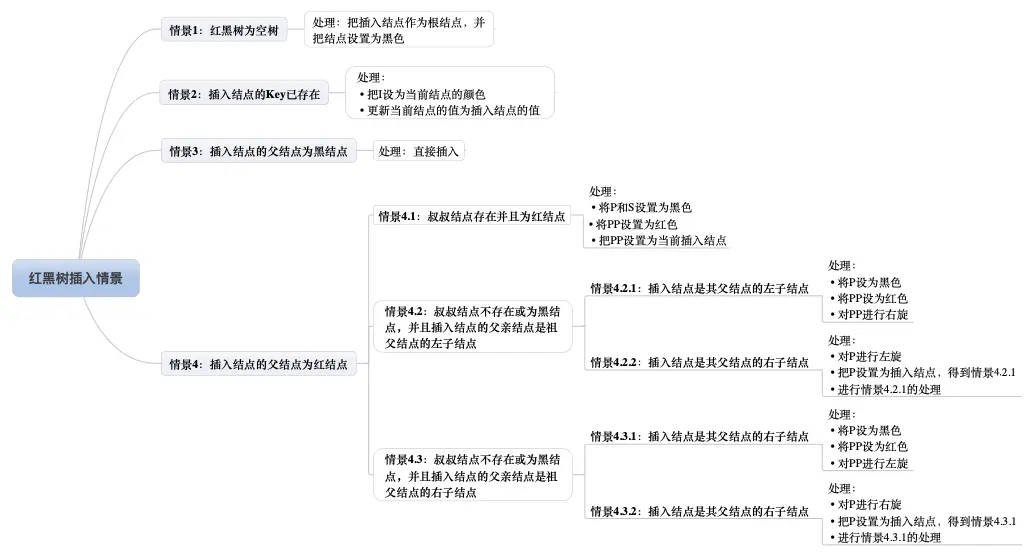
图7 红黑树插入情景
嗯,插入情景很多呢,8种插入情景!但情景1、2和3的处理很简单,而情景4.2和情景4.3只是方向反转而已,懂得了一种情景就能推出另外一种情景,所以总体来看,并不复杂,后续我们将一个一个情景来看,把它彻底搞懂。
另外,根据二叉树的性质,除了情景2,所有插入操作都是在叶子结点进行的。这点应该不难理解,因为查找插入位置时,我们就是在找子结点为空的父结点的。
在开始每个情景的讲解前,我们还是先来约定下,如图8所示。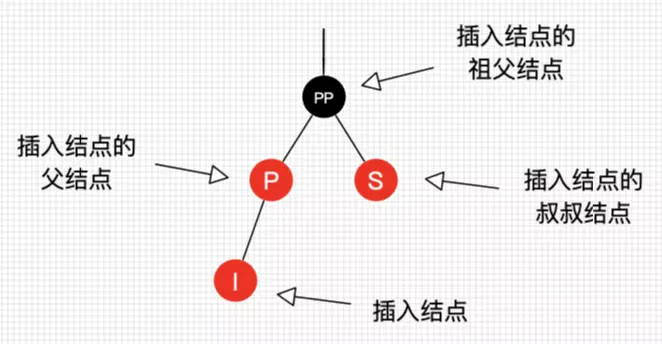
图8 插入操作结点的叫法约定
图8的字母并不代表结点Key的大小。I表示插入结点,P表示插入结点的父结点,S表示插入结点的叔叔结点,PP表示插入结点的祖父结点。
好了,下面让我们一个一个来分析每个插入的情景以其处理。
插入情景1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行,但注意,根据红黑树性质2:根节点是黑色。还需要把插入结点设为黑色。
处理:把插入结点作为根结点,并把结点设置为黑色。
插入情景2:插入结点的Key已存在
插入结点的Key已存在,既然红黑树总保持平衡,在插入前红黑树已经是平衡的,那么把插入结点设置为将要替代结点的颜色,再把结点的值更新就完成插入。
处理:
- 把I设为当前结点的颜色
-
插入情景3:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点的黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
处理:直接插入。插入情景4:插入结点的父结点为红结点
再次回想下红黑树的性质2:根结点是黑色。如果插入的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这点很重要,因为后续的旋转操作肯定需要祖父结点的参与。
情景4又分为很多子情景,下面将进入重点部分,各位看官请留神了。
插入情景4.1:叔叔结点存在并且为红结点
从红黑树性质4可以,祖父结点肯定为黑结点,因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红。如图9和图10所示。
处理: 将P和S设置为黑色
- 将PP设置为红色
- 把PP设置为当前插入结点

图9 插入情景4.1_1
图10 插入情景4.1_2
可以看到,我们把PP结点设为红色了,如果PP的父结点是黑色,那么无需再做任何处理;但如果PP的父结点是红色,根据性质4,此时红黑树已不平衡了,所以还需要把PP当作新的插入结点,继续做插入操作自平衡处理,直到平衡为止。
试想下PP刚好为根结点时,那么根据性质2,我们必须把PP重新设为黑色,那么树的红黑结构变为:黑黑红。换句话说,从根结点到叶子结点的路径中,黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。
我们还可以总结出另外一个经验:红黑树的生长是自底向上的。这点不同于普通的二叉查找树,普通的二叉查找树的生长是自顶向下的。
插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
单纯从插入前来看,也即不算情景4.1自底向上处理时的情况,叔叔结点非红即为叶子结点(Nil)。因为如果叔叔结点为黑结点,而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了,这不满足红黑树的性质5。后续情景同样如此,不再多做说明了。
前文说了,需要旋转操作时,肯定一边子树的结点多了或少了,需要租或借给另一边。插入显然是多的情况,那么把多的结点租给另一边子树就可以了。
插入情景4.2.1:插入结点是其父结点的左子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行右旋

图11 插入情景4.2.1
由图11可得,左边两个红结点,右边不存在,那么一边一个刚刚好,并且因为为红色,肯定不会破坏树的平衡。
咦,可以把P设为红色,I和PP设为黑色吗?答案是可以!看过《算法:第4版》的同学可能知道,书中讲解的就是把P设为红色,I和PP设为黑色。但把P设为红色,显然又会出现情景4.1的情况,需要自底向上处理,做多了无谓的操作,既然能自己消化就不要麻烦祖辈们啦~
插入情景4.2.2:插入结点是其父结点的右子结点
这种情景显然可以转换为情景4.2.1,如图12所示,不做过多说明了。
处理:
- 对P进行左旋
- 把P设置为插入结点,得到情景4.2.1
- 进行情景4.2.1的处理
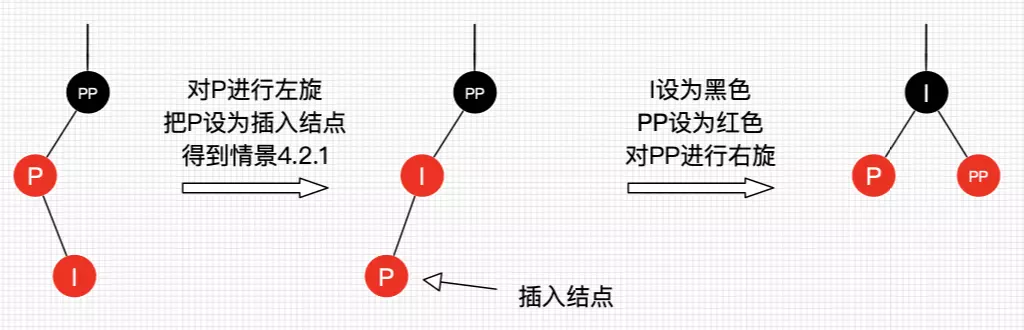
图12 插入情景4.2.2
插入情景4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景4.2,只是方向反转,不做过多说明了,直接看图。
插入情景4.3.1:插入结点是其父结点的右子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行左旋

图13 插入情景4.3.1
插入情景4.3.2:插入结点是其父结点的右子结点
处理:
- 对P进行右旋
- 把P设置为插入结点,得到情景4.3.1
- 进行情景4.3.1的处理
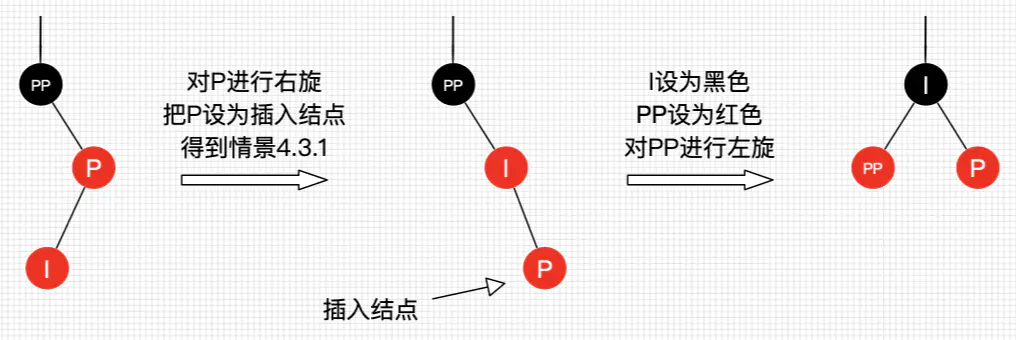
图14 插入情景4.3.2
好了,讲完插入的所有情景了。可能又同学会想:上面的情景举例的都是第一次插入而不包含自底向上处理的情况,那么上面所说的情景都适合自底向上的情况吗?答案是肯定的。理由很简单,但每棵子树都能自平衡,那么整棵树最终总是平衡的。好吧,在出个习题,请大家拿出笔和纸画下试试(请务必动手画下,加深印象):
习题1:请画出图15的插入自平衡处理过程。(答案见文末)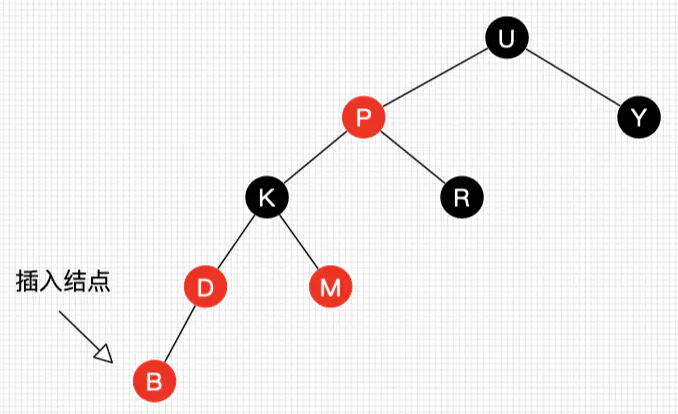
图15 习题1
红黑树删除
红黑树插入已经够复杂了,但删除更复杂,也是红黑树最复杂的操作了。但稳住,胜利的曙光就在前面了!
红黑树的删除操作也包括两部分工作:一查找目标结点;而删除后自平衡。查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;当存在目标结点时,删除后就得做自平衡处理了。删除了结点后我们还需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
二叉树删除结点找替代结点有3种情情景:
- 情景1:若删除结点无子结点,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点
补充说明下,情景3的后继结点是大于删除结点的最小结点,也是删除结点的右子树种最左结点。那么可以拿前继结点(删除结点的左子树最左结点)替代吗?可以的。但习惯上大多都是拿后继结点来替代,后文的讲解也是用后继结点来替代。另外告诉大家一种找前继和后继结点的直观的方法(不知为何没人提过,大家都知道?):把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点。如图16所示。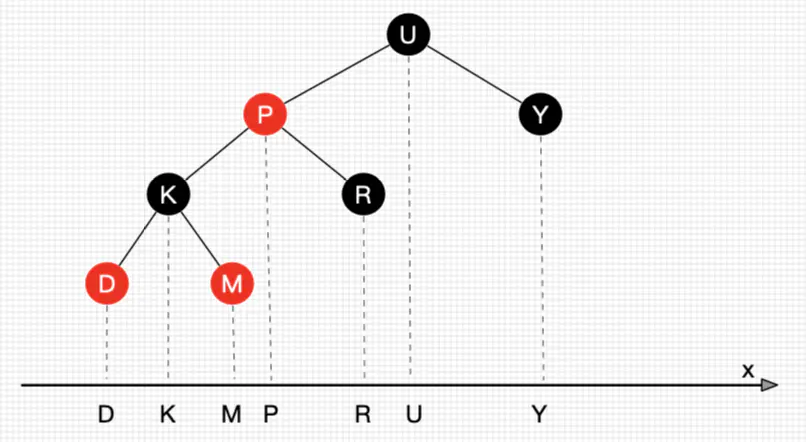
图16 二叉树投射x轴后有序
接下来,讲一个重要的思路:删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点!话很苍白,我们看图17。在不看键值对的情况下,图17的红黑树最终结果是删除了Q所在位置的结点!这种思路非常重要,大大简化了后文讲解红黑树删除的情景!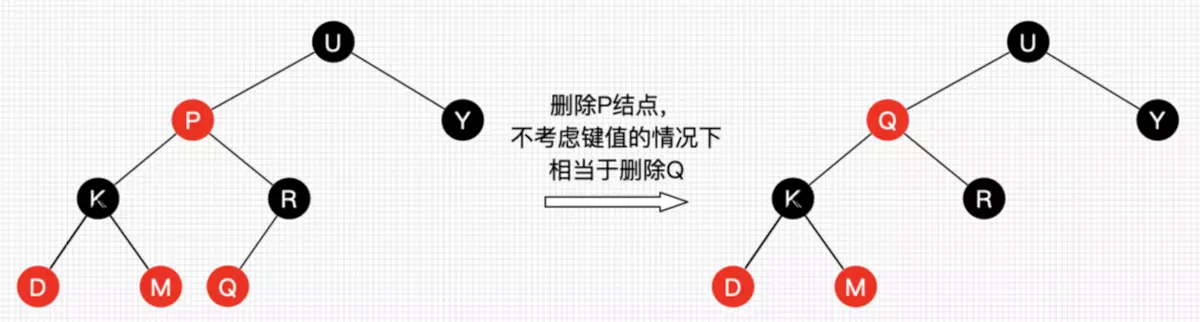
图17 删除结点换位思路
基于此,上面所说的3种二叉树的删除情景可以相互转换并且最终都是转换为情景1!
- 情景2:删除结点用其唯一的子结点替换,子结点替换为删除结点后,可以认为删除的是子结点,若子结点又有两个子结点,那么相当于转换为情景3,一直自顶向下转换,总是能转换为情景1。(对于红黑树来说,根据性质5.1,只存在一个子结点的结点肯定在树末了)
- 情景3:删除结点用后继结点(肯定不存在左结点),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1。
二叉树删除结点情景关系图如图18所示。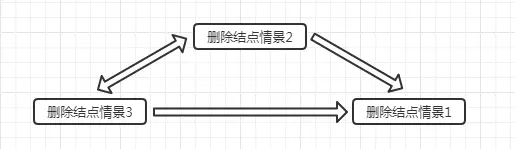
图18 二叉树删除情景转换
综上所述,删除操作删除的结点可以看作删除替代结点,而替代结点最后总是在树末。有了这结论,我们讨论的删除红黑树的情景就少了很多,因为我们只考虑删除树末结点的情景了。
同样的,我们也是先来总体看下删除操作的所有情景,如图19所示。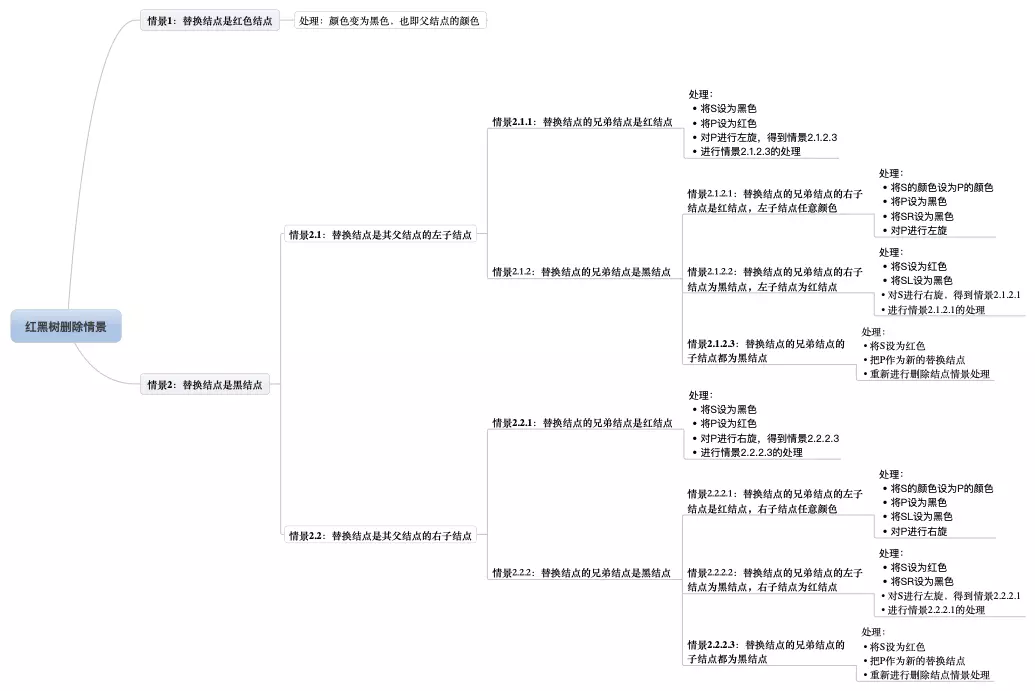
图19 红黑树删除情景
哈哈,是的,即使简化了还是有9种情景!但跟插入操作一样,存在左右对称的情景,只是方向变了,没有本质区别。同样的,我们还是来约定下,如图20所示。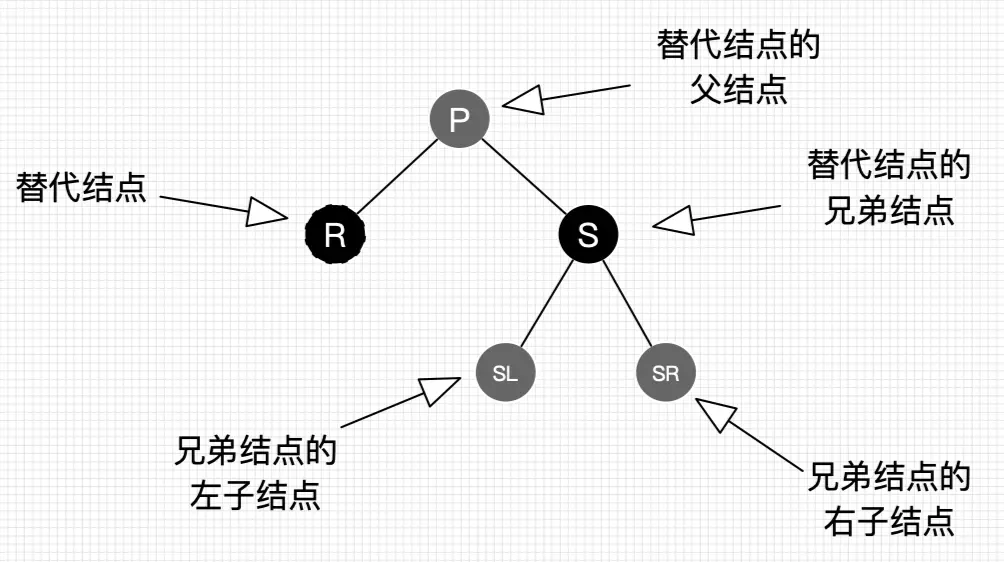
图20 删除操作结点的叫法约定
图20的字母并不代表结点Key的大小。R表示替代结点,P表示替代结点的父结点,S表示替代结点的兄弟结点,SL表示兄弟结点的左子结点,SR表示兄弟结点的右子结点。灰色结点表示它可以是红色也可以是黑色。
值得特别提醒的是,R是即将被替换到删除结点的位置的替代结点,在删除前,它还在原来所在位置参与树的子平衡,平衡后再替换到删除结点的位置,才算删除完成。
万事具备,我们进入最后的也是最难的讲解。
删除情景1:替换结点是红色结点
我们把替换结点换到了删除结点的位置时,由于替换结点时红色,删除也了不会影响红黑树的平衡,只要把替换结点的颜色设为删除的结点的颜色即可重新平衡。
处理:颜色变为删除结点的颜色
删除情景2:替换结点是黑结点
当替换结点是黑色时,我们就不得不进行自平衡处理了。我们必须还得考虑替换结点是其父结点的左子结点还是右子结点,来做不同的旋转操作,使树重新平衡。
删除情景2.1:替换结点是其父结点的左子结点
删除情景2.1.1:替换结点的兄弟结点是红结点
若兄弟结点是红结点,那么根据性质4,兄弟结点的父结点和子结点肯定为黑色,不会有其他子情景,我们按图21处理,得到删除情景2.1.2.3(后续讲解,这里先记住,此时R仍然是替代结点,它的新的兄弟结点SL和兄弟结点的子结点都是黑色)。
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行左旋,得到情景2.1.2.3
- 进行情景2.1.2.3的处理

图21 删除情景2.1.1
删除情景2.1.2:替换结点的兄弟结点是黑结点
当兄弟结点为黑时,其父结点和子结点的具体颜色也无法确定(如果也不考虑自底向上的情况,子结点非红即为叶子结点Nil,Nil结点为黑结点),此时又得考虑多种子情景。
删除情景2.1.2.1:替换结点的兄弟结点的右子结点是红结点,左子结点任意颜色
即将删除的左子树的一个黑色结点,显然左子树的黑色结点少1了,然而右子树又又红色结点,那么我们直接向右子树“借”个红结点来补充黑结点就好啦,此时肯定需要用旋转处理了。如图22所示。
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SR设为黑色
- 对P进行左旋

图22 删除情景2.1.2.1
平衡后的图怎么不满足红黑树的性质?前文提醒过,R是即将替换的,它还参与树的自平衡,平衡后再替换到删除结点的位置,所以R最终可以看作是删除的。另外图2.1.2.1是考虑到第一次替换和自底向上处理的情况,如果只考虑第一次替换的情况,根据红黑树性质,SL肯定是红色或为Nil,所以最终结果树是平衡的。如果是自底向上处理的情况,同样,每棵子树都保持平衡状态,最终整棵树肯定是平衡的。后续的情景同理,不做过多说明了。
删除情景2.1.2.2:替换结点的兄弟结点的右子结点为黑结点,左子结点为红结点
兄弟结点所在的子树有红结点,我们总是可以向兄弟子树借个红结点过来,显然该情景可以转换为情景2.1.2.1。图如23所示。
处理:
- 将S设为红色
- 将SL设为黑色
- 对S进行右旋,得到情景2.1.2.1
- 进行情景2.1.2.1的处理
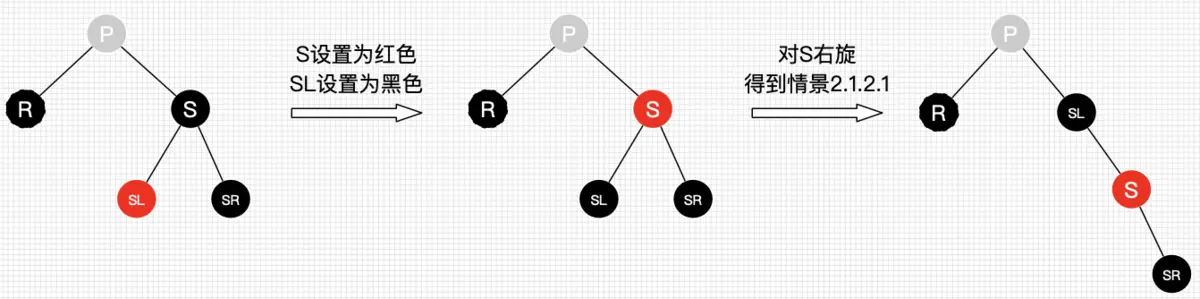
图23 删除情景2.1.2.2
删除情景2.1.2.3:替换结点的兄弟结点的子结点都为黑结点
好了,此次兄弟子树都没红结点“借”了,兄弟帮忙不了,找父母呗,这种情景我们把兄弟结点设为红色,再把父结点当作替代结点,自底向上处理,去找父结点的兄弟结点去“借”。但为什么需要把兄弟结点设为红色呢?显然是为了在P所在的子树中保证平衡(R即将删除,少了一个黑色结点,子树也需要少一个),后续的平衡工作交给父辈们考虑了,还是那句,当每棵子树都保持平衡时,最终整棵总是平衡的。
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理

图24 情景2.1.2.3
删除情景2.2:替换结点是其父结点的右子结点
好啦,右边的操作也是方向相反,不做过多说明了,相信理解了删除情景2.1后,肯定可以理解2.2。
删除情景2.2.1:替换结点的兄弟结点是红结点
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行右旋,得到情景2.2.2.3
- 进行情景2.2.2.3的处理

图25 删除情景2.2.1
删除情景2.2.2:替换结点的兄弟结点是黑结点
删除情景2.2.2.1:替换结点的兄弟结点的左子结点是红结点,右子结点任意颜色
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SL设为黑色
- 对P进行右旋

图26 删除情景2.2.2.1
删除情景2.2.2.2:替换结点的兄弟结点的左子结点为黑结点,右子结点为红结点
处理:
- 将S设为红色
- 将SR设为黑色
- 对S进行左旋,得到情景2.2.2.1
- 进行情景2.2.2.1的处理
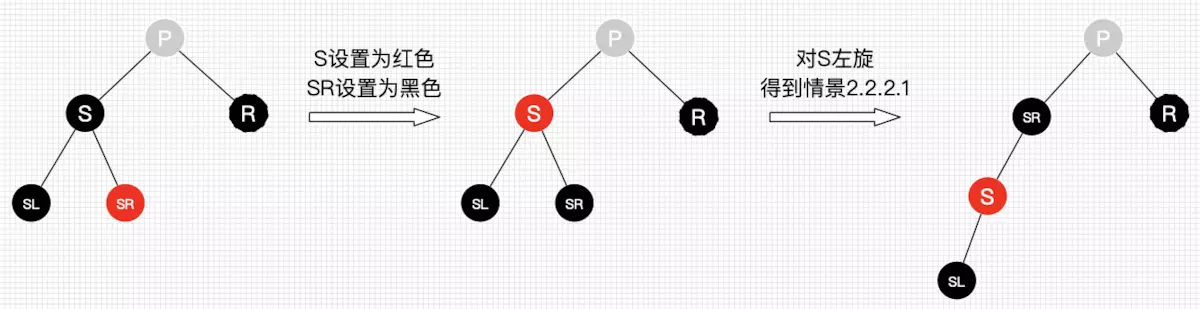
图27 删除情景2.2.2.2
删除情景2.2.2.3:替换结点的兄弟结点的子结点都为黑结点
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理
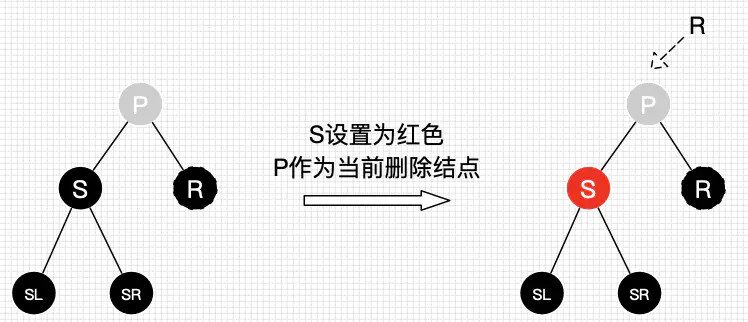
图28 删除情景2.2.2.3
综上,红黑树删除后自平衡的处理可以总结为:
- 自己能搞定的自消化(情景1)
- 自己不能搞定的叫兄弟帮忙(除了情景1、情景2.1.2.3和情景2.2.2.3)
- 兄弟都帮忙不了的,通过父母,找远方亲戚(情景2.1.2.3和情景2.2.2.3)
哈哈,是不是跟现实中很像,当我们有困难时,首先先自己解决,自己无力了总兄弟姐妹帮忙,如果连兄弟姐妹都帮不上,再去找远方的亲戚了。这里记忆应该会好记点~
最后再做个习题加深理解(请不熟悉的同学务必动手画下):
*习题2:请画出图29的删除自平衡处理过程。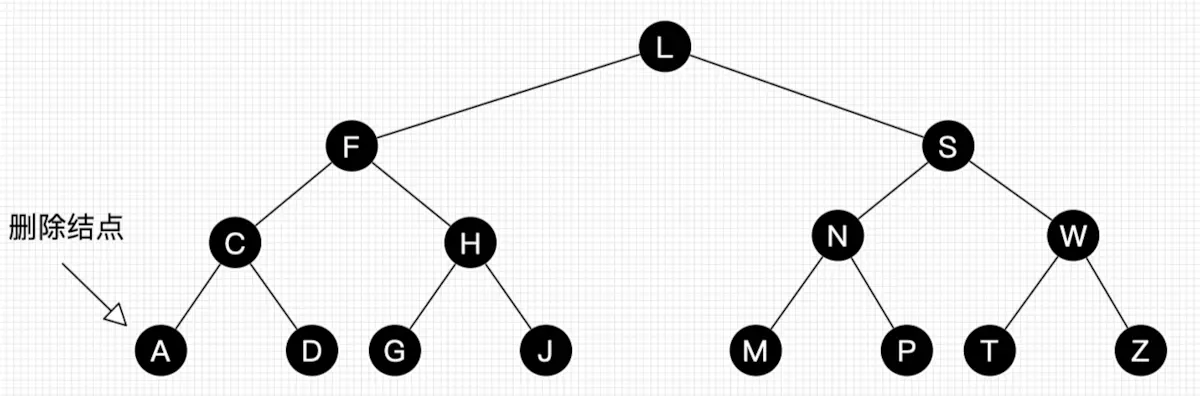
习题2
写在后面
耗时良久,终于写完了~自己加深了红黑树的理解的同时,也希望能帮助大家。如果你之前没学习过红黑树,看完这篇文章后可能还存在很多疑问,如果有疑问可以在评论区写出来,我会尽自己所能解答。另外给大家推荐一个支持红黑树在线生成的网站,来做各种情景梳理很有帮助:在线生成红黑树。(删除操作那个把替代结点看作删除结点思路就是我自己在用这个网站时自己顿悟的,我觉得这样讲解更容易理解。)
少了代码是不是觉得有点空虚?哈哈,后续我会写关于Java和HashMap和TreeMap的文章,里面都有红黑树相关的知识。相信看了这篇文章后,再去看Java和HashMap和TreeMap的源码绝对没难度!
原文地址:https://www.yuque.com/lobotomy/java/dsragh