[教程来源：Datawhale]

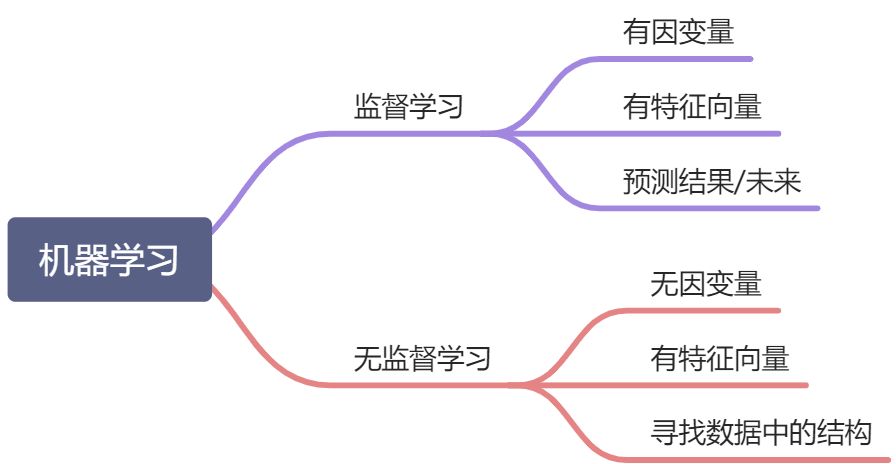
1.概览

• 什么是机器学习？

用数学模型去解释数据，发现数据中的规律，用做数据的预测与分析。

• 如何理解数据？

数据通常由一组向量组成，这组向量中的单个向量叫做样本。
我们通常用来表示样本，，共个样本；每个样本共有p+1个维度，前p个维度我们统称为一个特征（自变量），最后一个成为因变量。

• 机器学习按照是否有因变量，有无标注区分成监督学习和无监督学习。

1. 有监督学习：给定某些特征去估计因变量，即因变量存在的时候，我们称这个机器学习任务为有监督学习。如：我们使用房间面积，房屋所在地区，环境等级等因素去预测某个地区的房价。
2. 无监督学习：给定某些特征但不给定因变量，建模的目的是学习数据本身的结构和关系。如：我们给定某电商用户的基本信息和消费记录，通过观察数据中的哪些类型的用户彼此间的行为和属性类似，形成一个客群。注意，我们本身并不知道哪个用户属于哪个客群，即没有给定因变量。 根据因变量的是否连续，又分为回归和分类：

• 回归：因变量连续，如身高、体重；
• 分类：因变量离散，如西瓜的好坏。

为了更好地叙述后面的内容，我们对数据的形式作出如下约定：
第个样本：
因变量：
第k个特征：
特征矩阵：

在机器学习中，一般使用scikit-learn库工具库来探索机器学习项目。

1.1 回归

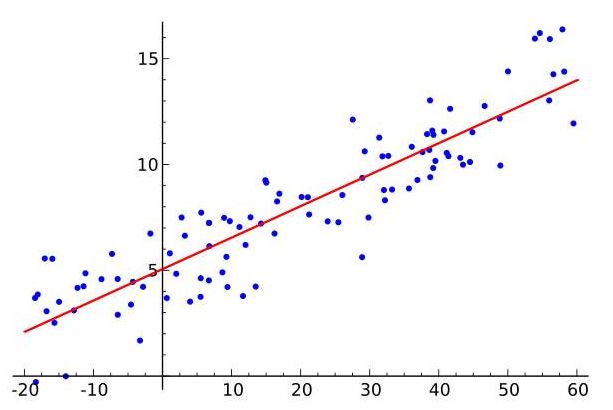
回归方法我们一般假设若干自变量与因变量有某种相关性，或者用一条线来描述一组向量的变化。
通俗理解：输出一个线性函数，例如

• 当实例只有一个属性时，输入输出之间关系就是二维平面的一条直线
• 当实例属性数目较多时，得到的是n+1维空间的一个超平面，对应一个维度等于于n的线性子空间

在学习的过程中，一般都是讨论单个自变量与因变量之间的关系，但是在实际的生产活动中，数据的维度是很多维度的，一般会选取相关性较高的一些变量和使用一些投影来解决“高维度灾难”。如计算皮尔逊系数，使用PCI方法进行降维等等。

在回归家族中，按变量的类型分为，单变量线性回归（如：）和多变量线性回归（）和多元线性回归()
按照用途可以分为，预测用途的常见回归和用于分类的逻辑回归。

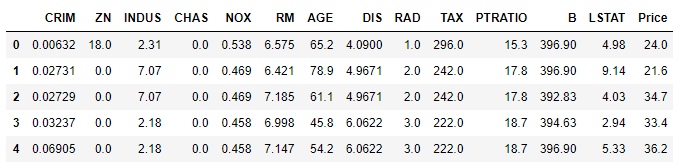
有监督学习中回归的例子，我们使用sklearn内置数据集Boston房价数据集。

import pandas as pd 
from sklearn import datasets
boston = datasets.load_boston()     # 加载数据集
X = boston.data
y = boston.target
features = boston.feature_names
boston_data = pd.DataFrame(X,columns=features)
boston_data["Price"] = y
boston_data.head()

import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(boston_data['NOX'],boston_data['Price'],color="r",alpha=0.6)
plt.title("Price~NOX")
plt.show()

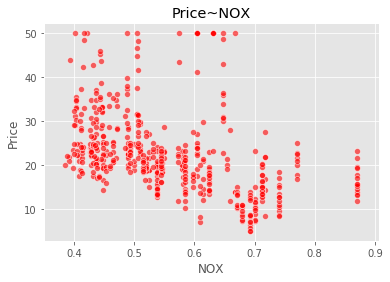
我们可以看到，数据给定任务所需要的因变量，因变量为波士顿房价Price是一个连续型变量，所以这是一个回归的例子。

NOX：一氧化氮浓度(/千万分之一)

from sklearn.linear_model import LinearRegression
line = LinearRegression()
X = boston_data[['NOX']]
y = boston_data['Price']
line.fit(X,y)
plt.scatter(boston_data['NOX'],boston_data['Price'],color="r",alpha=0.6)
plt.plot(boston_data['NOX'],line.predict(X),color="g",alpha=0.4,linewidth = 7.5)
plt.title("Price~NOX")
plt.show()

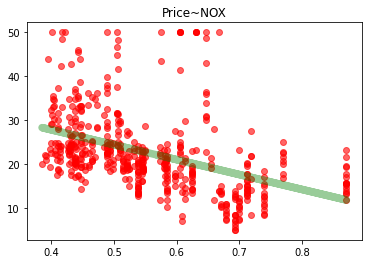
（红配绿好看）

1.2 分类

加载大名鼎鼎的花花数据集

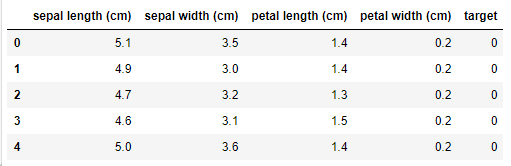
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
features = iris.feature_names
iris_data = pd.DataFrame(X,columns=features)
iris_data['target'] = y
iris_data.head()

import numpy as np
marker = ['s','x','o']
for index,c in enumerate(np.unique(y)):
    plt.scatter(x=iris_data.loc[y==c,"sepal length (cm)"],y=iris_data.loc[y==c,"sepal width (cm)"],alpha=0.8,label=c,marker=marker[c])
plt.xlabel("sepal length (cm)")
plt.ylabel("sepal width (cm)")
plt.legend()
plt.show()

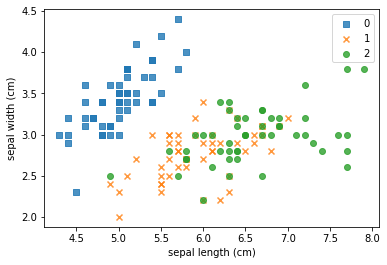
我们可以看到：每种不同的颜色和点的样式为一种类型的鸢尾花，数据集有三种不同类型的鸢尾花。因此因变量是一个类别变量，因此通过特征预测鸢尾花类别的问题是一个分类问题。

各个特征的相关解释：

• sepal length (cm)：花萼长度(厘米)
• sepal width (cm)：花萼宽度(厘米)
• petal length (cm)：花瓣长度(厘米)
• petal width (cm)：花瓣宽度(厘米)

分类用的少。

1.3 无监督学习

库中已经封装好的的数据集，详细API可以查看【传送门】

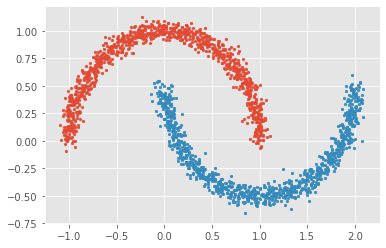
# 生成月牙型非凸集
from sklearn import datasets
x, y = datasets.make_moons(n_samples=2000, shuffle=True,
                  noise=0.05, random_state=None)
for index,c in enumerate(np.unique(y)):
    plt.scatter(x[y==c,0],x[y==c,1],s=7)
plt.show()

# 生成符合正态分布的聚类数据
from sklearn import datasets
x, y = datasets.make_blobs(n_samples=5000, n_features=2, centers=3)
for index,c in enumerate(np.unique(y)):
    plt.scatter(x[y==c, 0], x[y==c, 1],s=7)
plt.show()

这两个例子中，有个共同的特点就是没有标签。
无监督学习比较适合神经网络算法，本章内容为集成学习，不在后面继续讨论了。