本周练习内容:数据结构与算法 —— Tree
这些都是数据结构与算法,一部分方法是团队其他成员实现的,一部分我自己做的,有什么其他实现方法或错误,欢迎各位大佬指点,感谢。
一、什么是树?
1.树有什么特点,什么是二叉树和二叉搜索树(BST: Binary Search Tree)?
2.生活中常见的例子有哪些?
解析:
- 树有什么特点,什么是二叉树和二叉搜索树:
- 树是一种非线性的数据结构,以分层方式存储数据,用来表示有层级关系的数据。
- 每棵树至多只有一个根结点,根结点会有很多子节点,每个子节点只有一个父结点。
- 父结点和子节点是相对的。
- 生活中的例子:
如:家谱、公司组织架构图。
二、请实现二叉搜索树(BST),并实现以下方法:
insert(key):向树中插入一个新的键;search(key):树中查找一个键,如果节点存在返回true,不存在返回false;min():返回树中最小的值/键;max():返回树中最大的值/键;remove(key):移除某个键;
提示:所谓的键对应于之前章节所学的节点(Node)
class Node {constructor(key){this.key = keythis.left = nullthis.right = null}}class BST {constructor(){this.root = null}/*** 插入一个节点* @param {*} node 插入的位置节点* @param {*} newNode 插入的节点*/insertNode (node, newNode){if(newNode.key < node.key){if(node.left === null && node.right === null){node.left = newNode}else if(node.left !== null && node.right === null){node.right = newNode}else{this.insertNode(node.left, newNode)}}else{if(node.left === null && node.right === null){node.left = newNode}else if(node.left !== null && node.right === null){node.right = newNode}else{this.insertNode(node.right, newNode)}}}/*** 插入操作* @param {*} key*/insert (key){let newNode = new Node(key)if(this.root === null){this.root = newNode}else{this.insertNode(this.root, newNode)}}searchNode (node, key){if(node === null) return falseif(key < node.key){return this.searchNode(node.left, key)}else if(key > node.key){return this.searchNode(node.right, key)}else{return true}}/*** 搜索操作* @param {*} key*/search (key){return this.searchNode(this.root, key)}/*** 最小值的节点*/min (){let node = this.rootif(node === null) return nullwhile(node && node.left !== null){node = node.left}return node.key}/*** 最大值的节点*/max (){let node = this.rootif(node === null) return nullwhile(node && node.right !== null){node = node.right}return node.key}/*** 找到最小节点* @param {*} node*/findMinNode (node){if(node === null) return nullwhile(node && node.left !== null){node = node.left}return node}/*** 删除一个节点* @param {*} node* @param {*} key*/removeNode (node, key){if(node === null) return nullif(key < node.key){node.left = this.removeNode(node.left, key)return node}else if(key > node.key){node.right = this.removeNode(node.right, key)return node}else{// 1.叶节点if(node.left === null && node.right === null){node = nullreturn node}// 2.只有一个子节点if(node.left === null){node = node.rightreturn node}else if(node.right === null){node = node.left}// 3.有两个子节点let curNode = this.findMinNode(node.right)node.key = curNode.keynode.right = this.removeNode(node.right, curNode.key)return node}}/*** 删除一个节点* @param {*} key*/remove (key){if(this.root === null) return nullthis.root = this.removeNode(this.root, key)}}
三、基于题二实现二叉搜索树扩展以下方法:
preOrderTraverse(): 通过先序遍历方式遍历所有节点;inOrderTraverse(): 通过中序遍历方式遍历所有节点;postOrderTraverse(): 通过后序遍历方式遍历所有节点;
提示:
- 先序:先访问根节点,然后以同样方式访问左子树和右子树;(根==>左==>右)
输出 =》 11 7 5 3 6 9 8 10 15 13 12 14 20 18 25
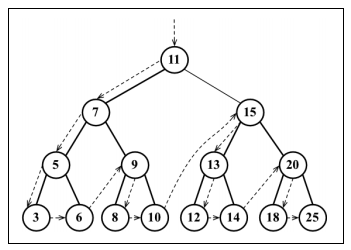
- 中序:先访问左子树,再访问根节点,最后访问右字数;以升序访问所有节点;(左==>根==>右)
输出 =》 3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
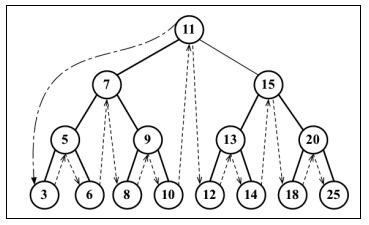
- 后序:先访问叶子节点,从左子树到右子树,再到根节点。(左==>右==>根)
输出 =》 3 6 5 8 10 9 7 12 14 13 18 25 20 15 11
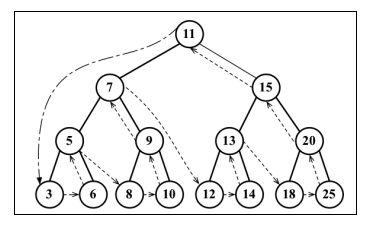
解析:
// 1. 先序BST.prototype.preOrderTraverseNode = function(node, callback){if(node !== null){callback(node.key)this.preOrderTraverseNode(node.left, callback)this.preOrderTraverseNode(node.right, callback)}}BST.prototype.preOrderTraverse = function(callback){this.preOrderTraverseNode(this.root, callback)}// 2. 中序BST.prototype.inOrderTraverseNode = function(node, callback){if(node !== null){this.inOrderTraverseNode(node.left, callback)callback(node.key)this.inOrderTraverseNode(node.right, callback)}}BST.prototype.inOrderTraverse = function(callback){this.inOrderTraverseNode(this.root, callback)}// 3. 后序BST.prototype.postOrderTraverseNode = function(node, callback){if(node !== null){this.postOrderTraverseNode(node.left, callback)this.postOrderTraverseNode(node.right, callback)callback(node.key)}}BST.prototype.postOrderTraverse = function(callback){this.postOrderTraverseNode(this.root, callback)}
四、请实现从上往下打印二叉树
给定的二叉树为:[3, 9 , 20, null, null, 15, 7]
3/ \9 20/ \15 7
请实现一个 printLevelOrder 方法,输出以下结果:
[[3],[9, 20],[15, 7]]
来源:102.二叉树的层次遍历
解析:
- 方法一:
BST.prototype.printLevelOrder = function (root, arr = [], i = 0){if (root && (root.key || root.key === 0)) {!arr[i] && (arr[i] = [])arr[i].push(root.key)i++root.left && this.printLevelOrder(root.left, arr, i)root.right && this.printLevelOrder(root.right, arr, i)}return arr}
- 方法二:
BST.prototype.printLevelOrder = function (){if(this.root === null) return []let result = [], queue = [this.root]while(true){let len = queue.length, arr = []while(len > 0){console.log(queue)let node = queue.shift()len -= 1arr.push(node.key)if(node.left !== null) queue.push(node.left)if(node.right !== null) queue.push(node.right)}if(arr.length === 0) return resultresult.push([...arr])}}
五、给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:2/ \1 3输出: true
示例 2:
输入:5/ \1 4/ \3 6输出: false解释: 输入为: [5,1,4,null,null,3,6]。根节点的值为 5 ,但是其右子节点值为 4 。
代码实现:
/*** 二叉树节点定义*/function TreeNode(val) {this.val = val;this.left = this.right = null;}/**- @param {TreeNode} root- @return {boolean}*/function isValidBST(root) {};
来源:99.验证二叉搜索树
解析:
function isValidBST(root) {let arr = []function inOrderTraverse(node){if(node === null) return;node.left && inOrderTraverse(node.left);arr.push(node.val);node.right && inOrderTraverse(node.right);}inOrderTraverse(root)for(let i = 0; i < arr.length - 1; i++){if(arr[i] >= arr[i+1]) return false}return true};
| Author | 王平安 |
|---|---|
| pingan8787@qq.com | |
| 博 客 | www.pingan8787.com |
| 微 信 | pingan8787 |
| 每日文章推荐 | https://github.com/pingan8787/Leo_Reading/issues |
| ES小册 | js.pingan8787.com |
微信公众号


