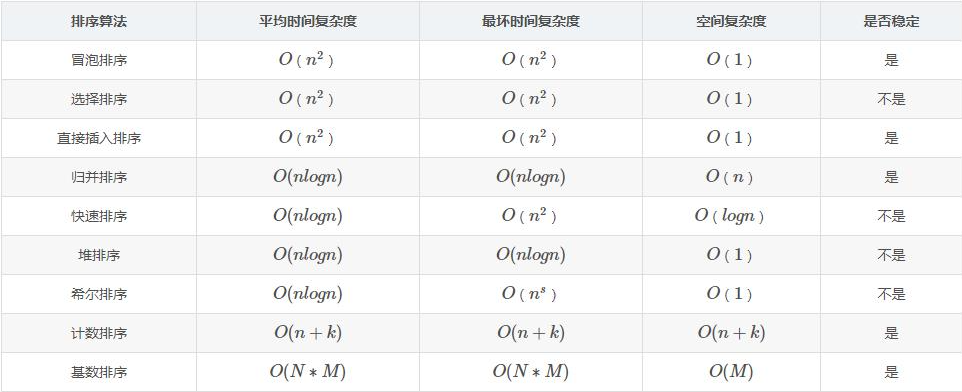
一、数据结构
数据结构是计算机存储、组织数据的方式。(数据结构是指数据与数据之间的关系。)
数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
1、逻辑结构
| 逻辑结构 | 示意图 |
|---|---|
| 1、集合结构 |  |
| 2、线性结构 |  |
| 3、树形结构 |  |
| 4、图形结构 |  |
2、存储结构
存储结构:保存在计算机里面的结构
| 存储结构 | 描述 |
|---|---|
| 1、数组 | 相同类型、若干变量、有序 |
| 2、散列表(哈希表) | 存储在f(key) |
| 3、链表 | 非连续、非顺序、链表指针(数据域,指针域) |
| 4、堆栈 | 先进后出 |
| 5、队列 | 先进先出 、后进后出 |
| 6、树 | 根、结点、叶子;前驱,后继;【e.g.】二叉树 |
| 7、图 | 结点(顶点)、边 |
二、算法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。(算法即解决问题的一套方法)
| 算法复杂度 | 描述 |
|---|---|
| 1、空间复杂度 | 运行时占用多少内存 |
| 2、时间复杂度 | 运行时占用多少时间,主要研究关键代码执行次数。表示:O(n) 。 【例】O(n) = n2 + 3n + 100 ==> O(n) = n2 【例】O(n) = n5 + n4 + n ==> O(n) = n5 |
【例1】
时间复杂度:O(n) = n2
for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {// TODO do something}}
【例2】
时间复杂度:O(n) = n2 + n + 1 ≈ n2
时间复杂度研究的是n => ∞,所以【例1】和【例2】的时间复杂度是一样的。所以我们考虑的是n的几次方的问题。
for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {// TODO do something}}for (int i = 0; i < n; i++) {// TODO do something}// TODO do something
O表示是时间复杂度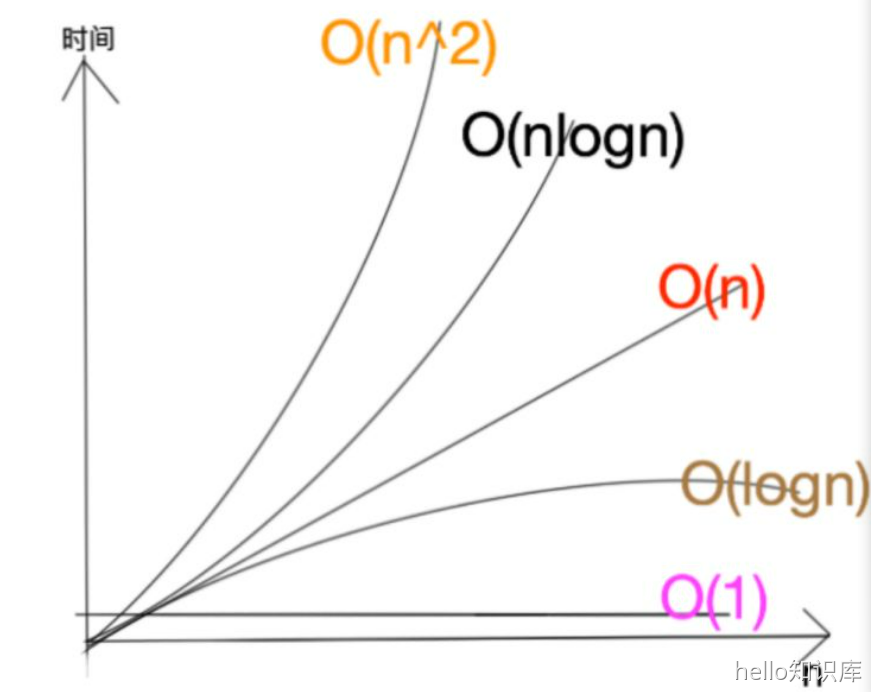
O(1)
最低的复杂度,无论数据量大小,耗时都不变,都可以在一次计算后获得。哈希算法就是典型的O(1)
O(n)
线性,n表示数据的量,当量增大,耗时也增大,常见有遍历算法
O(n²)
平方,表示耗时是n的平方倍,当看到循环嵌循环的时候,基本上这个算法就是平方级的,如:冒泡排序等
O(log n)
对数,通常ax=n,那么数x叫做以a为底n的对数,也就是x=logan,这里是a通常是2,如:数量增大8倍,耗时只增加了3倍,二分查找就是对数级的算法,每次剔除一半
O(n log n)
线性对数,就是n乘以log n,按照上面说的数据增大8倍,耗时就是8*3=24倍,归并排序就是线性对数级的算法
三、判定程序的好坏
程序 = 数据结构 + 算法
程序好坏 = 空间复杂度 + 时间复杂度 + 【应用场景】
【例1】swap (✔️)
定义一个临时变量实现两个数交换,可读性最好。【在不影响用户体验的情况下,选择可读性最好的程序】
public void swap() {int a = 5;int b = 6;int temp = a; // 定义一个临时变量a = b;b = temp;}
【例2】swap (×)
节省了一个空间,但是如果是对象,无法实现两个数交换。
public void swap() {int a = 5;int b = 6;a = a + b;b = a - b;a = a - b;}
【例3】swap (×)
执行速度最快,节省了一个空间,性能最优,支持对象交换,但是可读性差。适合对内存要求高,比如无人机,跑步机等
public void swap() {int a = 5;int b = 6;a = a ^ b;b = a ^ b;a = a ^ b;}