/ 写在前面 – 我热爱技术、热爱开源。我也相信开源能使技术变得更好、共享能使知识传播得更远。但是开源并不意味着某些商业机构/个人可以为了自身的利益而一味地索取，甚至直接剽窃大家曾为之辛勤付出的知识成果，所以本文未经允许，不得转载，谢谢。/

特殊矩阵

通用特殊矩阵

  • zeros 函数，产生全0矩阵。
  • ons 函数，产生全1矩阵。
  • eye 函数，产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。
  • rand 函数，产生(0,1)区间均匀分布的随机矩阵，不包括0和1。
  • randn 函数，产生均值为0，方差为1的标准正态分布随机矩阵，n代表normal，即正态分布。

这几个函数调用方法类似，以 zeros 为例：

  1. >> A=[1,2,3,4;5,6,7,8;9,10,11,12]
  2. A =
  3.      1     2     3     4
  4.      5     6     7     8
  5.      9    10    11    12
  6. >> size(A)
  7. ans =
  8.      3     4
  9. >> zeros(3)
  10. ans =
  11.      0     0     0
  12.      0     0     0
  13.      0     0     0
  14. >> zeros(3,4)
  15. ans =
  16.      0     0     0     0
  17.      0     0     0     0
  18.      0     0     0     0
  19. >> zeros(size(A))
  20. ans =
  21.      0     0     0     0
  22.      0     0     0     0
  23.      0     0     0     0

image.png
那么，要得到两位随机整数，即[10, 99]，故我们的取值范围就要在(10, 100)，可得下面的这个演化过程：

  1. (0, 1)
  2. (0, 1) * 90 = (0, 90)
  3. (0, 90) + 10 = (10, 100)
  4. 然后对(10, 100)进行 fix 取整即可

所以，我们可以通过上面这个过程，看到 a = 10, b = 99 ，故 b - a + 1 = 90 。

  1. >> A=fix(10+90*rand(5));
  2. >> B=0.6+sqrt(0.1)*randn(5);
  3. >> I=eye(5);
  4. >> (A+B)*I==I*A+B*I
  5. ans =
  6.   5×5 logical array
  7.    1   1   1   1   1
  8.    1   1   1   1   1
  9.    1   1   1   1   1
  10.    1   1   1   1   1
  11.    1   1   1   1   1

用于专门学科的特殊矩阵

魔方矩阵 - Magic Square

使用 magic 函数产生魔方矩阵：

  1. >> M=magic(3)
  2. M =
  3.      8     1     6
  4.      3     5     7
  5.      4     9     2

范德蒙矩阵 - Vandermonde Matrix

在MATLAB中，函数 vander(V) 生成以向量 V 为基础的范德蒙矩阵：

  1. >> A=vander(1:5)
  2. A =
  3.      1     1     1     1     1
  4.     16     8     4     2     1
  5.     81    27     9     3     1
  6.    256    64    16     4     1
  7.    625   125    25     5     1

范德蒙矩阵常用在各种通信系统的纠错编码中，例如，常用的Reed-Solomon编码即以范德蒙矩阵为基础。

希尔伯特矩阵 - Hilbert Matrix

希尔伯特矩阵的元素为MATLAB矩阵处理 - 图2。

在MATLAB中，生成n阶Hilbert Matrix的函数是 hilb(n) ：

  1. >> format rat% 设置输出格式为以有理数形式输出
  2. >> H=hilb(4)
  3. H =
  4.        1              1/2            1/3            1/4     
  5.        1/2            1/3            1/4            1/5     
  6.        1/3            1/4            1/5            1/6     
  7.        1/4            1/5            1/6            1/7

希尔伯特矩阵是著名的病态矩阵，即任何一个元素发生较小的变动，整个矩阵的值和逆矩阵都会发生很大的变化，病态程度和矩阵的阶数相关，随着阶数的增加，病态更加严重。

伴随矩阵 - Adjugate Matrix

MATLAB生成伴随矩阵的函数是 compan(p) ，其中 p 是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。

例如，生成多项式MATLAB矩阵处理 - 图3的伴随矩阵：

  1. >> p=[1,-2,-5,6];
  2. >> A=compan(p)
  3. A =
  4.      2     5    -6
  5.      1     0     0
  6.      0     1     0

伴随矩阵的特征值等于多项式方程的根。

帕斯卡矩阵 - Pascal Matrix

根据二项式定理，MATLAB矩阵处理 - 图4展开后的系数随着n的增大组成一个三角形表，这个三角形称为杨辉三角形。

把二项式系数依次填写在矩阵的左侧对角线上，然后提取左侧的n行n列元素即为n阶帕斯卡矩阵。

函数 pascal(n) 可以生成一个n阶帕斯卡矩阵。

矩阵变换

对角阵

几个定义：

  • 对角矩阵：只有对角线上有非零元素的矩阵。
  • 数量矩阵：对角线上的元素相等的对角矩阵。
  • 单位矩阵：对角线上的元素都为1的对角矩阵。

提取矩阵的对角线元素：

  • diag(A) ：提取矩阵A主对角线元素，产生一个列向量。
  • diag(A,k) ：提取矩阵A第k条对角线的元素，产生一个列向量。

关于矩阵对角线的条数的定义见下图：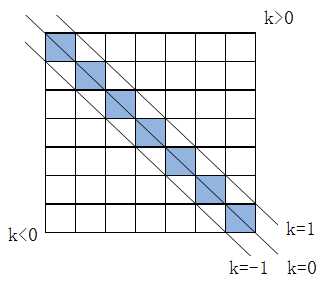
image.png
构造对角矩阵：

  • diag(V) ：以向量 V 为主对角线元素，产生对角矩阵。
  • diag(V,k) ：以向量 V 为第k条对角线元素，产生对角矩阵。

三角阵

几个定义：

  • 上三角阵：矩阵的对角线以下的元素全为0的矩阵。
  • 下三角阵：对角线以上的元素全为0的矩阵。

triu 函数用来求上三角矩阵，其中的u代表up，该函数有2种调用形式：

  • triu(A) ：提取矩阵A的主对角线及以上的元素。
  • triu(A,k) ：提取矩阵A的第k条对角线及以上的元素。

tril 函数用来求下三角矩阵，其中的l代表low，该函数有2种调用形式，与 triu 函数完全相同。

矩阵的转置

转置运算符是小数点后面接单引号 .' 。

还有一种转置是共轭转置，其运算符是单引号 ' ，它在转置的基础上还要取每个数的复共轭。

如果A是一个复数矩阵，那么转置运算和共轭转置的结果是不一样的。如果矩阵的元素是实数，那么转置和共轭转置的结果是一样的。

  1. >> A=[1,2;3,4]
  2. A =
  3.      1     2
  4.      3     4
  5. >> A.'
  6. ans =
  7.      1     3
  8.      2     4

矩阵的旋转

函数 rot90(A,k) 将矩阵A逆时针方向旋转90°的k倍，当k为1时可省略。

矩阵的翻转

对矩阵实施左右翻转，是将原矩阵的第一列和最后一列调换，第二列和倒数第二列调换，依次类推。

函数 fliplr(A) 可以对矩阵A实施左右翻转。

同理 ，我们还可以对矩阵实施上下翻转，其函数为 flipud(A) 。

矩阵求逆

函数 inv(A) 可以求方阵A的逆矩阵，前提是它有逆矩阵。
image.png

矩阵求值

矩阵的行列式值（Determinant）

如果矩阵MATLAB矩阵处理 - 图7是方形矩阵，则MATLAB矩阵处理 - 图8代表矩阵MATLAB矩阵处理 - 图9的行列式值。

函数 det(A) 可以求方阵A所对应的行列式的值。

矩阵的秩（Rank）

矩阵线性无关的行数或列数称为矩阵的秩。

函数 rank(A) 可以求矩阵A的秩。

矩阵的迹（Trace）

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。

函数 trace(A) 可以求矩阵A的迹。

向量和矩阵的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。范数有多种定义，其定义不同，范数的值也就不同。

向量的3种常用范数：

  1. 向量1-范数：向量元素的绝对值之和。

MATLAB矩阵处理 - 图10

  1. 向量2-范数：向量元素绝对值的平方和的平方根。

MATLAB矩阵处理 - 图11

  1. 向量∞-范数：所有向量元素绝对值种的最大值。

MATLAB矩阵处理 - 图12

在MATLAB种，求向量范数的函数为：

  1. norm(V) 或 norm(V,2) ：计算向量V的2-范数。
  2. norm(V,1) ：计算向量V的1-范数。
  3. norm(V,inf) ：计算向量V的∞-范数。

矩阵的范数：

  1. 矩阵A的1-范数：所有矩阵列元素绝对值之和的最大值。

MATLAB矩阵处理 - 图13

  1. 矩阵A的2-范数：MATLAB矩阵处理 - 图14矩阵的最大特征值的平方根。

MATLAB矩阵处理 - 图15
其中MATLAB矩阵处理 - 图16为MATLAB矩阵处理 - 图17的最大特征值。

  1. 矩阵A的∞-范数：所有矩阵行元素绝对值之和的最大值。

MATLAB矩阵处理 - 图18

MATLAB提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同。

矩阵的条件数

矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积。

条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差。

在MATLAB中，计算矩阵A的3种条件数的函数是：

  1. cond(A,1) ：计算A的1-范数下的条件数。
  2. cond(A) 或 cond(A,2) ：计算A的2-范数下的条件数。
  3. cond(A,inf) ：计算A的∞-范数下的条件数。

矩阵的特征值与特征向量

矩阵特征值的数学定义：设A是n阶方阵，如果存在常数λ和n维非零列向量x，使得等式MATLAB矩阵处理 - 图19成立，则称λ为A的特征值，x是对应特征值λ的特征向量

函数调用格式有2种：

  1. E=eig(A) ：求矩阵A的全部特征值，构成向量E。
  2. [X,D]=eig(A) ：求矩阵A的全部特征值，构成对角阵D，并产生矩阵X，X各列是相应的特征向量。

矩阵的特征值和特征向量是线性代数理论中的重要概念，在科学研究与工程实践中，有很广泛的应用，许多实际问题的求解最终归结为求矩阵的特征值与特征向量，如工程中的振动问题、动力系统的稳定性问题等。

稀疏矩阵

稀疏矩阵是指零元素的个数远远多于非零元素的个数的矩阵。MATLAB为稀疏矩阵提供了方便有效的存储方式。

在MATLAB中，矩阵的存储方式有：

  1. 完全存储方式：将矩阵的全部元素按列存储。
  2. 稀疏存储方式：只存储矩阵的非零元素的值及其位置，即行号和列号。

注意,采用稀疏存储方式时，矩阵元素的存储顺序并没有改变，也是按列的顺序进行存储。

完全存储方式与稀疏存储方式之间的转化

  1. A=sparse(S) ：将矩阵S转化为稀疏存储方式的矩阵A。
  2. S=full(A) ：将矩阵A转换为完全存储方式的矩阵S。

直接建立稀疏存储矩阵

对于超大的稀疏矩阵，先建立完全存储方式的矩阵，然后再进行转化是不可取的，所以MATLAB提供了直接建立稀疏存储矩阵的方式：

  1. sparse(m,n) ：生成一个m×n的所有元素都是0的稀疏矩阵。
  2. sparse(u,v,S) ：其中u、v、S是3个等长的向量。S是要建立的稀疏存储矩阵的非零元素， u(i) 、 v(i) 分别是 S(i) 的行和列下标。

使用 spconvert 函数直接建立稀疏存储矩阵，其调用格式为： B=spconvert(A) ，其中A为一个m×3或m×4的矩阵，其每行表示一个非零元素，m是非零元素的个数。

  • A(i,1) 表示第i个非零元素所在的行。
  • A(i,2) 表示第i个非零元素所在的列。
  • A(i,3) 表示第i个非零元素值的实部。
  • A(i,4) 表示第i个非零元素值的虚部。

若矩阵的全部元素都是实数，则无须第4列。

带状稀疏矩阵的稀疏存储

稀疏矩阵有两种基本类型：

  • 无规则结构的稀疏矩阵
  • 有规则结构的稀疏矩阵

带状稀疏矩阵就是一种十分典型的具有规则结构的稀疏矩阵，它是指所有非零元素集中在对角线上的矩阵。所以有：

  • [B,d]=spdiags(A) ：从带状稀疏矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d。
  • A=spdiags(B,d,m,n) ：产生带状稀疏矩阵的稀疏存储矩阵A，其中m、n为原带状稀疏矩阵的行数与列数，矩阵B的第i列即为原带状稀疏矩阵的第i条非零对角线，向量d为原带状稀疏矩阵所有非零对角线的位置。
  1. >> A=[11,0,0,12,0,0;0,21,0,0,22,0;0,0,31,0,0,32;41,0,0,42,0,0;0,51,0,0,52,0]
  2. A =
  3.     11     0     0    12     0     0
  4.      0    21     0     0    22     0
  5.      0     0    31     0     0    32
  6.     41     0     0    42     0     0
  7.      0    51     0     0    52     0
  8. >> [B,d]=spdiags(A)
  9. B =
  10.      0    11    12
  11.      0    21    22
  12.      0    31    32
  13.     41    42     0
  14.     51    52     0
  15. d =
  16.     -3
  17.      0
  18.      3

单位矩阵的稀疏存储

speye(m,n) 返回一个m×n的稀疏存储单位矩阵。