S06P01-概率图

概率图

概率图是一类用图的形式表示随机变量之间条件依赖关系的概率模型， 是概率论与图论的结合。图中的节点表示随机变量，缺少边表示条件独立假设。根据图中边的有向、无向性，模型可分为两类：有向图、无向图

贝叶斯网络

对于随机变量，根据贝叶斯公式有链式法则

%3DP(x1)%5Cprod%7Bi%3D2%7D%5EdP(xi%7Cx_1%2C%5Ccdots%2Cx%7Bi-1%7D)%0A#card=math&code=P%28x1%2Cx_2%2C%5Ccdots%2Cx_d%29%3DP%28x_1%29%5Cprod%7Bi%3D2%7D%5EdP%28xi%7Cx_1%2C%5Ccdots%2Cx%7Bi-1%7D%29%0A)

如果根据链式法则去计算的联合概率分布，计算量和参数量都十分巨大，因此我们作出一些假设来简化计算
最简单的假设就是假设都相互独立，但是这个假设太强，因此发展出马尔科夫假设，即下一个随机变量只与上一个随机变量有关，与其他随机变量相互独立，表示为。进一步可以将某些随机变量纳入一个集合，比如这些变量组成三个互不相交的集合，可以假设，这就是条件独立性假设
用有向图表示条件概率的规则：对#card=math&code=P%28x_j%7Cx_i%29)，那么在有向图中为的父节点。根据刚才的马尔科夫条件独立性假设，在一个个节点的有向图中，所有随机变量的联合概率表示为因子分解的形式，这种概率图称为贝叶斯网络

%3D%5Cprod%7Bi%3D1%7D%5EpP(x_i%7Cx%7Bpa(i)%7D)%0A#card=math&code=P%28x1%2Cx_2%2C%5Ccdots%2Cx_p%29%3D%5Cprod%7Bi%3D1%7D%5EpP%28xi%7Cx%7Bpa%28i%29%7D%29%0A)

其中%7D#card=math&code=x_%7Bpa%28i%29%7D)表示的父节点，一个节点可能会有多个父节点
例如如下的贝叶斯网络，D代表考试难度，I代表学生智力水平，G代表考试成绩，S代表SAT成绩，L代表推荐信，那么联合概率分布为

%3DP(D)P(I)P(S%7CI)P(G%7CD%2CI)P(L%7CG)%0A#card=math&code=P%28D%2CI%2CG%2CS%2CL%29%3DP%28D%29P%28I%29P%28S%7CI%29P%28G%7CD%2CI%29P%28L%7CG%29%0A)

基本结构

从图中可以看出对于有向图来说一般有以下三种基本结构

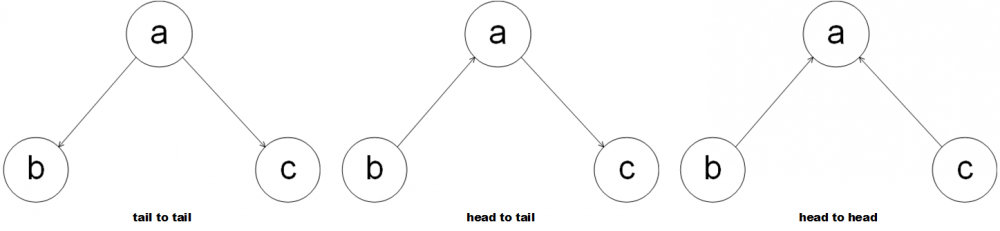
1. tail to tail
   根据因子分解%3DP(a)P(b%7Ca)P(c%7Ca)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28a%29P%28b%7Ca%29P%28c%7Ca%29)，根据链式法则%3DP(a)P(b%7Ca)P(c%7Ca%2Cb)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28a%29P%28b%7Ca%29P%28c%7Ca%2Cb%29)，令二者相等即P(b%7Ca)P(c%7Ca)%3DP(a)P(b%7Ca)P(c%7Ca%2Cb)%5C%5C%0A%5CRightarrow%20P(c%7Ca)%3DP(c%7Ca%2Cb)%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%7Ca%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AP%28a%29P%28b%7Ca%29P%28c%7Ca%29%3DP%28a%29P%28b%7Ca%29P%28c%7Ca%2Cb%29%5C%5C%0A%5CRightarrow%20P%28c%7Ca%29%3DP%28c%7Ca%2Cb%29%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%7Ca%0A%5Cend%7Bgathered%7D%0A)

因此在tail-tail的拓扑结构中，若a被观测，则路径阻塞，b和c相互独立
结合示例，对于I,G,S节点：如果一个学生SAT成绩好，那么你有理由认为他的考试分数高，因为SAT成绩好意味着智力水平高，因此在没有观测的情况下S和G不独立；但是如果已经观测到学生的智力水平高，那么无论他SAT成绩好或坏你都可以推断他的考试分数高，如果他的SAT成绩差可能是因为他发挥失常了，但是SAT成绩对考试分数的推断没有影响，所以在观测到I时S和G独立

1. head to tail
   根据因子分解%3DP(b)P(a%7Cb)P(c%7Ca)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28b%29P%28a%7Cb%29P%28c%7Ca%29)，根据链式法则%3DP(b)P(a%7Cb)P(c%7Ca%2Cb)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28b%29P%28a%7Cb%29P%28c%7Ca%2Cb%29)，令二者相等即P(a%7Cb)P(c%7Ca)%3DP(b)P(a%7Cb)P(c%7Ca%2Cb)%5C%5C%0A%5CRightarrow%20P(c%7Ca)%3DP(c%7Ca%2Cb)%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%7Ca%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AP%28b%29P%28a%7Cb%29P%28c%7Ca%29%3DP%28b%29P%28a%7Cb%29P%28c%7Ca%2Cb%29%5C%5C%0A%5CRightarrow%20P%28c%7Ca%29%3DP%28c%7Ca%2Cb%29%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%7Ca%0A%5Cend%7Bgathered%7D%0A)

因此在head-tail的拓扑结构中，若a被观测，则路径阻塞，b和c相互独立
结合示例，对于D,G,L节点：如果考试的难度大，那么学生拿到推荐信的概率就小，因为考试很难意味着很难拿高分，所以在没有观测的情况下D和L不独立；但是如果已经观测到考试分数高，那么拿到推荐信的概率就很高，与考试难度无关，所以在观测到G时D和L独立

1. head to head
   根据因子分解%3DP(a%7Cb%2Cc)P(b)P(c)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28a%7Cb%2Cc%29P%28b%29P%28c%29)，根据链式法则%3DP(b)P(c%7Cb)P(a%7Cb%2Cc)#card=math&code=P%28a%2Cb%2Cc%29%3DP%28b%29P%28c%7Cb%29P%28a%7Cb%2Cc%29)，令二者相等即P(b)P(c)%3DP(b)P(c%7Cb)P(a%7Cb%2Cc)%5C%5C%0A%5CRightarrow%20P(c)%3DP(c%7Cb)%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AP%28a%7Cb%2Cc%29P%28b%29P%28c%29%3DP%28b%29P%28c%7Cb%29P%28a%7Cb%2Cc%29%5C%5C%0A%5CRightarrow%20P%28c%29%3DP%28c%7Cb%29%5C%5C%0A%5CRightarrow%20c%5Cbot%20b%0A%5Cend%7Bgathered%7D%0A)

因此在head-head的拓扑结构中，b和c是天然相互独立的，反而在a被观测时b和c相关。这种结构一般被称为V形结构
结合示例，对于D,I,G节点：没有任何观测的情况下，显然考试难度和学生智力水平是完全独立的；但是在观测到考试分数高时，如果考试难度大，那么我们可以推测学生智力水平高，同样观测到考试分数低时，如果考试难度简单我们推断学生智力水平低，所以在观测到G时D和I不独立

D-Seperation

上述的讨论是对单一节点的讨论，如何推广到这样的随机变量集合上呢，如下图

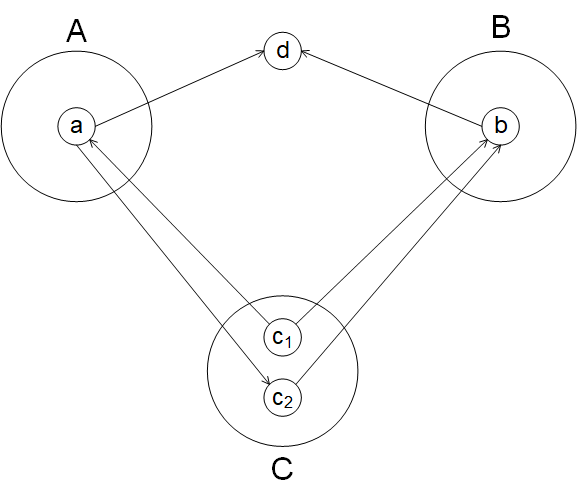很显然，只要集合A中任意节点a到集合B中任意节点b的迹中，所有tail-tail、head-tail结构的节点c都在集合C中，所有V字结构的节点d都不在C中，那么根据之前的讨论可得。这种规则又称为全局马尔可夫性

马尔科夫随机场

贝叶斯网络对应的图是有向无环图，其实用无向图也可以表示联合概率分布，这种用无向图的方式称为概率无向图，又叫马尔科夫随机场

定义

给定一个联合概率分布#card=math&code=P%28x_1%2Cx_2%2C%5Ccdots%2Cx_p%29)和表示他它的无向图，定义无向图表示的随机变量之间存在成对马尔可夫性、局部马尔可夫性和全局马尔可夫性

• 成对马尔可夫性：设是无向图G中没有边连接的节点，成对马尔可夫性是指在给定除了以外的其他所有随机变量的条件下和是条件独立的%3DP(xi%7Cx%7B-ij%7D)P(xj%7Cx%7B-ij%7D)%0A#card=math&code=P%28xi%2Cx_j%7Cx%7B-ij%7D%29%3DP%28xi%7Cx%7B-ij%7D%29P%28xj%7Cx%7B-ij%7D%29%0A)

• 局部马尔可夫性：设与有边相连接的所有节点集合为，是除以外所有节点的集合，局部马尔可夫性是指在给定的条件下与是条件独立的%3DP(x_i%7CW)P(O%7CW)%0A#card=math&code=P%28x_i%2CO%7CW%29%3DP%28x_i%7CW%29P%28O%7CW%29%0A)

• 全局马尔可夫性：设节点集合是被节点集合分开的任意节点集合，全局马尔可夫性是指在给定的条件下和是条件独立的%3DP(A%7CC)P(B%7CC)%0A#card=math&code=P%28A%2CB%7CC%29%3DP%28A%7CC%29P%28B%7CC%29%0A)

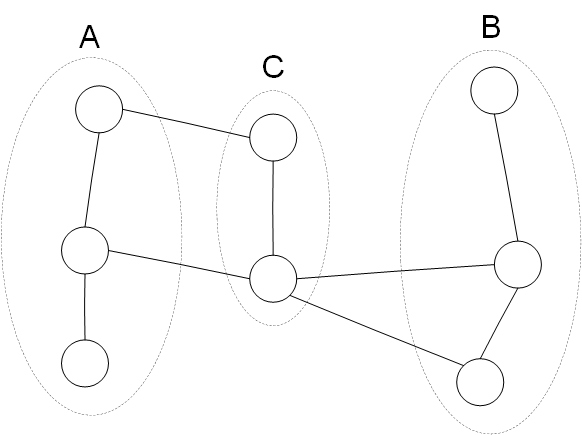
如果一个联合概率分布的无向图表示满足以上成对马尔可夫性、局部马尔可夫性和全局马尔可夫性，那么称这个联合概率分布为马尔科夫随机场。实际上成对马尔可夫性、局部马尔可夫性和全局马尔可夫性是等价的，数学上可以证明

因子分解

与贝叶斯网络类似，在马尔科夫随机场中我们也希望把联合概率分布写成因子分解的形式

• 团与最大团：无向图中任意两个节点均有边连接的节点子集称为团。若一个团不能再加进任何一个节点使其成为一个更大的团，则称其为最大团
• 马尔科夫随机场的因子分解：联合概率分布表示为其最大团上的随机变量的函数的乘积的形式，称为概率无向图的因子分解
  设概率无向图G中有p个节点，C为G上的最大团，最大团对应的随机变量集合为，则联合概率分布可写为%3D%7B1%5Cover%20Z%7D%5Cprod_C%5Cphi_C(x_C)%0A#card=math&code=P%28x_1%2Cx_2%2C%5Ccdots%2Cx_p%29%3D%7B1%5Cover%20Z%7D%5Cprod_C%5Cphi_C%28x_C%29%0A)

其中称为规范化因子，保证构成一个概率分布%3D%5Csum%7Bx_1%7D%5Csum%7Bx2%7D%5Ccdots%5Csum%7Bxp%7D%5Cprod_C%5Cphi_C(x_C)%0A#card=math&code=Z%3D%5Csum%7Bx%3Dx1%2Cx_2%2C%5Ccdots%2Cx_p%7D%5Cprod_C%5Cphi_C%28x_C%29%3D%5Csum%7Bx1%7D%5Csum%7Bx2%7D%5Ccdots%5Csum%7Bx_p%7D%5Cprod_C%5Cphi_C%28x_C%29%0A)

#card=math&code=%5Cphi_C%28x_C%29)称为势函数，要求严格为正，因此常用指数函数%3D%5Cexp%5B-E(x_C)%5D#card=math&code=%5Cphi_C%28x_C%29%3D%5Cexp%5B-E%28x_C%29%5D)，其中#card=math&code=E%28x%29)为能量函数，此时#card=math&code=P%28x_1%2Cx_2%2C%5Ccdots%2Cx_p%29)称为Boltzman Dsitribution

Hammersley-Clifford定理：一个概率无向图的联合概率分布表示为因子分解的形式等价于满足成对马尔可夫性、局部马尔可夫性和全局马尔可夫性

道德图

对于贝叶斯网络这种有向图，我们往往希望能够转换成无向图。下面讨论具体方法，还是从三种基本结构入手

1. tail-tail%3DP(a)P(b%7Ca)P(c%7Ca)%0A#card=math&code=P%28a%2Cb%2Cc%29%3DP%28a%29P%28b%7Ca%29P%28c%7Ca%29%0A)

如果要变为无向图，那么联合概率应该写成最大团的势函数形式。显然在这个基本结构中，有两个最大团和，可以令%3DP(a)P(b%7Ca)#card=math&code=%5Cphi%7Bab%7D%28a%2Cb%29%3DP%28a%29P%28b%7Ca%29)，令%3DP(c%7Ca)#card=math&code=%5Cphi%7Bac%7D%28a%2Cc%29%3DP%28c%7Ca%29)，，于是就写为%3D%5Cfrac%7B%5Cphi%7Bab%7D(a%2Cb)%5Cphi%7Bac%7D(a%2Cc)%7D%7BZ%7D%0A#card=math&code=P%28a%2Cb%2Cc%29%3D%5Cfrac%7B%5Cphi%7Bab%7D%28a%2Cb%29%5Cphi_%7Bac%7D%28a%2Cc%29%7D%7BZ%7D%0A)

此时把有向边变为无向边即可转化为无向图

1. head-tail
   同理令%3DP(b)P(a%7Cb)#card=math&code=%5Cphi%7Bab%7D%28a%2Cb%29%3DP%28b%29P%28a%7Cb%29)，令%3DP(c%7Ca)#card=math&code=%5Cphi%7Bac%7D%28a%2Cb%29%3DP%28c%7Ca%29)，%3D%5Cfrac%7B%5Cphi%7Bab%7D(a%2Cb)%5Cphi%7Bac%7D(a%2Cc)%7D%7BZ%7D%0A#card=math&code=P%28a%2Cb%2Cc%29%3D%5Cfrac%7B%5Cphi%7Bab%7D%28a%2Cb%29%5Cphi_%7Bac%7D%28a%2Cc%29%7D%7BZ%7D%0A)

把有向边变为无向边即可转化为无向图

1. head-head%3DP(b)P(c)P(a%7Cb%2Cc)%0A#card=math&code=P%28a%2Cb%2Cc%29%3DP%28b%29P%28c%29P%28a%7Cb%2Cc%29%0A)

此时要变为无向图只能将三个变量放在一个最大团内，于是令%3DP(b)P(c)P(a%7Cb%2Cc)#card=math&code=%5Cphi%7Babc%7D%28a%2Cb%2Cc%29%3DP%28b%29P%28c%29P%28a%7Cb%2Cc%29)，%3D%5Cfrac%7B%5Cphi%7Babc%7D(a%2Cb%2Cc)%7D%7BZ%7D%0A#card=math&code=P%28a%2Cb%2Cc%29%3D%5Cfrac%7B%5Cphi_%7Babc%7D%28a%2Cb%2Cc%29%7D%7BZ%7D%0A)

转化后的无向图为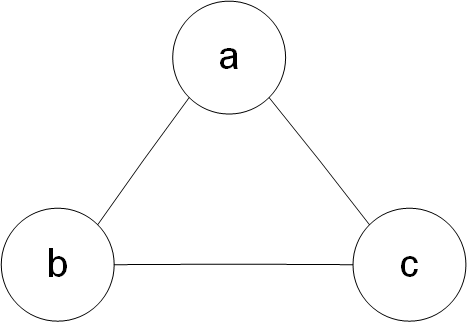

任意有向图转化为无向图的规则：对有向图任意节点，将其父节点两两相连，再将图中所有有向边替换为无向边即转化为了无向图。这样转化出来的无向图称为该有向图的道德图
数学上可以证明，有向图的全局马尔可夫性与其道德图的全局马尔可夫性等价