EM算法

EM算法是用于含隐变量的概率模型参数极大似然估计或极大后验估计的方法。在概率模型不仅含有观测变量(observed variable)，还含有隐变量(latent variable)时，简单的极大似然估计或者极大后验估计不可行，这时就需要EM算法

三硬币模型

问题

假设有三个硬币A,B,C，其正面向上的概率分别为a,b,c。有如下实验：做两步投掷，第一步先掷硬币A；第二步如果上一步出现正面则掷硬币B，如果上一步出现反面则掷硬币C，最终得到正面记为1，反面记为0。把这个两步实验做n次，得到一个实验结果序列。要求不看掷硬币的过程，仅根据实验结果推断a,b,c的值

解决方法

显然这个问题中含有一个隐变量，即掷硬币A的结果，或者第二步是掷硬币B还是硬币C，这个变量是我们没法观测到的，一般记隐变量为S06P02-EM算法 - 图1。记最后结果为S06P02-EM算法 - 图2，令S06P02-EM算法 - 图3#card=math&code=%5Ctheta%3D%28a%2Cb%2Cc%29)为模型参数，于是可以把这个问题写为

S06P02-EM算法 - 图4%26%3D%5Csum_ZP(y%2CZ%7C%5Ctheta)%3D%5Csum_ZP(y%7C%5Ctheta%2CZ)P(Z%7C%5Ctheta)%5C%5C%0A%26%3Dab%5Ey(1-b)%5E%7B1-y%7D%2B(1-a)c%5Ey(1-c)%5E%7B1-y%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28y%7C%5Ctheta%29%26%3D%5Csum_ZP%28y%2CZ%7C%5Ctheta%29%3D%5Csum_ZP%28y%7C%5Ctheta%2CZ%29P%28Z%7C%5Ctheta%29%5C%5C%0A%26%3Dab%5Ey%281-b%29%5E%7B1-y%7D%2B%281-a%29c%5Ey%281-c%29%5E%7B1-y%7D%0A%5Cend%7Baligned%7D%0A)

如果做了n次实验，得到的样本为S06P02-EM算法 - 图5#card=math&code=Y%3D%28y_1%2Cy_2%2C%5Ccdots%2Cy_n%29)，根据极大似然估计，则要极大化下式

S06P02-EM算法 - 图6%26%3D%5Cprod%7Bi%3D1%7D%5EnP(y_i%7C%5Ctheta)%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5En%5Bab%5E%7Byi%7D(1-b)%5E%7B1-y_i%7D%2B(1-a)c%5E%7By_i%7D(1-c)%5E%7B1-y_i%7D%5D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28Y%7C%5Ctheta%29%26%3D%5Cprod%7Bi%3D1%7D%5EnP%28yi%7C%5Ctheta%29%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5En%5Bab%5E%7By_i%7D%281-b%29%5E%7B1-y_i%7D%2B%281-a%29c%5E%7By_i%7D%281-c%29%5E%7B1-y_i%7D%5D%0A%5Cend%7Baligned%7D%0A)

这个问题是没有解析解的，只能通过迭代的方法求解。EM算法就是解决这种问题的一种迭代方法

EM算法推导

给定观测样本S06P02-EM算法 - 图7#card=math&code=X%3D%28X_1%2CX_2%2C%5Ccdots%2CX_N%29)，其对应的隐变量为S06P02-EM算法 - 图8。于是可写出对应的对数似然函数

S06P02-EM算法 - 图9%3D%5Clog%20P(X%7C%5Ctheta)%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P(X_i%7C%5Ctheta)%0A#card=math&code=L%28%5Ctheta%29%3D%5Clog%20P%28X%7C%5Ctheta%29%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P%28X_i%7C%5Ctheta%29%0A)

ELBO和KL散度

对S06P02-EM算法 - 图10#card=math&code=L%28%5Ctheta%29)做一些变换

S06P02-EM算法 - 图11%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP(Z%7CX_i%2C%5Ctheta)%7D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5B%5Clog%20P(Xi%2CZ%7C%5Ctheta)-%5Clog%20P(Z%7CX_i%2C%5Ctheta)%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5B%5Clog%5Cfrac%7BP(Xi%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7D-%5Clog%5Cfrac%7BP(Z%7CX_i%2C%5Ctheta)%7D%7BP_i(Z)%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cfrac%7BP%28Xi%2CZ%7C%5Ctheta%29%7D%7BP%28Z%7CX_i%2C%5Ctheta%29%7D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5B%5Clog%20P%28Xi%2CZ%7C%5Ctheta%29-%5Clog%20P%28Z%7CX_i%2C%5Ctheta%29%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5B%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D-%5Clog%5Cfrac%7BP%28Z%7CX_i%2C%5Ctheta%29%7D%7BP_i%28Z%29%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A)

其中S06P02-EM算法 - 图12#card=math&code=P_i%28Z%29)为对每一个样本引入的一个概率分布，满足S06P02-EM算法 - 图13dZ%3D1#card=math&code=%5Cint_ZP_i%28Z%29dZ%3D1)。上式两边的每一个S06P02-EM算法 - 图14对应的项对S06P02-EM算法 - 图15#card=math&code=P_i%28Z%29)求期望

S06P02-EM算法 - 图16%5Clog%20P(X_i%7C%5Ctheta)dZ%5C%5C%0A%26%3D%5Clog%20P(X_i%7C%5Ctheta)%5Cint_ZP_i(Z)dZ%5C%5C%0A%26%3D%5Clog%20P(X_i%7C%5Ctheta)%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%5Cbegin%7Baligned%7D%0Aright_i%3D%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ-%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(Z%7CX_i%2C%5Ctheta)%7D%7BP_i(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cbegin%7Baligned%7D%0Aleft_i%26%3D%5Cint_ZP_i%28Z%29%5Clog%20P%28X_i%7C%5Ctheta%29dZ%5C%5C%0A%26%3D%5Clog%20P%28X_i%7C%5Ctheta%29%5Cint_ZP_i%28Z%29dZ%5C%5C%0A%26%3D%5Clog%20P%28X_i%7C%5Ctheta%29%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%5Cbegin%7Baligned%7D%0Aright_i%3D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ-%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28Z%7CX_i%2C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A)

对右边部分，定义一个Evidence Lower Bound

S06P02-EM算法 - 图17%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ%0A#card=math&code=ELBO_i%3D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%0A)

显然有

S06P02-EM算法 - 图18%7C%7CP(Z%7CX_i%2C%5Ctheta))%26%3D%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP_i(Z)%7D%7BP(Z%7CX_i%2C%5Ctheta)%7DdZ%5C%5C%0A%26%3D-%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(Z%7CX_i%2C%5Ctheta)%7D%7BP_i(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AKL%28P_i%28Z%29%7C%7CP%28Z%7CX_i%2C%5Ctheta%29%29%26%3D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP_i%28Z%29%7D%7BP%28Z%7CX_i%2C%5Ctheta%29%7DdZ%5C%5C%0A%26%3D-%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28Z%7CX_i%2C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A)

则可得

S06P02-EM算法 - 图19%7C%7CP(Z%7CX_i%2C%5Ctheta))%5C%5C%0A%26%5Cge%20ELBO_i%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Aright_i%26%3DELBO_i%2BKL%28P_i%28Z%29%7C%7CP%28Z%7CX_i%2C%5Ctheta%29%29%5C%5C%0A%26%5Cge%20ELBO_i%0A%5Cend%7Baligned%7D%0A)

等号当且仅当S06P02-EM算法 - 图20%3DP(Z%7CX_i%2C%5Ctheta)#card=math&code=P_i%28Z%29%3DP%28Z%7CX_i%2C%5Ctheta%29)时成立
求和以后最终写为

S06P02-EM算法 - 图21%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P(X_i%7C%5Ctheta)%5C%5C%0A%26%5Cge%20%5Csum%7Bi%3D1%7D%5EN%5CintZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P%28Xi%7C%5Ctheta%29%5C%5C%0A%26%5Cge%20%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A)

上式表明说S06P02-EM算法 - 图22#card=math&code=L%28%5Ctheta%29)有一个下界，下界由S06P02-EM算法 - 图23#card=math&code=P_i%28Z%29)决定，极大化这个下界就相当于在极大化S06P02-EM算法 - 图24#card=math&code=L%28%5Ctheta%29)。显然在取等号的时候极大化下界等价于极大化S06P02-EM算法 - 图25#card=math&code=L%28%5Ctheta%29)，于是在第S06P02-EM算法 - 图26次迭代对于S06P02-EM算法 - 图27%7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D)，令S06P02-EM算法 - 图28%3DP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)#card=math&code=P_i%28Z%29%3DP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29)等号成立，即用S06P02-EM算法 - 图29关于给定S06P02-EM算法 - 图30%7D#card=math&code=X_i%2C%5Ctheta%5E%7B%28t%29%7D)的后验概率来估计它，可以令

S06P02-EM算法 - 图31%7D)%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%7DdZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5B%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ-%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)dZ%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ-%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)dZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AB%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%7DdZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5B%5CintZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ-%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29dZ%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ-%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29dZ%0A%5Cend%7Baligned%7D%0A)

在第S06P02-EM算法 - 图32轮迭代时，S06P02-EM算法 - 图33%7D)#card=math&code=B%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29)在S06P02-EM算法 - 图34%7D#card=math&code=%5Ctheta%3D%5Ctheta%5E%7B%28t%29%7D)时对应等号成立的情况，即S06P02-EM算法 - 图35%7D%2C%5Ctheta%5E%7B(t)%7D)%3DL(%5Ctheta%5E%7B(t)%7D)#card=math&code=B%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%3DL%28%5Ctheta%5E%7B%28t%29%7D%29)；而在S06P02-EM算法 - 图36%7D#card=math&code=%5Ctheta%5Cne%5Ctheta%5E%7B%28t%29%7D)时，等号不成立，但是仍然满足S06P02-EM算法 - 图37%7D)%5Clt%20L(%5Ctheta)#card=math&code=B%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clt%20L%28%5Ctheta%29)。最大化S06P02-EM算法 - 图38#card=math&code=L%28%5Ctheta%29)就是在每一轮迭代都对S06P02-EM算法 - 图39%7D)#card=math&code=B%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29)求最大，然后迭代至收敛即可

S06P02-EM算法 - 图40%7D%26%3D%5Carg%5Cmax%7B%5Ctheta%7D%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ-%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)dZ%5C%5C%0A%26%3D%5Carg%5Cmax%7B%5Ctheta%7D%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ%5C%5C%0A%26%3D%5Carg%5Cmax%7B%5Ctheta%7DQ(%5Ctheta%2C%5Ctheta%5E%7B(t)%7D)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Ctheta%5E%7B%28t%2B1%29%7D%26%3D%5Carg%5Cmax%7B%5Ctheta%7D%5Csum%7Bi%3D1%7D%5EN%5CintZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ-%5Csum%7Bi%3D1%7D%5EN%5CintZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29dZ%5C%5C%0A%26%3D%5Carg%5Cmax%7B%5Ctheta%7D%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ%5C%5C%0A%26%3D%5Carg%5Cmax%7B%5Ctheta%7DQ%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%0A%5Cend%7Baligned%7D%0A)

于是最终转化为每一轮最大化S06P02-EM算法 - 图41%7D)%3D%5Csum%7Bi%3D1%7D%5ENQ_i(%5Ctheta%2C%5Ctheta%5E%7B(t)%7D)#card=math&code=Q%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%3D%5Csum%7Bi%3D1%7D%5ENQ_i%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29)

S06P02-EM算法 - 图42%7D)%3D%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ%3DE%7BP(Z%7CXi%2C%5Ctheta%5E%7B(t)%7D)%7D%5B%5Clog%20P(X_i%2CZ%7C%5Ctheta)%5D%0A#card=math&code=Q_i%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%3D%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ%3DE%7BP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%7D%5B%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29%5D%0A)

这就是EM算法的来源，E代表求期望S06P02-EM算法 - 图43%7D)%7D%5B%5Clog%20P(Xi%2CZ%7C%5Ctheta)%5D#card=math&code=E%7BP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%7D%5B%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29%5D)，M代表最大化这个期望

ELBO和Jensen不等式

还可以从另外一个角度来理解，还是从对数似然函数角度出发

S06P02-EM算法 - 图44%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P(X_i%7C%5Ctheta)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5CintZP(X_i%2CZ%7C%5Ctheta)dZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5CintZ%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DP_i(Z)dZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20E%7BP_i(Z)%7D%5Cleft%5B%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20P%28Xi%7C%5Ctheta%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5CintZP%28X_i%2CZ%7C%5Ctheta%29dZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5CintZ%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DP_i%28Z%29dZ%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%20E_%7BP_i%28Z%29%7D%5Cleft%5B%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D%5Cright%5D%0A%5Cend%7Baligned%7D%0A)

其中S06P02-EM算法 - 图45#card=math&code=P_i%28Z%29)为关于S06P02-EM算法 - 图46的一个概率分布，满足S06P02-EM算法 - 图47dZ%3D1#card=math&code=%5Cint_ZP_i%28Z%29dZ%3D1)。根据Jensen不等式有

S06P02-EM算法 - 图48%7D%5Cleft%5B%5Cfrac%7BP(Xi%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7D%5Cright%5D%26%5Cge%20E%7BPi(Z)%7D%5Cleft%5B%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7D%5Cright%5D%5C%5C%0A%26%3D%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ%5C%5C%0A%26%3DELBO_i%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Clog%20E%7BPi%28Z%29%7D%5Cleft%5B%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D%5Cright%5D%26%5Cge%20E%7BP_i%28Z%29%7D%5Cleft%5B%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D%5Cright%5D%5C%5C%0A%26%3D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%5C%5C%0A%26%3DELBO_i%0A%5Cend%7Baligned%7D%0A)

等号在S06P02-EM算法 - 图49%7D%7BP_i(Z)%7D#card=math&code=%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D)为常数时成立

S06P02-EM算法 - 图50%7D%7BP_i(Z)%7D%3DC%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%20P_i(Z)%3D%7B1%5Cover%20C%7DP(X_i%2CZ%7C%5Ctheta)%5C%5C%0A%26%5CRightarrow%5Cint_ZP_i(Z)dZ%3D%5Cint_Z%7B1%5Cover%20C%7DP(X_i%2CZ%7C%5Ctheta)dZ%5C%5C%0A%26%5CRightarrow%20C%3DP(X_i%7C%5Ctheta)%5C%5C%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7D%3DC%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%20P_i%28Z%29%3D%7B1%5Cover%20C%7DP%28X_i%2CZ%7C%5Ctheta%29%5C%5C%0A%26%5CRightarrow%5Cint_ZP_i%28Z%29dZ%3D%5Cint_Z%7B1%5Cover%20C%7DP%28X_i%2CZ%7C%5Ctheta%29dZ%5C%5C%0A%26%5CRightarrow%20C%3DP%28X_i%7C%5Ctheta%29%5C%5C%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A)

将S06P02-EM算法 - 图51#card=math&code=C%3DP%28X_i%7C%5Ctheta%29)代入即得

S06P02-EM算法 - 图52%3D%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP(X_i%7C%5Ctheta)%7D%3DP(Z%7CX_i%2C%5Ctheta)%0A#card=math&code=P_i%28Z%29%3D%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP%28X_i%7C%5Ctheta%29%7D%3DP%28Z%7CX_i%2C%5Ctheta%29%0A)

这和用KL散度方法得到的结果一致，也是在每一轮用后验概率S06P02-EM算法 - 图53#card=math&code=P%28Z%7CX_i%2C%5Ctheta%29)来估计S06P02-EM算法 - 图54#card=math&code=P_i%28Z%29)，后续推导也与前一种方法等价

EM算法

一般地，用S06P02-EM算法 - 图55表示观测到的样本，用S06P02-EM算法 - 图56表示隐变量，模型参数为S06P02-EM算法 - 图57，S06P02-EM算法 - 图58和S06P02-EM算法 - 图59联合数据称为完全数据，S06P02-EM算法 - 图60可称为不完全数据。在给定观测数据S06P02-EM算法 - 图61时，不完全数据的对数似然函数为S06P02-EM算法 - 图62#card=math&code=%5Clog%20P%28X%7C%5Ctheta%29)，S06P02-EM算法 - 图63和S06P02-EM算法 - 图64的联合概率分布为S06P02-EM算法 - 图65#card=math&code=P%28X%2CZ%7C%5Ctheta%29)，完全数据的对数似然函数为S06P02-EM算法 - 图66#card=math&code=%5Clog%20P%28X%2CZ%7C%5Ctheta%29)
EM算法通过迭代求解S06P02-EM算法 - 图67#card=math&code=%5Clog%20P%28X%7C%5Ctheta%29)的极大似然估计，每次迭代都包含两步：E步，求期望(Expectation)；M步，求极大化(Maximization)。下面先给出EM算法的具体流程

  • 算法流程：

    (1)选择参数初值S06P02-EM算法 - 图68%7D#card=math&code=%5Ctheta%5E%7B%280%29%7D)
    (2)E步：记S06P02-EM算法 - 图69%7D#card=math&code=%5Ctheta%5E%7B%28i%29%7D)为第S06P02-EM算法 - 图70次迭代参数的估计值，在第S06P02-EM算法 - 图71次迭代计算下式

S06P02-EM算法 - 图72%7D)%26%3DE%7BZ%7CX%2C%5Ctheta%5E%7B(i)%7D%7D%5B%5Clog%20P(X%2CZ%7C%5Ctheta)%5D%5C%5C%0A%26%3D%5Cint_Z%5Clog%20P(X%2CZ%7C%5Ctheta)P(Z%7CX%2C%5Ctheta%5E%7B(i)%7D)dZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AQ%28%5Ctheta%2C%5Ctheta%5E%7B%28i%29%7D%29%26%3DE%7BZ%7CX%2C%5Ctheta%5E%7B%28i%29%7D%7D%5B%5Clog%20P%28X%2CZ%7C%5Ctheta%29%5D%5C%5C%0A%26%3D%5Cint_Z%5Clog%20P%28X%2CZ%7C%5Ctheta%29P%28Z%7CX%2C%5Ctheta%5E%7B%28i%29%7D%29dZ%0A%5Cend%7Baligned%7D%0A)

S06P02-EM算法 - 图73%7D)#card=math&code=P%28Z%7CX%2C%5Ctheta%5E%7B%28i%29%7D%29)是给定观测数据S06P02-EM算法 - 图74和当前参数估计S06P02-EM算法 - 图75%7D#card=math&code=%5Ctheta%5E%7B%28i%29%7D)下隐变量S06P02-EM算法 - 图76的条件分布
(3)M步：求使S06P02-EM算法 - 图77%7D)#card=math&code=Q%28%5Ctheta%2C%5Ctheta%5E%7B%28i%29%7D%29)极大化的S06P02-EM算法 - 图78，即第S06P02-EM算法 - 图79次迭代的参数估计值S06P02-EM算法 - 图80%7D#card=math&code=%5Ctheta%5E%7B%28i%2B1%29%7D)

S06P02-EM算法 - 图81%7D%3D%5Carg%5Cmax%5Ctheta%20Q(%5Ctheta%2C%5Ctheta%5E%7B(i)%7D)%0A#card=math&code=%5Ctheta%5E%7B%28i%2B1%29%7D%3D%5Carg%5Cmax%5Ctheta%20Q%28%5Ctheta%2C%5Ctheta%5E%7B%28i%29%7D%29%0A)

(4)重复步骤(2)、(3)，直到达到收敛条件

EM算法理解

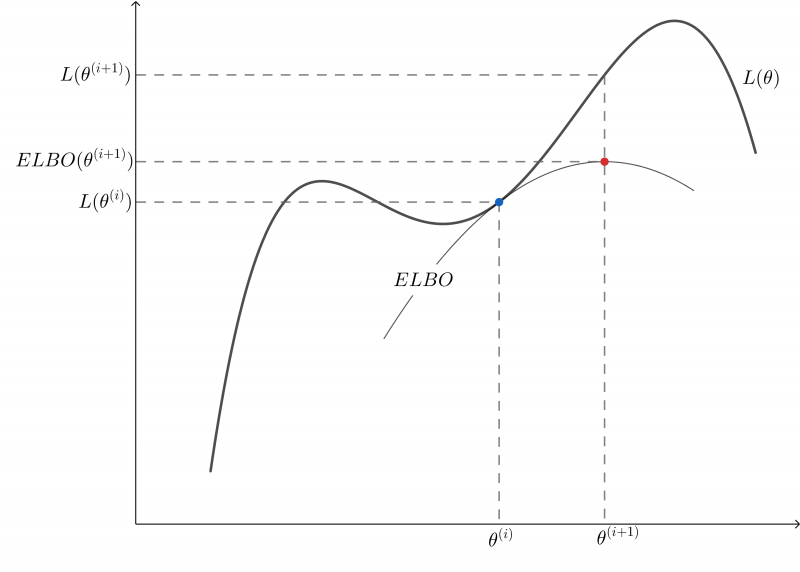
通过推导我们可以看出，在每一轮迭代实际都是在最大化S06P02-EM算法 - 图82%3D%5Clog%20P(X%7C%5Ctheta)#card=math&code=L%28%5Ctheta%29%3D%5Clog%20P%28X%7C%5Ctheta%29)的一个下界，通过不断的最大化这个下界，最终使S06P02-EM算法 - 图83#card=math&code=L%28%5Ctheta%29)本身达到最大，如下图的过程

S06P02-EM算法 - 图84

EM算法的收敛性

EM的收敛性包含两层：关于对数似然函数序列S06P02-EM算法 - 图85%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29)的收敛性和参数序列S06P02-EM算法 - 图86%7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D)的收敛性。而且算法的收敛性只能保证参数序列一定能收敛于对数似然函数序列的稳定点，不保证收敛到对数似然函数序列的极大值点，因此初始值的设定很重要。对于凸优化问题肯定能收敛至最优解，对于非凸优化问题，可能收敛至局部最优点

  • 下面只证明对数似然函数序列的S06P02-EM算法 - 图87%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29)收敛性：
    如果对数似然函数有极大值，要证明对数似然函数序列的S06P02-EM算法 - 图88%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29)收敛，即要证明S06P02-EM算法 - 图89%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29)是单调递增的，即证S06P02-EM算法 - 图90%7D)%5Cle%20L(%5Ctheta%5E%7B(t%2B1)%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29%5Cle%20L%28%5Ctheta%5E%7B%28t%2B1%29%7D%29)
    根据EM算法的推导可得S06P02-EM算法 - 图91%3D%5Csum%7Bi%3D1%7D%5ENleft_i%3D%5Csum%7Bi%3D1%7D%5ENQi(%5Ctheta%2C%5Ctheta%5E%7B(t)%7D)-%5Csum%7Bi%3D1%7D%5EN%5CintZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta)dZ%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AL%28%5Ctheta%29%3D%5Csum%7Bi%3D1%7D%5ENlefti%3D%5Csum%7Bi%3D1%7D%5ENQi%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29-%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%29dZ%0A%5Cend%7Bgathered%7D%0A)
    S06P02-EM算法 - 图92%7D)%3D%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta)dZ%0A#card=math&code=H_i%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29%3D%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%29dZ%0A)

将变量S06P02-EM算法 - 图93分别取S06P02-EM算法 - 图94%7D%2C%5Ctheta%5E%7B(t%2B1)%7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%2B1%29%7D)，考虑下式S06P02-EM算法 - 图95%7D%2C%5Ctheta%5E%7B(t)%7D)-H_i(%5Ctheta%5E%7B(t)%7D%2C%5Ctheta%5E%7B(t)%7D)%5C%5C%0A%3D%26%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta%5E%7B(t%2B1)%7D)dZ-%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%20P(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)dZ%5C%5C%0A%3D%26%5Cint_ZP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%5Clog%5Cfrac%7BP(Z%7CX_i%2C%5Ctheta%5E%7B(t%2B1)%7D)%7D%7BP(Z%7CX_i%2C%5Ctheta%5E%7B(t)%7D)%7DdZ%5C%5C%0A%3D%26-KL%5Cleft%5BZ%7CX_i%2C%5Ctheta%5E%7B(t)%7D%7C%7CZ%7CX_i%2C%5Ctheta%5E%7B(t%2B1)%7D)%5Cright%5D%5C%5C%0A%5Cle%260%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26H_i%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29-H_i%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5C%5C%0A%3D%26%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%2B1%29%7D%29dZ-%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%20P%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29dZ%5C%5C%0A%3D%26%5Cint_ZP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%5Clog%5Cfrac%7BP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%2B1%29%7D%29%7D%7BP%28Z%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%29%7DdZ%5C%5C%0A%3D%26-KL%5Cleft%5BZ%7CX_i%2C%5Ctheta%5E%7B%28t%29%7D%7C%7CZ%7CX_i%2C%5Ctheta%5E%7B%28t%2B1%29%7D%29%5Cright%5D%5C%5C%0A%5Cle%260%0A%5Cend%7Baligned%7D%0A)

因为每次迭代要对S06P02-EM算法 - 图96%7D)#card=math&code=Qi%28%5Ctheta%2C%5Ctheta%5E%7B%28t%29%7D%29)极大化，所以显然S06P02-EM算法 - 图97%7D%2C%5Ctheta%5E%7B(t)%7D)%5Cle%20Q_i(%5Ctheta%5E%7B(t%2B1)%7D%2C%5Ctheta%5E%7B(t)%7D)#card=math&code=Q_i%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5Cle%20Q_i%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29)S06P02-EM算法 - 图98%7D)-L(%5Ctheta%5E%7B(t)%7D)%26%3D%5Cleft%5B%5Csum%7Bi%3D1%7D%5ENQi(%5Ctheta%5E%7B(t%2B1)%7D%2C%5Ctheta%5E%7B(t)%7D)-%5Csum%7Bi%3D1%7D%5ENHi(%5Ctheta%5E%7B(t%2B1)%7D%2C%5Ctheta%5E%7B(t)%7D)%5Cright%5D-%5Cleft%5B%5Csum%7Bi%3D1%7D%5ENQi(%5Ctheta%5E%7B(t)%7D%2C%5Ctheta%5E%7B(t)%7D)-%5Csum%7Bi%3D1%7D%5ENHi(%5Ctheta%5E%7B(t)%7D%2C%5Ctheta%5E%7B(t)%7D)%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5BQi(%5Ctheta%5E%7B(t%2B1)%7D%2C%5Ctheta%5E%7B(t)%7D)-Q_i(%5Ctheta%5E%7B(t)%7D%2C%5Ctheta%5E%7B(t)%7D)%5Cright%5D-%5Csum%7Bi%3D1%7D%5EN%5Cleft%5BHi(%5Ctheta%5E%7B(t%2B1)%7D%2C%5Ctheta%5E%7B(t)%7D)-H_i(%5Ctheta%5E%7B(t)%7D%2C%5Ctheta%5E%7B(t)%7D)%5Cright%5D%5C%5C%0A%26%5Cge0%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%5E%7B%28t%2B1%29%7D%29-L%28%5Ctheta%5E%7B%28t%29%7D%29%26%3D%5Cleft%5B%5Csum%7Bi%3D1%7D%5ENQi%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29-%5Csum%7Bi%3D1%7D%5ENHi%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5Cright%5D-%5Cleft%5B%5Csum%7Bi%3D1%7D%5ENQi%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29-%5Csum%7Bi%3D1%7D%5ENHi%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5BQi%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29-Q_i%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5Cright%5D-%5Csum%7Bi%3D1%7D%5EN%5Cleft%5BH_i%28%5Ctheta%5E%7B%28t%2B1%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29-H_i%28%5Ctheta%5E%7B%28t%29%7D%2C%5Ctheta%5E%7B%28t%29%7D%29%5Cright%5D%5C%5C%0A%26%5Cge0%0A%5Cend%7Baligned%7D%0A)

因此对数似然函数序列S06P02-EM算法 - 图99%7D)#card=math&code=L%28%5Ctheta%5E%7B%28t%29%7D%29)是单调递增的，只要S06P02-EM算法 - 图100#card=math&code=L%28%5Ctheta%29)有极大值则EM算法一定可以收敛

广义EM算法

上面介绍的EM算法中，在E步计算期望时，我们令S06P02-EM算法 - 图101%3DP_i(Z%7CX_i%2C%5Ctheta)#card=math&code=P_i%28Z%29%3DP_i%28Z%7CX_i%2C%5Ctheta%29)，但是在实际情况中，S06P02-EM算法 - 图102#card=math&code=P_i%28Z%7CX_i%2C%5Ctheta%29)也有可能计算不出来，这样等号就不能成立，这种情况下就要考虑新的方法来极大化S06P02-EM算法 - 图103#card=math&code=L%28%5Ctheta%29)。根据之前的推导

S06P02-EM算法 - 图104%26%3DELBO%2BKL%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5ENELBO_i%2B%5Csum%7Bi%3D1%7D%5ENKL(Pi(Z)%7C%7CP(Z%7CX_i%2C%5Ctheta))%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ-%5Csum%7Bi%3D1%7D%5EN%5CintZP_i(Z)%5Clog%5Cfrac%7BP(Z%7CX_i%2C%5Ctheta)%7D%7BP_i(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%26%3DELBO%2BKL%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5ENELBOi%2B%5Csum%7Bi%3D1%7D%5ENKL%28Pi%28Z%29%7C%7CP%28Z%7CX_i%2C%5Ctheta%29%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CintZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ-%5Csum%7Bi%3D1%7D%5EN%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28Z%7CX_i%2C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A)

根据上式，如果固定S06P02-EM算法 - 图105，那么S06P02-EM算法 - 图106#card=math&code=L%28%5Ctheta%29)不变，按照之前的想法要让S06P02-EM算法 - 图107，但是在S06P02-EM算法 - 图108#card=math&code=P_i%28Z%7CX_i%2C%5Ctheta%29)计算不出来时只能作为一个优化问题来求解，也就是最小化S06P02-EM算法 - 图109的问题，等价于最大化S06P02-EM算法 - 图110，此时对应的S06P02-EM算法 - 图111%3D%5Chat%7BP_i%7D(Z)#card=math&code=P_i%28Z%29%3D%5Chat%7BP_i%7D%28Z%29)；在S06P02-EM算法 - 图112#card=math&code=%5Chat%7BP_i%7D%28Z%29)下，对S06P02-EM算法 - 图113极大化S06P02-EM算法 - 图114#card=math&code=L%28%5Ctheta%29)，如此迭代就可以达到极大化S06P02-EM算法 - 图115#card=math&code=L%28%5Ctheta%29)的目的。这就是广义EM算法的基本思想

Generalized EM

广义EM算法(GEM)流程

(1)选择参数初值S06P02-EM算法 - 图116%7D#card=math&code=%5Ctheta%5E%7B%280%29%7D)
(2)E步：记S06P02-EM算法 - 图117%7D(Z)#card=math&code=P_i%5E%7B%28t%29%7D%28Z%29)为第S06P02-EM算法 - 图118次迭代S06P02-EM算法 - 图119#card=math&code=P_i%28Z%29)的估计值，S06P02-EM算法 - 图120%7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D)为第S06P02-EM算法 - 图121次迭代参数的估计值，在第S06P02-EM算法 - 图122次迭代计算固定S06P02-EM算法 - 图123%7D#card=math&code=%5Ctheta%3D%5Ctheta%5E%7B%28t%29%7D)时的优化问题

S06P02-EM算法 - 图124%7D(Z)%26%3D%5Carg%5Cmax%7BP_i(Z)%7DELBO_i%5C%5C%0A%26%3D%5Carg%5Cmax%7BPi(Z)%7DE%7BPi(Z)%7D%5Cleft%5B%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta%5E%7B(t)%7D)%7D%7BP_i(Z)%7D%5Cright%5D%5C%5C%0A%26%3D%5Carg%5Cmax%7BPi(Z)%7D%5Cint_ZP_i(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta%5E%7B(t)%7D)%7D%7BP_i(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP_i%5E%7B%28t%2B1%29%7D%28Z%29%26%3D%5Carg%5Cmax%7BPi%28Z%29%7DELBO_i%5C%5C%0A%26%3D%5Carg%5Cmax%7BPi%28Z%29%7DE%7BPi%28Z%29%7D%5Cleft%5B%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%5E%7B%28t%29%7D%29%7D%7BP_i%28Z%29%7D%5Cright%5D%5C%5C%0A%26%3D%5Carg%5Cmax%7BP_i%28Z%29%7D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%5E%7B%28t%29%7D%29%7D%7BP_i%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A)

(3)M步：极大化在S06P02-EM算法 - 图125%3DP_i%5E%7B(t%2B1)%7D(Z)#card=math&code=P_i%28Z%29%3DP_i%5E%7B%28t%2B1%29%7D%28Z%29)时的S06P02-EM算法 - 图126，即求第S06P02-EM算法 - 图127次迭代的参数估计值S06P02-EM算法 - 图128%7D#card=math&code=%5Ctheta%5E%7B%28t%2B1%29%7D)

S06P02-EM算法 - 图129%7D%26%3D%5Carg%5Cmax%5Ctheta%20ELBO_i%5C%5C%0A%26%3D%5Carg%5Cmax%5Ctheta%5CintZP_i%5E%7B(t%2B1)%7D(Z)%5Clog%5Cfrac%7BP(X_i%2CZ%7C%5Ctheta)%7D%7BP_i%5E%7B(t%2B1)%7D(Z)%7DdZ%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Ctheta%5E%7B%28t%2B1%29%7D%26%3D%5Carg%5Cmax%5Ctheta%20ELBOi%5C%5C%0A%26%3D%5Carg%5Cmax%5Ctheta%5Cint_ZP_i%5E%7B%28t%2B1%29%7D%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%5E%7B%28t%2B1%29%7D%28Z%29%7DdZ%0A%5Cend%7Baligned%7D%0A)

(4)重复步骤(2)、(3)，直到达到收敛条件

可以看到实际上GEM就是一种坐标上升法
我们研究一下此时的S06P02-EM算法 - 图130

S06P02-EM算法 - 图131%5Clog%5Cfrac%7BP(Xi%2CZ%7C%5Ctheta)%7D%7BP_i(Z)%7DdZ%5C%5C%0A%26%3D%5Cint_ZP_i(Z)%5Clog%20P(X_i%2CZ%7C%5Ctheta)dZ-%5Cint_ZP_i(Z)%5Clog%20P_i(Z)dZ%5C%5C%0A%26%3DE%7BPi(Z)%7D%5B%5Clog%20P(X_i%2CZ%7C%5Ctheta)%5D%2BH%5BP_i(Z)%5D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AELBO_i%26%3D%5Cint_ZP_i%28Z%29%5Clog%5Cfrac%7BP%28X_i%2CZ%7C%5Ctheta%29%7D%7BP_i%28Z%29%7DdZ%5C%5C%0A%26%3D%5Cint_ZP_i%28Z%29%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29dZ-%5Cint_ZP_i%28Z%29%5Clog%20P_i%28Z%29dZ%5C%5C%0A%26%3DE%7BP_i%28Z%29%7D%5B%5Clog%20P%28X_i%2CZ%7C%5Ctheta%29%5D%2BH%5BP_i%28Z%29%5D%0A%5Cend%7Baligned%7D%0A)

其中S06P02-EM算法 - 图132%5D%3D-%5Cint_ZP_i(Z)%5Clog%20P_i(Z)dZ#card=math&code=H%5BP_i%28Z%29%5D%3D-%5Cint_ZP_i%28Z%29%5Clog%20P_i%28Z%29dZ)为S06P02-EM算法 - 图133#card=math&code=P_i%28Z%29)的熵
一般地，令F函数

S06P02-EM算法 - 图134%2C%5Ctheta)%3DELBO_i%0A#card=math&code=F%28P_i%28Z%29%2C%5Ctheta%29%3DELBO_i%0A)

此时的GEM算法又称为F-MM算法

GEM的变种

实际在GEM算法中，在E-Step和M-Step分别求解优化问题时，可能都很难求解，因此针对这两步优化运用不同的方法，又可以衍生出更广泛的EM算法，主要有以下两种

  1. VEM/VBEM：在求解E-Step和M-Step分别求解优化问题时运用变分推断(VI)的方法
  2. MCEM：在求解E-Step和M-Step分别求解优化问题时运用马尔可夫链蒙特卡罗方法(MCMC)