最小二乘法

给定数据集S02-线性回归 - 图1%2C(X_2%2Cy_2)%2C%5Ccdots%2C(X_N%2Cy_N)%5C%7D#card=math&code=D%3D%5C%7B%28X_1%2Cy_1%29%2C%28X_2%2Cy_2%29%2C%5Ccdots%2C%28X_N%2Cy_N%29%5C%7D&height=20&width=281)，其中S02-线性回归 - 图2

S02-线性回归 - 图3%5ET%3D%0A%5Cbegin%7Bpmatrix%7D%0A1%26x%7B11%7D%26x%7B12%7D%26%5Ccdots%26x%7B1p%7D%5C%5C%0A1%26x%7B21%7D%26x%7B22%7D%26%5Ccdots%26x%7B2p%7D%5C%5C%0A%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%26%5Cvdots%5C%5C%0A1%26x%7BN1%7D%26x%7BN2%7D%26%5Ccdots%26x%7BNp%7D%0A%5Cend%7Bpmatrix%7D%7BN%5Ctimes(p%2B1)%7D%5C%5C%0AY%26%3D%5Cbegin%7Bpmatrix%7Dy1%5C%5Cy_2%5C%5C%5Cvdots%5C%5Cy_N%5Cend%7Bpmatrix%7D%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AX%26%3D%28X_1%2CX_2%2C%5Ccdots%2CX_N%29%5ET%3D%0A%5Cbegin%7Bpmatrix%7D%0A1%26x%7B11%7D%26x%7B12%7D%26%5Ccdots%26x%7B1p%7D%5C%5C%0A1%26x%7B21%7D%26x%7B22%7D%26%5Ccdots%26x%7B2p%7D%5C%5C%0A%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%26%5Cvdots%5C%5C%0A1%26x%7BN1%7D%26x%7BN2%7D%26%5Ccdots%26x%7BNp%7D%0A%5Cend%7Bpmatrix%7D_%7BN%5Ctimes%28p%2B1%29%7D%5C%5C%0AY%26%3D%5Cbegin%7Bpmatrix%7Dy_1%5C%5Cy_2%5C%5C%5Cvdots%5C%5Cy_N%5Cend%7Bpmatrix%7D%5C%5C%0A%5Cend%7Baligned%7D%0A&height=212&width=468)

最小二乘法就是要拟合函数S02-线性回归 - 图4%3DW_x%5ETX%5E%7B’%7D%2Bb%3DW_x%5ETX%5E%7B’%7D%2Bw_0%5Ccdot%201%3DW%5ETX#card=math&code=f%28W%29%3DW_x%5ETX%5E%7B%27%7D%2Bb%3DW_x%5ETX%5E%7B%27%7D%2Bw_0%5Ccdot%201%3DW%5ETX&height=24&width=334)，其中S02-线性回归 - 图5%5ET#card=math&code=W%3D%28w_0%2Cw_1%2Cw_2%2C%5Ccdots%2Cw_p%29%5ET&height=24&width=194)

最小二乘估计(Least Square Estimate,LSE)

损失函数为

S02-线性回归 - 图6%26%3D%5Csum%7Bi%3D1%7D%5EN%7B%7C%7CW%5ETX_i-y_i%7C%7C%7D%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN(W%5ETXi-y_i)%5E2%5C%5C%0A%26%3D%5Cbegin%7Bpmatrix%7DW%5ETX_1-y_1%26W%5ETX_2-y_2%26%5Ccdots%26W%5ETX_N-y_N%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DW%5ETX_1-y_1%5C%5CW%5ETX_2-y_2%5C%5C%5Cvdots%5C%5CW%5ETX_N-y_N%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D(W%5ETX%5ET-Y%5ET)(XW-Y)%5C%5C%0A%26%3DW%5ETX%5ETXW-W%5ETX%5ETY-Y%5ETXW%2BY%5ETY%5C%5C%0A%26%3DW%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%5C%5C%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Chat%7BW%7D%3D%5Carg%5Cmin_WL(W)%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20L(W)%7D%7B%5Cpartial%20W%7D%3D2X%5ETXW-2X%5ETY%3D0%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Chat%7BW%7D%3D(X%5ETX)%5E%7B-1%7DX%5ETY%3DX%5E%7B%5Cdagger%7DY%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Cbegin%7Baligned%7D%0AL%28W%29%26%3D%5Csum%7Bi%3D1%7D%5EN%7B%7C%7CW%5ETXi-y_i%7C%7C%7D%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%5C%5C%0A%26%3D%5Cbegin%7Bpmatrix%7DW%5ETX_1-y_1%26W%5ETX_2-y_2%26%5Ccdots%26W%5ETX_N-y_N%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DW%5ETX_1-y_1%5C%5CW%5ETX_2-y_2%5C%5C%5Cvdots%5C%5CW%5ETX_N-y_N%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%28W%5ETX%5ET-Y%5ET%29%28XW-Y%29%5C%5C%0A%26%3DW%5ETX%5ETXW-W%5ETX%5ETY-Y%5ETXW%2BY%5ETY%5C%5C%0A%26%3DW%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%5C%5C%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Chat%7BW%7D%3D%5Carg%5Cmin_WL%28W%29%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20L%28W%29%7D%7B%5Cpartial%20W%7D%3D2X%5ETXW-2X%5ETY%3D0%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Chat%7BW%7D%3D%28X%5ETX%29%5E%7B-1%7DX%5ETY%3DX%5E%7B%5Cdagger%7DY%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A&height=450&width=565)

几何解释

设S02-线性回归 - 图7#card=math&code=X%3D%28X_0%2CX_1%2C%5Ccdots%2CX_p%29&height=21&width=159)，其中S02-线性回归 - 图8为列向量，那么S02-线性回归 - 图9%3DXW#card=math&code=f%28W%29%3DXW&height=20&width=94)，即S02-线性回归 - 图10#card=math&code=f%28W%29&height=20&width=40)为S02-线性回归 - 图11张成的p维空间中的向量，S02-线性回归 - 图12#card=math&code=f%28W%29&height=20&width=40)为S02-线性回归 - 图13列向量的线性组合

S02-线性回归 - 图14%3Dw_0X_0%2Bw_1X_1%2B%5Ccdots%2Bw_pX_p%0A#card=math&code=f%28W%29%3Dw_0X_0%2Bw_1X_1%2B%5Ccdots%2Bw_pX_p%0A&height=21&width=267)

S02-线性回归 - 图15为S02-线性回归 - 图16所张成的空间外的一个向量，若要用一个合适的S02-线性回归 - 图17#card=math&code=f%28W%29&height=20&width=40)拟合S02-线性回归 - 图18，那么只需要找到S02-线性回归 - 图19所张成的空间中距离S02-线性回归 - 图20最近的向量，显然为S02-线性回归 - 图21在S02-线性回归 - 图22张成的空间中的投影，则有

S02-线性回归 - 图23)%3D0%5C%5C%0A%26%5CRightarrow%20X%5ET(Y-XW)%3D0%5C%5C%0A%26%5CRightarrow%20%5Chat%7BW%7D%3D(X%5ETX)%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26X%5ET%28Y-f%28W%29%29%3D0%5C%5C%0A%26%5CRightarrow%20X%5ET%28Y-XW%29%3D0%5C%5C%0A%26%5CRightarrow%20%5Chat%7BW%7D%3D%28X%5ETX%29%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A&height=74&width=177)

概率角度解释

设S02-线性回归 - 图24#card=math&code=%5Cepsilon%5Csim%20N%280%2C%5Csigma%5E2%29&height=23&width=90)，则有S02-线性回归 - 图25%2B%5Cepsilon%3DW%5ETX%2B%5Cepsilon#card=math&code=Y%3Df%28W%29%2B%5Cepsilon%3DW%5ETX%2B%5Cepsilon&height=23&width=194)，显然

S02-线性回归 - 图26%26%5Csim%20N(W%5ETXi%2C%5Csigma%5E2)%5C%5C%0AP(y_i%7CX_i%3BW)%26%3D%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D(y_i-W%5ETX_i)%5E2)%5C%5C%0AP(Y%7CX%3BW)%26%3D%5Cprod%7Bi%3D1%7D%5ENP(yi%7CX_i%3BW)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%28y_i%7CX_i%3BW%29%26%5Csim%20N%28W%5ETX_i%2C%5Csigma%5E2%29%5C%5C%0AP%28y_i%7CX_i%3BW%29%26%3D%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%28y_i-W%5ETX_i%29%5E2%29%5C%5C%0AP%28Y%7CX%3BW%29%26%3D%5Cprod%7Bi%3D1%7D%5ENP%28y_i%7CX_i%3BW%29%0A%5Cend%7Baligned%7D%0A&height=122&width=362)

根据极大似然估计有

S02-线性回归 - 图27%26%3D%5Clog%7BP(Y%7CX%3BW)%7D%5C%5C%0A%26%3D%5Clog%5Cprod%7Bi%3D1%7D%5ENP(y_i%7CX_i%3BW)%5C%5C%0A%26%3D%5Clog%5Cprod%7Bi%3D1%7D%5EN%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D(yi-W%5ETX_i)%5E2%5Cright)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft(%5Clog%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D(yi-W%5ETX_i)%5E2%5Cright)%5C%5C%0A%5C%5C%0A%5Chat%7BW%7D%26%3D%5Carg%5Cmax_WL(W)%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Cleft(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D(yi-W%5ETX_i)%5E2%5Cright)%5C%5C%0A%26%3D%5Carg%5Cmin_W%5Csum%7Bi%3D1%7D%5EN(yi-W%5ETX_i)%5E2%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28W%29%26%3D%5Clog%7BP%28Y%7CX%3BW%29%7D%5C%5C%0A%26%3D%5Clog%5Cprod%7Bi%3D1%7D%5ENP%28yi%7CX_i%3BW%29%5C%5C%0A%26%3D%5Clog%5Cprod%7Bi%3D1%7D%5EN%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%28yi-W%5ETX_i%29%5E2%5Cright%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%28%5Clog%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%28yi-W%5ETX_i%29%5E2%5Cright%29%5C%5C%0A%5C%5C%0A%5Chat%7BW%7D%26%3D%5Carg%5Cmax_WL%28W%29%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Cleft%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%28yi-W%5ETX_i%29%5E2%5Cright%29%5C%5C%0A%26%3D%5Carg%5Cmin_W%5Csum%7Bi%3D1%7D%5EN%28y_i-W%5ETX_i%29%5E2%0A%5Cend%7Baligned%7D%0A&height=349&width=375)

故最小二乘估计等价于噪声为高斯分布的极大似然估计

线性回归的正则化

S02-线性回归 - 图28%26%3D%5Csum%7Bi%3D1%7D%5EN(W%5ETX_i-y_i)%5E2%5C%5C%0A%5Chat%7BW%7D%26%3D(X%5ETX)%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28W%29%26%3D%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%5C%5C%0A%5Chat%7BW%7D%26%3D%28X%5ETX%29%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A&height=78&width=197)

过拟合

  • 实际数据集观测数少或维数过多，此时造成S02-线性回归 - 图29不可逆，那么S02-线性回归 - 图30没有解析解。具体表现为模型过拟合
  • 解决方法：
    1. 增加数据量
    2. 特征选择/特征提取（降维）
    3. 正则化

正则化

S02-线性回归 - 图31%2B%5Clambda%20P(W)%5D%0A#card=math&code=%5Carg%5Cmin_W%5BL%28W%29%2B%5Clambda%20P%28W%29%5D%0A&height=28&width=179)

其中S02-线性回归 - 图32#card=math&code=L%28W%29&height=20&width=41)称为损失函数(Loss Function)，S02-线性回归 - 图33#card=math&code=P%28W%29&height=20&width=43)称为惩罚项(Penalty)

  • 正则化一般有两种
    1. L1正则化，又叫Lasso：S02-线性回归 - 图34%3D%7C%7CW%7C%7C_1#card=math&code=P%28W%29%3D%7C%7CW%7C%7C_1&height=20&width=109)
    2. L2正则化，又叫岭回归(Ridge Regression)：S02-线性回归 - 图35%3D%7C%7CW%7C%7C_2%5E2%3DW%5ETW#card=math&code=P%28W%29%3D%7C%7CW%7C%7C_2%5E2%3DW%5ETW&height=24&width=177)

L2正则化

岭回归推导

令S02-线性回归 - 图36%3DL(W)%2B%5Clambda%20P(W)#card=math&code=J%28W%29%3DL%28W%29%2B%5Clambda%20P%28W%29&height=20&width=179)，则

S02-线性回归 - 图37%26%3D%5Csum%7Bi%3D1%7D%5EN(W%5ETX_i-y_i)%5E2%2B%5Clambda%20W%5ETW%5C%5C%0A%26%3DW%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%2B%5Clambda%20W%5ETW%5C%5C%0A%26%3DW%5ET(X%5ETX%2B%5Clambda%20I)W-2W%5ETX%5ETY%2BY%5ETY%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20J(W)%7D%7B%5Cpartial%20W%7D%3D2(X%5ETX%2B%5Clambda%20I)W-2X%5ETY%3D0%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Chat%7BW%7D%3D(X%5ETX%2B%5Clambda%20I)%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Cbegin%7Baligned%7D%0AJ%28W%29%26%3D%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%2B%5Clambda%20W%5ETW%5C%5C%0A%26%3DW%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%2B%5Clambda%20W%5ETW%5C%5C%0A%26%3DW%5ET%28X%5ETX%2B%5Clambda%20I%29W-2W%5ETX%5ETY%2BY%5ETY%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20J%28W%29%7D%7B%5Cpartial%20W%7D%3D2%28X%5ETX%2B%5Clambda%20I%29W-2X%5ETY%3D0%5C%5C%0A%5C%5C%0A%26%5CRightarrow%5Chat%7BW%7D%3D%28X%5ETX%2B%5Clambda%20I%29%5E%7B-1%7DX%5ETY%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A&height=214&width=387)

因为S02-线性回归 - 图38为半正定矩阵，则S02-线性回归 - 图39一定为正定矩阵，故一定可逆，有解析解。因此岭回归有抑制过拟合的效果

贝叶斯角度理解

根据贝叶斯学派观点，参数S02-线性回归 - 图40服从一个先验分布，假设该先验分布为S02-线性回归 - 图41#card=math&code=w_i%5Csim%20N%280%2C%5Csigma_0%5E2%29&height=23&width=101)，注意这里指的是单个参数的分布。因为每个参数S02-线性回归 - 图42相互独立，则

S02-线性回归 - 图43%26%3D%5Cprod%7Bi%3D1%7D%5EpP(w_i)%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5Ep%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma0%5E2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7Dw_i%5E2%5Cright)%5C%5C%0A%26%3D%7B1%5Cover(2%5Cpi%5Csigma_0)%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%5Csum%7Bi%3D1%7D%5Epwi%5E2%5Cright)%5C%5C%0A%26%3D%7B1%5Cover(2%5Cpi%5Csigma_0)%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28W%29%26%3D%5Cprod%7Bi%3D1%7D%5EpP%28wi%29%5C%5C%0A%26%3D%5Cprod%7Bi%3D1%7D%5Ep%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma0%5E2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7Dw_i%5E2%5Cright%29%5C%5C%0A%26%3D%7B1%5Cover%282%5Cpi%5Csigma_0%29%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%5Csum%7Bi%3D1%7D%5Epw_i%5E2%5Cright%29%5C%5C%0A%26%3D%7B1%5Cover%282%5Cpi%5Csigma_0%29%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright%29%0A%5Cend%7Baligned%7D%0A&height=238&width=288)

设S02-线性回归 - 图44#card=math&code=%5Cepsilon%5Csim%20N%280%2C%5Csigma%5E2%29&height=23&width=90)，则有S02-线性回归 - 图45%2B%5Cepsilon%3DW%5ETX%2B%5Cepsilon#card=math&code=Y%3Df%28W%29%2B%5Cepsilon%3DW%5ETX%2B%5Cepsilon&height=23&width=194)，显然

S02-线性回归 - 图46%3D(y_i%7CX_i%3BW)%5Csim%20N(W%5ETX_i%2C%5Csigma%5E2)%0A#card=math&code=%28y_i%7CX_i%29%3D%28y_i%7CX_i%3BW%29%5Csim%20N%28W%5ETX_i%2C%5Csigma%5E2%29%0A&height=23&width=273)

根据贝叶斯定理

S02-线性回归 - 图47%26%3D%5Cfrac%7BP(Y%7CX%2CW)P(X%2CW)%7D%7BP(X%2CY)%7D%5C%5C%0A%26%3D%5Cfrac%7BP(Y%7CX%2CW)P(X)P(W)%7D%7BP(X%2CY)%7D%5C%5C%0A%26%3D%5Cfrac%7BP(Y%7CX%2CW)P(W)%7D%7BP(Y%7CX)%7D%5C%5C%0A%26%5Cpropto%20P(Y%7CX%2CW)P(W)%5C%5C%0A%26%3DP(W)%5Cprod%7Bi%3D1%7D%5ENP(y_i%7CX_i%2CW)%5C%5C%0A%26%3D%7B1%5Cover(2%5Cpi%5Csigma_0)%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright)%5Cprod%7Bi%3D1%7D%5EN%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D(yi-W%5ETX_i)%5E2%5Cright)%5C%5C%0A%26%5Cpropto%5Cexp%5Cleft(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%5Csum%7Bi%3D1%7D%5EN(yi-W%5ETX_i)%5E2-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright)%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0AW%7BMAP%7D%26%3D%5Carg%5CmaxW%20%5Clog%20P(W%7CX%2CY)%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Cleft(-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%5Csum%7Bi%3D1%7D%5EN(yi-W%5ETX_i)%5E2-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright)%5C%5C%0A%26%3D%5Carg%5Cmin_W%5Cleft(%5Csum%7Bi%3D1%7D%5EN(W%5ETXi-y_i)%5E2%2B%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma_0%5E2%7DW%5ETW%5Cright)%5C%5C%0A%26%5CLeftrightarrow%5Carg%5Cmin_W%5BL(W)%2B%5Clambda%20P(W)%5D%2C%5Clambda%3D%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma_0%5E2%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Cbegin%7Baligned%7D%0AP%28W%7CX%2CY%29%26%3D%5Cfrac%7BP%28Y%7CX%2CW%29P%28X%2CW%29%7D%7BP%28X%2CY%29%7D%5C%5C%0A%26%3D%5Cfrac%7BP%28Y%7CX%2CW%29P%28X%29P%28W%29%7D%7BP%28X%2CY%29%7D%5C%5C%0A%26%3D%5Cfrac%7BP%28Y%7CX%2CW%29P%28W%29%7D%7BP%28Y%7CX%29%7D%5C%5C%0A%26%5Cpropto%20P%28Y%7CX%2CW%29P%28W%29%5C%5C%0A%26%3DP%28W%29%5Cprod%7Bi%3D1%7D%5ENP%28yi%7CX_i%2CW%29%5C%5C%0A%26%3D%7B1%5Cover%282%5Cpi%5Csigma_0%29%5E%7Bp%5Cover2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright%29%5Cprod%7Bi%3D1%7D%5EN%7B1%5Cover%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%28yi-W%5ETX_i%29%5E2%5Cright%29%5C%5C%0A%26%5Cpropto%5Cexp%5Cleft%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%5Csum%7Bi%3D1%7D%5EN%28yi-W%5ETX_i%29%5E2-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright%29%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%26%5Cbegin%7Baligned%7D%0AW%7BMAP%7D%26%3D%5Carg%5CmaxW%20%5Clog%20P%28W%7CX%2CY%29%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Cleft%28-%7B1%5Cover%7B2%5Csigma%5E2%7D%7D%5Csum%7Bi%3D1%7D%5EN%28yi-W%5ETX_i%29%5E2-%7B1%5Cover%7B2%5Csigma_0%5E2%7D%7D%7C%7CW%7C%7C%5E2%5Cright%29%5C%5C%0A%26%3D%5Carg%5Cmin_W%5Cleft%28%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%2B%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma_0%5E2%7DW%5ETW%5Cright%29%5C%5C%0A%26%5CLeftrightarrow%5Carg%5Cmin_W%5BL%28W%29%2B%5Clambda%20P%28W%29%5D%2C%5Clambda%3D%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma_0%5E2%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A&height=549&width=610)

故加入了L2正则化项的最小二乘估计等价于先验分布和噪声均为高斯分布的最大后验估计。注意这里先验分布和噪声分布的均值都为0

几何意义

考虑如下有约束条件的优化问题

S02-线性回归 - 图48%3D%5Carg%5CminW%5Csum%7Bi%3D1%7D%5EN(W%5ETXi-y_i)%5E2%5C%5C%0As.t.%5Cquad%7C%7CW%7C%7C%5E2%5Cle%20t%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Chat%7BW%7D%3D%5Carg%5Cmin_W%20L%28W%29%3D%5Carg%5Cmin_W%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%5C%5C%0As.t.%5Cquad%7C%7CW%7C%7C%5E2%5Cle%20t%0A%5Cend%7Bgathered%7D%0A&height=78&width=351)

利用拉格朗日乘子法转化为无约束条件的优化问题，即

S02-线性回归 - 图49%3D%5Csum%7Bi%3D1%7D%5EN(W%5ETX_i-y_i)%5E2%2B%5Clambda%7C%7CW%7C%7C%5E2-%5Clambda%20t%0A#card=math&code=J%28W%2C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%28W%5ETX_i-y_i%29%5E2%2B%5Clambda%7C%7CW%7C%7C%5E2-%5Clambda%20t%0A&height=53&width=319)

在给定S02-线性回归 - 图50和S02-线性回归 - 图51后该优化任务与加入了L2正则化的最小二乘估计等价
假设S02-线性回归 - 图52即在二维情况下，S02-线性回归 - 图53%5ET#card=math&code=W%3D%28w1%2Cw_2%29%5ET&height=23&width=110)，![](https://g.yuque.com/gr/latex?X_i%3D(x%7Bi1%7D%2Cx%7Bi2%7D)%5ET#card=math&code=X_i%3D%28x%7Bi1%7D%2Cx_%7Bi2%7D%29%5ET&height=23&width=115)上述有约束条件的优化问题可以写为

S02-线性回归 - 图54%26%3D%5Csum%7Bi%3D1%7D%5EN(W%5ETX_i-y_i)%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5E2%5Cleft(%5Cbegin%7Bpmatrix%7Dw1%26w_2%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7Dx%7Bi1%7D%5C%5Cx%7Bi2%7D%5Cend%7Bpmatrix%7D-y_i%5Cright)%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5E2(w1x%7Bi1%7D%2Bw2x%7Bi2%7D-yi)%5E2%5C%5C%0A%26%3Daw_1%5E2%2Bbw_2%5E2%2Bcw_1%2Bdw_2%2Be%0A%5Cend%7Baligned%7D%5C%5C%0A%E5%85%B6%E4%B8%ADa%2Cb%2Cc%E4%B8%BAx%7Bi1%7D%2Cx%7Bi2%7D%2Cy_i%E6%9E%84%E6%88%90%E7%9A%84%E7%B3%BB%E6%95%B0(i%3D1%2C2%5Ccdots%2CN)%2C%E5%9D%87%E4%B8%BA%E5%B8%B8%E6%95%B0%5C%5C%0As.t.%5Cquad%20w_1%5E2%2Bw_2%5E2%5Cle%20t%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cbegin%7Baligned%7D%0AL%28W%29%26%3D%5Csum%7Bi%3D1%7D%5EN%28W%5ETXi-y_i%29%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5E2%5Cleft%28%5Cbegin%7Bpmatrix%7Dw1%26w_2%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7Dx%7Bi1%7D%5C%5Cx%7Bi2%7D%5Cend%7Bpmatrix%7D-y_i%5Cright%29%5E2%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5E2%28w1x%7Bi1%7D%2Bw2x%7Bi2%7D-yi%29%5E2%5C%5C%0A%26%3Daw_1%5E2%2Bbw_2%5E2%2Bcw_1%2Bdw_2%2Be%0A%5Cend%7Baligned%7D%5C%5C%0A%E5%85%B6%E4%B8%ADa%2Cb%2Cc%E4%B8%BAx%7Bi1%7D%2Cx_%7Bi2%7D%2Cy_i%E6%9E%84%E6%88%90%E7%9A%84%E7%B3%BB%E6%95%B0%28i%3D1%2C2%5Ccdots%2CN%29%2C%E5%9D%87%E4%B8%BA%E5%B8%B8%E6%95%B0%5C%5C%0As.t.%5Cquad%20w_1%5E2%2Bw_2%5E2%5Cle%20t%0A%5Cend%7Bgathered%7D%0A&height=235&width=424)

这是一个凸优化问题，显然S02-线性回归 - 图55#card=math&code=L%28W%29&height=20&width=41)在坐标S02-线性回归 - 图56平面内的投影为一簇椭圆，在没有约束条件时椭圆圆心时S02-线性回归 - 图57#card=math&code=L%28W%29&height=20&width=41)取得最小值。约束条件将S02-线性回归 - 图58限制在一个圆内，画出图像如下，S02-线性回归 - 图59#card=math&code=L%28W%29&height=20&width=41)在椭圆与圆的切点S02-线性回归 - 图60处取得最小值
S02-线性回归 - 图61
假设我们用梯度下降法来求解这个优化问题，考虑某一步到达了约束条件边界的一个点S02-线性回归 - 图62。如果没有约束条件，那么应该按照S02-线性回归 - 图63#card=math&code=%5Cnabla%20J%28W%29&height=20&width=55)即梯度方向迭代，但是在有约束条件的情况下，如图所示，应该按蓝色箭头方向迭代，即约束圆的切线方向，最终收敛于最优解S02-线性回归 - 图64，此时梯度方向与约束圆的法线方向相同

代数解释

假设用梯度下降法来求解这个优化问题时，迭代公式为

S02-线性回归 - 图65%5C%5C%0A%26%3DWt-%5Ceta%5Cnabla(L(W_t)%2B%5Clambda%20W_t%5ETW_t)%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%20L(W_t)-%5Clambda%20W_t%5C%5C%0A%26%3D(1-%5Ceta%5Clambda)W_t-%5Ceta%5Cnabla%20L(W_t)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AW%7Bt%2B1%7D%26%3DW_t-%5Ceta%5Cnabla%20J%28W_t%29%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%28L%28W_t%29%2B%5Clambda%20W_t%5ETW_t%29%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%20L%28W_t%29-%5Clambda%20W_t%5C%5C%0A%26%3D%281-%5Ceta%5Clambda%29W_t-%5Ceta%5Cnabla%20L%28W_t%29%0A%5Cend%7Baligned%7D%0A&height=90&width=269)

该式表明每次迭代后S02-线性回归 - 图66相比S02-线性回归 - 图67降低了一个比例，即在迭代过程中让权重趋向于按比例衰减，因此L2正则化对应权值衰减(Weight Decay)

L1正则化

Lasso推导

推导与L2正则化类似，此处省略

贝叶斯角度解释

推导与L2正则化类似，此处直接给出结论：加入了L1正则化项的最小二乘估计等价于先验分布为拉普拉斯分布和噪声为高斯分布的最大后验估计。注意这里先验分布和噪声分布的均值都为0

几何意义

L1正则化时S02-线性回归 - 图68限制在如图的一个菱形内，显然在点S02-线性回归 - 图69时S02-线性回归 - 图70#card=math&code=L%28W%29&height=20&width=41)取得最小值。此时S02-线性回归 - 图71
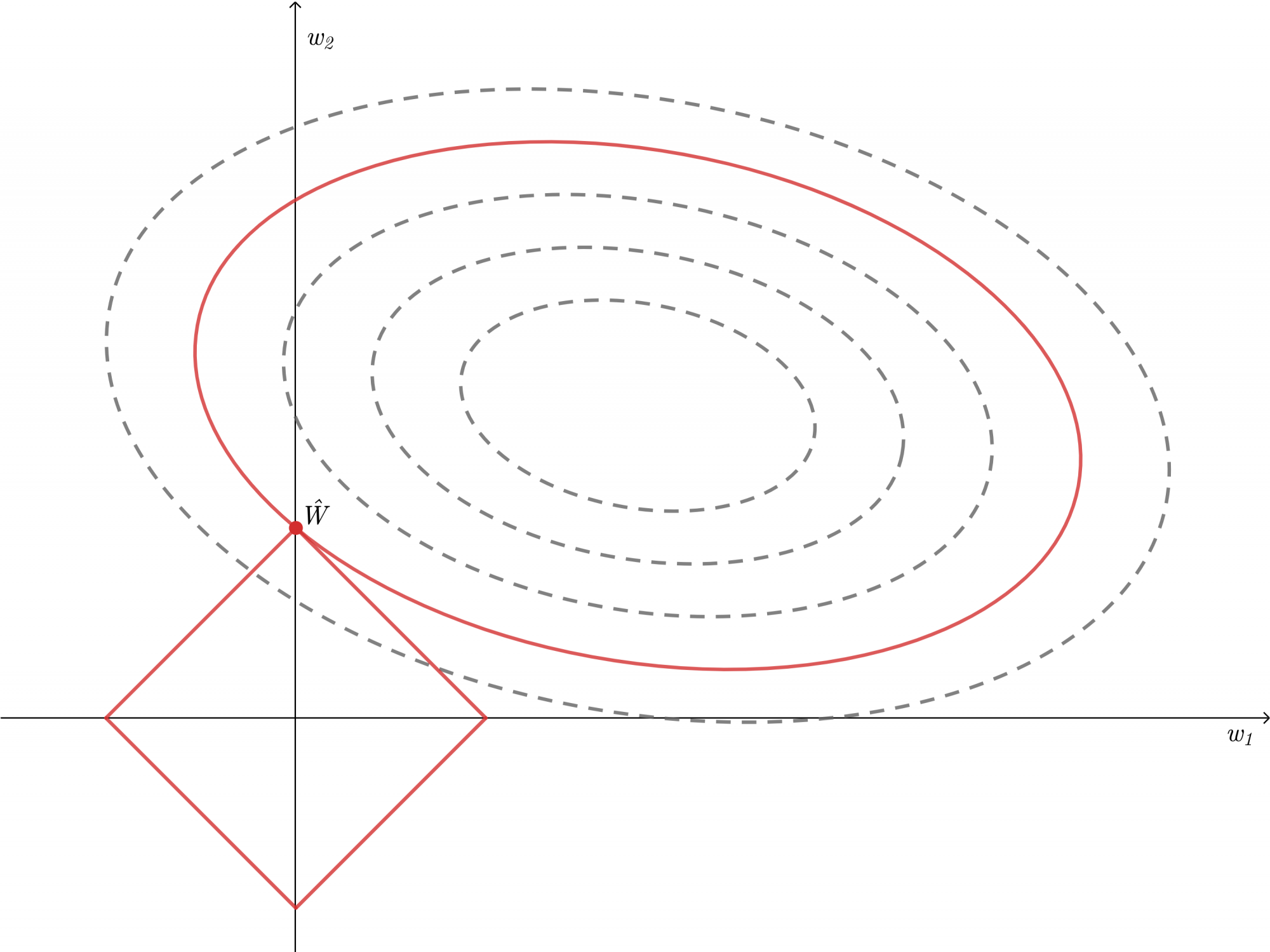
S02-线性回归 - 图72
因此L1正则化倾向于得到稀疏的S02-线性回归 - 图73，即L1正则化会使得部分参数为零。这样就达到了特征选择的效果，可以用来降维，从而抑制了过拟合

代数解释

S02-线性回归 - 图74%5C%5C%0A%26%3DWt-%5Ceta%5Cnabla(L(W_t)%2B%5Clambda%20W_t)%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%20L(W_t)-%5Clambda%5C%5C%0A%26%3D(W_t-%5Clambda)-%5Ceta%5Cnabla%20L(W_t)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AW%7Bt%2B1%7D%26%3DW_t-%5Ceta%5Cnabla%20J%28W_t%29%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%28L%28W_t%29%2B%5Clambda%20W_t%29%5C%5C%0A%26%3DW_t-%5Ceta%5Cnabla%20L%28W_t%29-%5Clambda%5C%5C%0A%26%3D%28W_t-%5Clambda%29-%5Ceta%5Cnabla%20L%28W_t%29%0A%5Cend%7Baligned%7D%0A&height=90&width=241)

该式表明每次迭代后S02-线性回归 - 图75相比S02-线性回归 - 图76有一个偏移量，即在迭代过程中让权重趋向于减少甚至为零，因此L1正则化倾向于让权值稀疏化

总结

  • L1、L2正则化都能达到抑制过拟合的效果
  • L1正则化趋向于得到稀疏化权值，L2正则化趋向于权值衰减但是不会稀疏化权值
  • L1正则化可以用来特征选择和降维