白板推导 - S01-高斯分布 - 《机器学习》

高斯分布
- 1. 高斯分布与极大似然估计
  - 数学推导部分
    - 1. 一维情况
    - 2. 高维情况
  - 高斯分布局限性
- 2. 高斯分布相关概率分布求解
  - 求边缘概率及条件概率
    - 边缘概率
    - 条件概率
  - 求联合高斯概率分布
    - Y的概率分布
    - 联合概率分布

高斯分布

1. 高斯分布与极大似然估计

数学推导部分

给定包含N个d维样本的数据集 $S01-高斯分布 - 图1$ %5ET%3D%0A%5Cbegin%7Bpmatrix%7D%0AX1%5ET%5C%5C%0AX_2%5ET%5C%5C%0A%5Cvdots%5C%5C%0AX_N%5ET%0A%5Cend%7Bpmatrix%7D%7BN%5Ctimes%20d%7D%0A#card=math&code=Data%3AX%3D%28X1%2CX_2%2C%5Cldots%2CX_N%29%5ET%3D%0A%5Cbegin%7Bpmatrix%7D%0AX_1%5ET%5C%5C%0AX_2%5ET%5C%5C%0A%5Cvdots%5C%5C%0AX_N%5ET%0A%5Cend%7Bpmatrix%7D%7BN%5Ctimes%20d%7D%0A)

其中 $S01-高斯分布 - 图2$ 且 $S01-高斯分布 - 图3$ #card=math&code=X_i%5Cmathop%7B%5Csim%7D%5Climits%5E%7Biid%7DN%28%5Cmu%2C%5CSigma%29)，则参数 $S01-高斯分布 - 图4$ #card=math&code=%5Ctheta%3D%28%5Cmu%2C%5CSigma%29)

极大似然估计为 $S01-高斯分布 - 图5$ #card=math&code=%5Ctheta%3D%5Carg%5Cmax%5Climits_%7B%5Ctheta%7DP%28X%7C%5Ctheta%29)

1. 一维情况

讨论 $S01-高斯分布 - 图6$ 的简单情况，即 $S01-高斯分布 - 图7$ #card=math&code=%5Ctheta%3D%28%5Cmu%2C%5Csigma%5E2%29)，此时 $S01-高斯分布 - 图8$ %3D%7B1%5Cover%20%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D(Xi-%5Cmu)%5E2%5D#card=math&code=p%28X_i%7C%5Ctheta%29%3D%7B1%5Cover%20%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D%28X_i-%5Cmu%29%5E2%5D)
而 $S01-高斯分布 - 图9$ %3D%5Cprod%5Climits%7Bi%3D1%7D%5E%7BN%7Dp(Xi%7C%5Ctheta)#card=math&code=P%28X%7C%5Ctheta%29%3D%5Cprod%5Climits%7Bi%3D1%7D%5E%7BN%7Dp%28Xi%7C%5Ctheta%29)，为简化计算，对 $S01-高斯分布 - 图10$ 取对数，则有 $S01-高斯分布 - 图11$ %7D%26%3D%5Clog%5Cprod%5Climits%7Bi%3D1%7D%5EN%7B1%5Cover%20%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D(Xi-%5Cmu)%5E2%5D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Clog%7B1%5Cover%20%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D(Xi-%5Cmu)%5E2%5D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5B%5Clog%7B1%5Cover%20%5Csqrt%7B2%5Cpi%7D%7D%2B%5Clog%7B1%5Cover%20%5Csigma%7D-%5Cfrac%7B(Xi-%5Cmu)%5E2%7D%7B2%5Csigma%5E2%7D%5D%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Clog%7BP%28X%7C%5Ctheta%29%7D%26%3D%5Clog%5Cprod%5Climits%7Bi%3D1%7D%5EN%7B1%5Cover%20%5Csqrt%7B2%5Cpi%5Csigma%5E2%7D%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D%28Xi-%5Cmu%29%5E2%5D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Clog%7B1%5Cover%20%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cexp%5B-%7B1%5Cover%202%5Csigma%5E2%7D%28Xi-%5Cmu%29%5E2%5D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5B%5Clog%7B1%5Cover%20%5Csqrt%7B2%5Cpi%7D%7D%2B%5Clog%7B1%5Cover%20%5Csigma%7D-%5Cfrac%7B%28X_i-%5Cmu%29%5E2%7D%7B2%5Csigma%5E2%7D%5D%5C%5C%0A%5Cend%7Baligned%7D%0A)

求 $S01-高斯分布 - 图12$ 和 $S01-高斯分布 - 图13$ #card=math&code=E%28%5Cmu_%7BMLE%7D%29)

$S01-高斯分布 - 图14$ %7D%5C%5C%0A%26%3D%5Carg%5Cmin%5Cmu%5Csum%5Climits%7Bi%3D1%7D%5EN(Xi-%5Cmu)%5E2%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cmu%7BMLE%7D%26%3D%5Carg%5Cmax%5Cmu%5Clog%7BP%28X%7C%5Ctheta%29%7D%5C%5C%0A%26%3D%5Carg%5Cmin%5Cmu%5Csum%5Climits%7Bi%3D1%7D%5EN%28X_i-%5Cmu%29%5E2%0A%5Cend%7Baligned%7D%0A)
![](https://g.yuque.com/gr/latex?%5Cbegin%7Baligned%7D%0A%26%7B%5Cpartial%5Cover%20%5Cpartial%5Cmu%7D%5Csum%5Climits%7Bi%3D1%7D%5EN(Xi-%5Cmu)%5E2%3D0%5C%5C%0A%26%5CRightarrow%5Csum%5Climits%7Bi%3D1%7D%5EN2(%5Cmu-Xi)%3D0%5C%5C%0A%26%5CRightarrow%5Cmu%7BMLE%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5C%5C%0A%5C%5C%0AE(%5Cmu%7BMLE%7D)%26%3DE%5Cleft(%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5Cright)%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENE%5Cleft(Xi%5Cright)%7D%7BN%7D%5C%5C%0A%26%3D%5Cmu%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%7B%5Cpartial%5Cover%20%5Cpartial%5Cmu%7D%5Csum%5Climits%7Bi%3D1%7D%5EN%28Xi-%5Cmu%29%5E2%3D0%5C%5C%0A%26%5CRightarrow%5Csum%5Climits%7Bi%3D1%7D%5EN2%28%5Cmu-Xi%29%3D0%5C%5C%0A%26%5CRightarrow%5Cmu%7BMLE%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5C%5C%0A%5C%5C%0AE%28%5Cmu%7BMLE%7D%29%26%3DE%5Cleft%28%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5Cright%29%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENE%5Cleft%28Xi%5Cright%29%7D%7BN%7D%5C%5C%0A%26%3D%5Cmu%0A%5Cend%7Baligned%7D%0A) ![](https://g.yuque.com/gr/latex?%5Cmu%7BMLE%7D#card=math&code=%5Cmu_%7BMLE%7D) $S01-高斯分布 - 图15$

求 $S01-高斯分布 - 图16$ 和 $S01-高斯分布 - 图17$ #card=math&code=E%28%5Csigma%7BMLE%7D%5E2%29)![](https://g.yuque.com/gr/latex?%5Cbegin%7Baligned%7D%0A%5Csigma%7BMLE%7D%26%3D%5Carg%5Cmax%5Csigma%5Clog%7BP(X%7C%5Ctheta)%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Csigma%5Csum%5Climits%7Bi%3D1%7D%5EN%5B-%5Clog%5Csigma-%5Cfrac%7B(X_i-%5Cmu)%5E2%7D%7B2%5Csigma%5E2%7D%5D%5C%5C%0A%26%3D%5Carg%5Cmax%5Csigma%7BL(%5Csigma)%7D%5C%5C%0A%5C%5C%0A%5Cfrac%7B%5Cpartial%7BL(%5Csigma)%7D%7D%7B%5Cpartial%5Csigma%7D%26%3D0%5C%5C%0A%26%5CRightarrow%5Csum%5Climits%7Bi%3D1%7D%5EN%5B%5Cfrac%7B(X_i-%5Cmu)%5E2%7D%7B%5Csigma%5E3%7D-%7B1%5Cover%5Csigma%7D%5D%3D0%5C%5C%0A%26%5CRightarrow%5Csigma%7BMLE%7D%5E2%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cfrac%7B(X_i-%5Cmu)%5E2%7D%7BN%7D%5C%5C%0A%26%5CRightarrow%5Csigma%7BMLE%7D%5E2%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN(X_i-%5Cmu%7BMLE%7D)%5E2%7D%7BN%7D%5C%5C%0A%5C%5C%0A%5Csigma%7BMLE%7D%5E2%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN(Xi-%5Cmu%7BMLE%7D)%5E2%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN(X_i%5E2-2%5Cmu%7BMLE%7DXi%2B%5Cmu%7BMLE%7D%5E2)%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%5E2%7D%7BN%7D-2%5Cmu%7BMLE%7D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%2B%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cmu%7BMLE%7D%5E2%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENXi%5E2%7D%7BN%7D-%5Cmu%7BMLE%7D%5E2%5C%5C%0A%5C%5C%0AE(%5Csigma%7BMLE%7D%5E2)%26%3DE%5Cleft(%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENXi%5E2%7D%7BN%7D-%5Cmu%7BMLE%7D%5E2%5Cright)%5C%5C%0A%26%3DE%5Cleft((%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%5E2%7D%7BN%7D-%5Cmu%5E2)-(%5Cmu%7BMLE%7D%5E2-%5Cmu%5E2)%5Cright)%5C%5C%0A%26%3DE%5Cleft(%5Cfrac%7B%5Csum%7Bi%3D1%7D%5EN(X_i%5E2-%5Cmu%5E2)%7D%7BN%7D%5Cright)-E(%5Cmu%7BMLE%7D%5E2-%5Cmu%5E2)%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENE(X_i%5E2-%5Cmu%5E2)%7D%7BN%7D-%5BE(%5Cmu%7BMLE%7D%5E2)-E(%5Cmu%5E2)%5D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5EN%5BE(X_i%5E2)-E%5E2(X_i)%5D%7D%7BN%7D-%5BE(%5Cmu%7BMLE%7D%5E2)-E%5E2(%5Cmu%7BMLE%7D)%5D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENVar(Xi)%7D%7BN%7D-Var(%5Cmu%7BMLE%7D)%5C%5C%0A%26%3D%5Csigma%5E2-Var%5Cleft(%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5Cright)%5C%5C%0A%26%3D%5Csigma%5E2-%5Cfrac%7BVar(%5Csum%7Bi%3D1%7D%5ENXi)%7D%7BN%5E2%7D%5C%5C%0A%26%3D%5Csigma%5E2-%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENVar(Xi)%7D%7BN%5E2%7D%5C%5C%0A%26%3D%5Cfrac%7BN-1%7D%7BN%7D%5Csigma%5E2%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Csigma%7BMLE%7D%26%3D%5Carg%5Cmax%5Csigma%5Clog%7BP%28X%7C%5Ctheta%29%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Csigma%5Csum%5Climits%7Bi%3D1%7D%5EN%5B-%5Clog%5Csigma-%5Cfrac%7B%28X_i-%5Cmu%29%5E2%7D%7B2%5Csigma%5E2%7D%5D%5C%5C%0A%26%3D%5Carg%5Cmax%5Csigma%7BL%28%5Csigma%29%7D%5C%5C%0A%5C%5C%0A%5Cfrac%7B%5Cpartial%7BL%28%5Csigma%29%7D%7D%7B%5Cpartial%5Csigma%7D%26%3D0%5C%5C%0A%26%5CRightarrow%5Csum%5Climits%7Bi%3D1%7D%5EN%5B%5Cfrac%7B%28X_i-%5Cmu%29%5E2%7D%7B%5Csigma%5E3%7D-%7B1%5Cover%5Csigma%7D%5D%3D0%5C%5C%0A%26%5CRightarrow%5Csigma%7BMLE%7D%5E2%3D%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cfrac%7B%28X_i-%5Cmu%29%5E2%7D%7BN%7D%5C%5C%0A%26%5CRightarrow%5Csigma%7BMLE%7D%5E2%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%28X_i-%5Cmu%7BMLE%7D%29%5E2%7D%7BN%7D%5C%5C%0A%5C%5C%0A%5Csigma%7BMLE%7D%5E2%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%28Xi-%5Cmu%7BMLE%7D%29%5E2%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%28X_i%5E2-2%5Cmu%7BMLE%7DXi%2B%5Cmu%7BMLE%7D%5E2%29%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%5E2%7D%7BN%7D-2%5Cmu%7BMLE%7D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%2B%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%5Cmu%7BMLE%7D%5E2%7D%7BN%7D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5ENXi%5E2%7D%7BN%7D-%5Cmu%7BMLE%7D%5E2%5C%5C%0A%5C%5C%0AE%28%5Csigma%7BMLE%7D%5E2%29%26%3DE%5Cleft%28%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENXi%5E2%7D%7BN%7D-%5Cmu%7BMLE%7D%5E2%5Cright%29%5C%5C%0A%26%3DE%5Cleft%28%28%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%5E2%7D%7BN%7D-%5Cmu%5E2%29-%28%5Cmu%7BMLE%7D%5E2-%5Cmu%5E2%29%5Cright%29%5C%5C%0A%26%3DE%5Cleft%28%5Cfrac%7B%5Csum%7Bi%3D1%7D%5EN%28X_i%5E2-%5Cmu%5E2%29%7D%7BN%7D%5Cright%29-E%28%5Cmu%7BMLE%7D%5E2-%5Cmu%5E2%29%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENE%28X_i%5E2-%5Cmu%5E2%29%7D%7BN%7D-%5BE%28%5Cmu%7BMLE%7D%5E2%29-E%28%5Cmu%5E2%29%5D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5EN%5BE%28X_i%5E2%29-E%5E2%28X_i%29%5D%7D%7BN%7D-%5BE%28%5Cmu%7BMLE%7D%5E2%29-E%5E2%28%5Cmu%7BMLE%7D%29%5D%5C%5C%0A%26%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENVar%28Xi%29%7D%7BN%7D-Var%28%5Cmu%7BMLE%7D%29%5C%5C%0A%26%3D%5Csigma%5E2-Var%5Cleft%28%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENX_i%7D%7BN%7D%5Cright%29%5C%5C%0A%26%3D%5Csigma%5E2-%5Cfrac%7BVar%28%5Csum%7Bi%3D1%7D%5ENXi%29%7D%7BN%5E2%7D%5C%5C%0A%26%3D%5Csigma%5E2-%5Cfrac%7B%5Csum%7Bi%3D1%7D%5ENVar%28X_i%29%7D%7BN%5E2%7D%5C%5C%0A%26%3D%5Cfrac%7BN-1%7D%7BN%7D%5Csigma%5E2%0A%5Cend%7Baligned%7D%0A)

因此 $S01-高斯分布 - 图18$ 是 $S01-高斯分布 - 图19$ 的有偏估计量， $S01-高斯分布 - 图20$ 无偏估计量为 $S01-高斯分布 - 图21$ %5E2%7D%7BN-1%7D%0A#card=math&code=%7B%5Chat%5Csigma%7D%5E2%3D%5Cfrac%7BN%7D%7BN-1%7D%5Csigma%7BMLE%7D%5E2%3D%5Cfrac%7B%5Csum%5Climits%7Bi%3D1%7D%5EN%28Xi-%5Cmu%7BMLE%7D%29%5E2%7D%7BN-1%7D%0A)

2. 高维情况

对于一个 $S01-高斯分布 - 图22$ %5ET#card=math&code=Xi%3DX%3D%28x_1%2Cx_2%2C%5Cldots%2Cx_d%29%5ET)有 $S01-高斯分布 - 图23$ %7D%3D%7B1%5Cover(2%5Cpi)%5E%7Bd%5Cover2%7D%7B%7C%5CSigma%7C%5E%7B1%5Cover2%7D%7D%7D%5Cexp%5B-%7B1%5Cover2%7D(X-%5Cmu)%5ET%5CSigma%5E%7B-1%7D(X-%5Cmu)%5D%0A#card=math&code=X%5Csim%7BN%28%5Cmu%2C%5CSigma%29%7D%3D%7B1%5Cover%282%5Cpi%29%5E%7Bd%5Cover2%7D%7B%7C%5CSigma%7C%5E%7B1%5Cover2%7D%7D%7D%5Cexp%5B-%7B1%5Cover2%7D%28X-%5Cmu%29%5ET%5CSigma%5E%7B-1%7D%28X-%5Cmu%29%5D%0A)
$S01-高斯分布 - 图24$ %5ET%5C%5C%0A%5C%5C%0A%5CSigma%7Bd%5Ctimes%20d%7D%26%3D%0A%5Cbegin%7Bbmatrix%7D%0A%20%20%5Csigma%7B11%7D%5E2%26%5Csigma%7B12%7D%5E2%26%5Ccdots%26%5Csigma%7B1d%7D%5E2%20%5C%5C%0A%20%20%5Csigma%7B21%7D%5E2%26%5Csigma%7B22%7D%5E2%26%5Ccdots%26%5Csigma%7B2d%7D%5E2%20%5C%5C%0A%20%20%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%20%5C%5C%0A%20%20%5Csigma%7Bd1%7D%5E2%26%5Csigma%7Bd2%7D%5E2%26%5Ccdots%26%5Csigma%7Bdd%7D%5E2%20%5C%5C%0A%5Cend%7Bbmatrix%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cmu%26%3D%28%5Cmu_1%2C%5Cmu_2%2C%5Cldots%2C%5Cmu_d%29%5ET%5C%5C%0A%5C%5C%0A%5CSigma%7Bd%5Ctimes%20d%7D%26%3D%0A%5Cbegin%7Bbmatrix%7D%0A%20%20%5Csigma%7B11%7D%5E2%26%5Csigma%7B12%7D%5E2%26%5Ccdots%26%5Csigma%7B1d%7D%5E2%20%5C%5C%0A%20%20%5Csigma%7B21%7D%5E2%26%5Csigma%7B22%7D%5E2%26%5Ccdots%26%5Csigma%7B2d%7D%5E2%20%5C%5C%0A%20%20%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%20%5C%5C%0A%20%20%5Csigma%7Bd1%7D%5E2%26%5Csigma%7Bd2%7D%5E2%26%5Ccdots%26%5Csigma_%7Bdd%7D%5E2%20%5C%5C%0A%5Cend%7Bbmatrix%7D%0A%5Cend%7Baligned%7D%0A)

$S01-高斯分布 - 图25$ %5ET%5CSigma%5E%7B-1%7D(X-%5Cmu)#card=math&code=%28X-%5Cmu%29%5ET%5CSigma%5E%7B-1%7D%28X-%5Cmu%29)又称为 $S01-高斯分布 - 图26$ 和 $S01-高斯分布 - 图27$ 间的马氏距离

假设 $S01-高斯分布 - 图28$ 为正定矩阵，对其进行特征值分解 $S01-高斯分布 - 图29$ ，其中 $S01-高斯分布 - 图30$ %7Bp%5Ctimes%20p%7D#card=math&code=U%3D%28u_1%2Cu_2%2C%5Cldots%2Cu_d%29%7Bp%5Ctimes%20p%7D)， $S01-高斯分布 - 图31$ ， $S01-高斯分布 - 图32$ #card=math&code=%5CLambda%3Ddiag%28%5Clambda1%2C%5Clambda_2%2C%5Cldots%2C%5Clambda_d%29) $S01-高斯分布 - 图33$ %0A%5Cbegin%7Bpmatrix%7D%0A%5Clambda_1%260%26%5Ccdots%260%5C%5C%0A0%26%5Clambda_2%26%5Ccdots%260%5C%5C%0A%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%5C%5C%0A0%260%26%5Ccdots%26%5Clambda_d%0A%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7Du_1%5ET%5C%5Cu_2%5ET%5C%5C%5Cvdots%5C%5Cu_d%5ET%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D(%5Clambda_1u_1%2C%5Clambda_2u_2%2C%5Ccdots%2C%5Clambda_du_d)%0A%5Cbegin%7Bpmatrix%7Du_1%5ET%5C%5Cu_2%5ET%5C%5C%5Cvdots%5C%5Cu_d%5ET%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%5Clambdaiu_iu_i%5ET%5C%5C%0A%5C%5C%0A%5CSigma%5E%7B-1%7D%26%3D(U%5CLambda%7BU%5ET%7D)%5E%7B-1%7D%3D(U%5ET)%5E%7B-1%7D%5CLambda%5E%7B-1%7DU%5E%7B-1%7D%3DU%5CLambda%5E%7B-1%7DU%5ET%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%7B1%5Cover%5Clambdai%7Du_iu_i%5ET%5C%5C%0A%5C%5C%0A(X-%5Cmu)%5ET%5CSigma%5E%7B-1%7D(X-%5Cmu)%26%3D(X-%5Cmu)%5ET%5Cleft(%5Csum%5Climits%7Bi%3D1%7D%5Ed%7B1%5Cover%5Clambdai%7Du_iu_i%5ET%5Cright)(X-%5Cmu)%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed(X-%5Cmu)%5ETui%7B1%5Cover%5Clambda_i%7Du_i%5ET(X-%5Cmu)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5CSigma%26%3D%28u_1%2Cu_2%2C%5Cldots%2Cu_d%29%0A%5Cbegin%7Bpmatrix%7D%0A%5Clambda_1%260%26%5Ccdots%260%5C%5C%0A0%26%5Clambda_2%26%5Ccdots%260%5C%5C%0A%5Cvdots%26%5Cvdots%26%5Cddots%26%5Cvdots%5C%5C%0A0%260%26%5Ccdots%26%5Clambda_d%0A%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7Du_1%5ET%5C%5Cu_2%5ET%5C%5C%5Cvdots%5C%5Cu_d%5ET%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%28%5Clambda_1u_1%2C%5Clambda_2u_2%2C%5Ccdots%2C%5Clambda_du_d%29%0A%5Cbegin%7Bpmatrix%7Du_1%5ET%5C%5Cu_2%5ET%5C%5C%5Cvdots%5C%5Cu_d%5ET%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%5Clambdaiu_iu_i%5ET%5C%5C%0A%5C%5C%0A%5CSigma%5E%7B-1%7D%26%3D%28U%5CLambda%7BU%5ET%7D%29%5E%7B-1%7D%3D%28U%5ET%29%5E%7B-1%7D%5CLambda%5E%7B-1%7DU%5E%7B-1%7D%3DU%5CLambda%5E%7B-1%7DU%5ET%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%7B1%5Cover%5Clambdai%7Du_iu_i%5ET%5C%5C%0A%5C%5C%0A%28X-%5Cmu%29%5ET%5CSigma%5E%7B-1%7D%28X-%5Cmu%29%26%3D%28X-%5Cmu%29%5ET%5Cleft%28%5Csum%5Climits%7Bi%3D1%7D%5Ed%7B1%5Cover%5Clambdai%7Du_iu_i%5ET%5Cright%29%28X-%5Cmu%29%5C%5C%0A%26%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%28X-%5Cmu%29%5ETu_i%7B1%5Cover%5Clambda_i%7Du_i%5ET%28X-%5Cmu%29%0A%5Cend%7Baligned%7D%0A)

令 $S01-高斯分布 - 图34$ %5ET#card=math&code=Y%3D%28y1%2Cy_2%2C%5Cldots%2Cy_d%29%5ET)，其中 $S01-高斯分布 - 图35$ %5ETu_i#card=math&code=y_i%3D%28X-%5Cmu%29%5ETu_i)， $S01-高斯分布 - 图36$ %5ET%5CSigma%5E%7B-1%7D(X-%5Cmu)#card=math&code=%5CDelta%3D%28X-%5Cmu%29%5ET%5CSigma%5E%7B-1%7D%28X-%5Cmu%29)，则![](https://g.yuque.com/gr/latex?%5CDelta%3D%5Csum%5Climits%7Bi%3D1%7D%5Edyi%7B1%5Cover%5Clambda_i%7Dy_i%5ET%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%7Byi%5E2%5Cover%5Clambda_i%7D%0A#card=math&code=%5CDelta%3D%5Csum%5Climits%7Bi%3D1%7D%5Edyi%7B1%5Cover%5Clambda_i%7Dy_i%5ET%3D%5Csum%5Climits%7Bi%3D1%7D%5Ed%7By_i%5E2%5Cover%5Clambda_i%7D%0A)

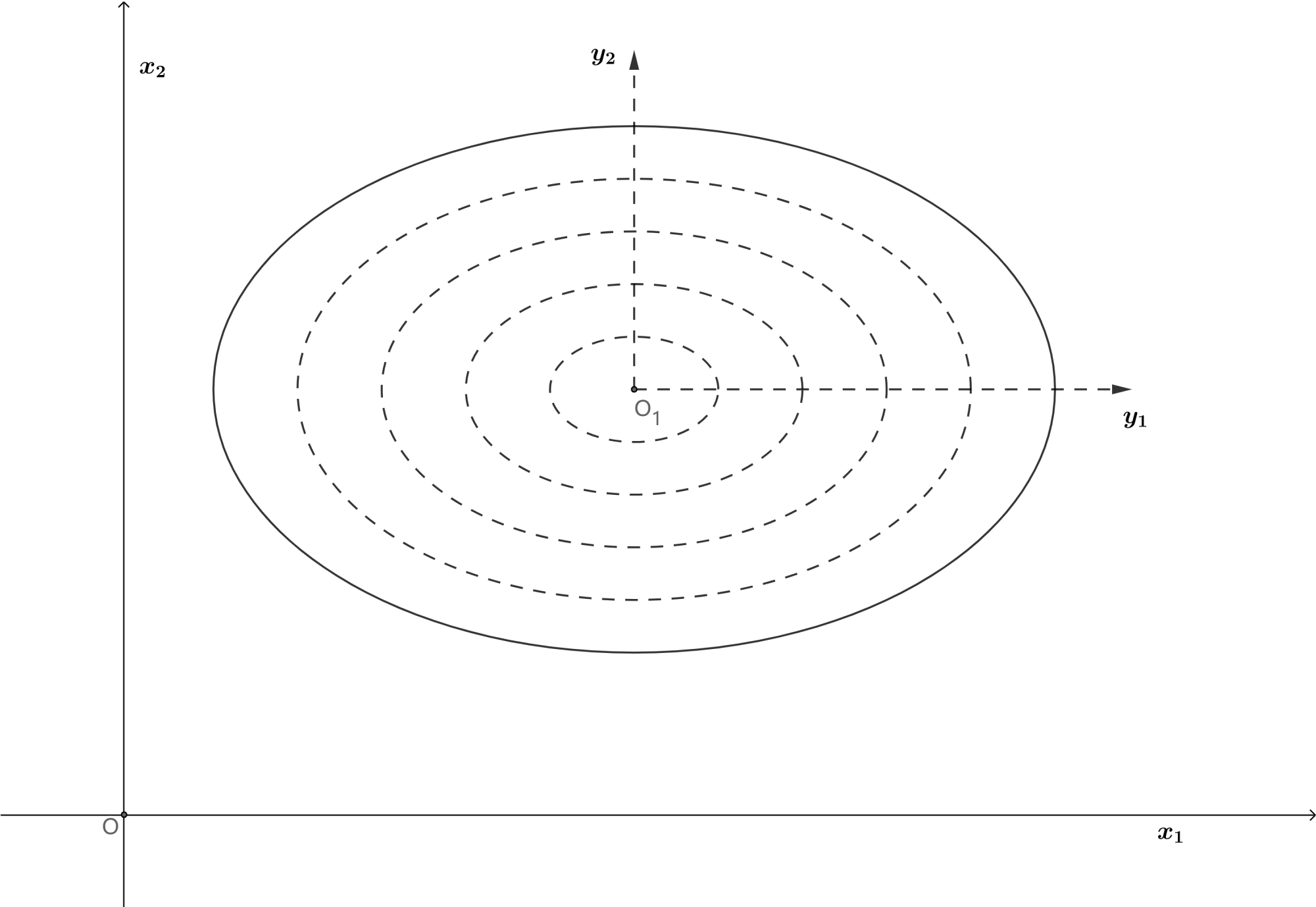
在 $S01-高斯分布 - 图37$ 即2维情况下， $S01-高斯分布 - 图38$ 。在给定 $S01-高斯分布 - 图39$ 值时，马氏距离即为一个在 $S01-高斯分布 - 图40$ 坐标轴下的椭圆。显然 $S01-高斯分布 - 图41$ 为 $S01-高斯分布 - 图42$ 在 $S01-高斯分布 - 图43$ 上的投影，那么特征值分解相当于对X做了坐标转换到Y坐标系。当 $S01-高斯分布 - 图44$ 值变化时，马氏距离即为在平面上的一簇椭圆，也即高斯分布三维图像平行于X平面的横截面的投影

高斯分布局限性

参数很多，d维高斯分布需要参数个数为 $S01-高斯分布 - 图46$ %7D%7B2%7D%3DO(d%5E2)#card=math&code=%5Cfrac%7Bd%28d%2B1%29%7D%7B2%7D%3DO%28d%5E2%29)。因此实际使用中会对协方差矩阵 $S01-高斯分布 - 图47$ 进行简化，假设 $S01-高斯分布 - 图48$ 为对角矩阵，那么就不需要进行特征值分解，此时图像为两个轴与X坐标系平行的椭圆。进一步如果假设 $S01-高斯分布 - 图49$ 对角矩阵的 $S01-高斯分布 - 图50$ 都相等，则图像为一个圆，此时又称X为各向同性的高斯分布
实际的数据分布可能不符合高斯分布，因此需要对单纯的高斯分布模型进行变化，例如高斯混合模型(GMM)

2. 高斯分布相关概率分布求解

求边缘概率及条件概率

令 $S01-高斯分布 - 图52$ #card=math&code=X%3D%5Cbegin%7Bpmatrix%7DXa%5C%5CX_b%5Cend%7Bpmatrix%7D%2CX_a%5Cin%5Cmathbb%7BR%7D%5Em%2CX_b%5Cin%5Cmathbb%7BR%7D%5En%2Cm%2Bn%3Dd%2CP%28X%29)即为 $S01-高斯分布 - 图53$ 和 $S01-高斯分布 - 图54$ 的联合概率分布
$S01-高斯分布 - 图55$
![](https://g.yuque.com/gr/latex?%E4%BB%A4%5CSigma%3D%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%2C%5CSigma%7Baa%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bm%5Ctimes%20m%7D%2C%5CSigma%7Bab%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bm%5Ctimes%20n%7D%2C%5CSigma%7Bba%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bn%5Ctimes%20m%7D%2C%5CSigma%7Bbb%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bn%5Ctimes%20n%7D#card=math&code=%E4%BB%A4%5CSigma%3D%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%2C%5CSigma%7Baa%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bm%5Ctimes%20m%7D%2C%5CSigma%7Bab%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bm%5Ctimes%20n%7D%2C%5CSigma%7Bba%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bn%5Ctimes%20m%7D%2C%5CSigma_%7Bbb%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bn%5Ctimes%20n%7D)

边缘概率

$S01-高斯分布 - 图56$ %26%3D%0A%5Cbegin%7Bpmatrix%7DIm%260%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5Cmu_a%5C%5C%5Cmu_b%5Cend%7Bpmatrix%7D%0A%3D%5Cmu_a%5C%5C%0A%5CSigma(X_a)%26%3D%0A%5Cbegin%7Bpmatrix%7DI_m%260%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DI_m%5C%5C0%5Cend%7Bpmatrix%7D%0A%3D%5CSigma%7Baa%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AXa%26%3D%0A%5Cbegin%7Bpmatrix%7DI_m%260%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DX_a%5C%5CX_b%5Cend%7Bpmatrix%7D%5C%5C%0A%5CRightarrow%20E%28X_a%29%26%3D%0A%5Cbegin%7Bpmatrix%7DI_m%260%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5Cmu_a%5C%5C%5Cmu_b%5Cend%7Bpmatrix%7D%0A%3D%5Cmu_a%5C%5C%0A%5CSigma%28X_a%29%26%3D%0A%5Cbegin%7Bpmatrix%7DI_m%260%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DI_m%5C%5C0%5Cend%7Bpmatrix%7D%0A%3D%5CSigma%7Baa%7D%0A%5Cend%7Baligned%7D%0A)

$S01-高斯分布 - 图57$ %7D%EF%BC%8C%E5%90%8C%E7%90%86Xb%5Csim%7BN(%5Cmu_b%2C%5CSigma%7Bbb%7D)%7D#card=math&code=%E6%95%85Xa%5Csim%7BN%28%5Cmu_a%2C%5CSigma%7Baa%7D%29%7D%EF%BC%8C%E5%90%8C%E7%90%86Xb%5Csim%7BN%28%5Cmu_b%2C%5CSigma%7Bbb%7D%29%7D)

条件概率

$S01-高斯分布 - 图58$

$S01-高斯分布 - 图59$ %26%3D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26In%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5Cmu_a%5C%5C%5Cmu_b%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%5Cmu_b-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%5Cmu_a%5C%5C%0A%E8%AE%B0%E4%BD%9C%5Cmu%7Bb%5Ccdot%20a%7D%5C%5C%0A%5C%5C%0A%5CRightarrow%20Var(X%7Bb%5Ccdot%20a%7D)%26%3D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26I_n%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26I_n%5Cend%7Bpmatrix%7D%5ET%5C%5C%0A%26%3D%5CSigma%7Bbb%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%5CSigma%7Bab%7D%5C%5C%0A%E8%AE%B0%E4%BD%9C%5CSigma%7Bbb%5Ccdot%20a%7D%5C%5C%0A%5C%5C%0A%5CRightarrow%20E(Xb%7CX_a)%26%3DE(X_b)%5C%5C%0A%26%3DE(X%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa)%5C%5C%0A%26%3DE(X%7Bb%5Ccdot%20a%7D)%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%5C%5C%0A%26%3D%5Cmu%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%5C%5C%0A%5C%5C%0A%5CSigma(X_b%7CX_a)%26%3D%5CSigma(X_b)%5C%5C%0A%26%3D%5CSigma(X%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa)%5C%5C%0A%26%3D%5CSigma(X%7Bb%5Ccdot%20a%7D)%5C%5C%0A%26%3D%5CSigma%7Bbb%5Ccdot%20a%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AX%7Bb%5Ccdot%20a%7D%26%3D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26In%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7DX_a%5C%5CX_b%5Cend%7Bpmatrix%7D%5C%5C%0A%5CRightarrow%20E%28X%7Bb%5Ccdot%20a%7D%29%26%3D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26In%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5Cmu_a%5C%5C%5Cmu_b%5Cend%7Bpmatrix%7D%5C%5C%0A%26%3D%5Cmu_b-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%5Cmu_a%5C%5C%0A%E8%AE%B0%E4%BD%9C%5Cmu%7Bb%5Ccdot%20a%7D%5C%5C%0A%5C%5C%0A%5CRightarrow%20Var%28X%7Bb%5Ccdot%20a%7D%29%26%3D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26I_n%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D%5CSigma%7Baa%7D%26%5CSigma%7Bab%7D%5C%5C%5CSigma%7Bba%7D%26%5CSigma%7Bbb%7D%5Cend%7Bpmatrix%7D%0A%5Cbegin%7Bpmatrix%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%26I_n%5Cend%7Bpmatrix%7D%5ET%5C%5C%0A%26%3D%5CSigma%7Bbb%7D-%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7D%5CSigma%7Bab%7D%5C%5C%0A%E8%AE%B0%E4%BD%9C%5CSigma%7Bbb%5Ccdot%20a%7D%5C%5C%0A%5C%5C%0A%5CRightarrow%20E%28Xb%7CX_a%29%26%3DE%28X_b%29%5C%5C%0A%26%3DE%28X%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%29%5C%5C%0A%26%3DE%28X%7Bb%5Ccdot%20a%7D%29%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%5C%5C%0A%26%3D%5Cmu%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%5C%5C%0A%5C%5C%0A%5CSigma%28X_b%7CX_a%29%26%3D%5CSigma%28X_b%29%5C%5C%0A%26%3D%5CSigma%28X%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%29%5C%5C%0A%26%3D%5CSigma%28X%7Bb%5Ccdot%20a%7D%29%5C%5C%0A%26%3D%5CSigma_%7Bbb%5Ccdot%20a%7D%0A%5Cend%7Baligned%7D%0A)

$S01-高斯分布 - 图60$ %EF%BC%8C%E5%90%8C%E7%90%86Xa%7CX_b%5Csim%20N(%5Cmu%7Ba%5Ccdot%20b%7D%2B%5CSigma%7Bab%7D%5CSigma%7Bbb%7D%5E%7B-1%7DXb%2C%5CSigma%7Baa%5Ccdot%20b%7D)#card=math&code=%E6%95%85Xb%7CX_a%5Csim%20N%28%5Cmu%7Bb%5Ccdot%20a%7D%2B%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7DXa%2C%5CSigma%7Bbb%5Ccdot%20a%7D%29%EF%BC%8C%E5%90%8C%E7%90%86Xa%7CX_b%5Csim%20N%28%5Cmu%7Ba%5Ccdot%20b%7D%2B%5CSigma%7Bab%7D%5CSigma%7Bbb%7D%5E%7B-1%7DXb%2C%5CSigma%7Baa%5Ccdot%20b%7D%29)

求联合高斯概率分布

设随机变量 $S01-高斯分布 - 图61$ 的概率分布 $S01-高斯分布 - 图62$ %2CP(Y%7CX)#card=math&code=P%28X%29%2CP%28Y%7CX%29)满足

$S01-高斯分布 - 图63$ %26%3DN(X%7C%5Cmu%2C%5CLambda%5E%7B-1%7D)%5C%5C%0AP(Y%7CX)%26%3DN(Y%7CAX%2Bb%2CL%5E%7B-1%7D)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28X%29%26%3DN%28X%7C%5Cmu%2C%5CLambda%5E%7B-1%7D%29%5C%5C%0AP%28Y%7CX%29%26%3DN%28Y%7CAX%2Bb%2CL%5E%7B-1%7D%29%0A%5Cend%7Baligned%7D%0A)

那么 $S01-高斯分布 - 图64$ #card=math&code=Y%3DAX%2Bb%2B%5Cepsilon%2C%5Cepsilon%5Csim%20N%280%2CL%5E%7B-1%7D%29)即可满足上述分布

Y的概率分布

$S01-高斯分布 - 图65$ %26%3DE(AX%2Bb%2B%5Cepsilon)%5C%5C%0A%26%3DAE(X)%2Bb%2BE(%5Cepsilon)%5C%5C%0A%26%3DA%5Cmu%2Bb%5C%5C%0A%5C%5C%0A%5CSigma(Y)%26%3D%5CSigma(AX%2BB%2B%5Cepsilon)%5C%5C%0A%26%3D%5CSigma(AX)%2B%5CSigma(%5Cepsilon)%5C%5C%0A%26%3DA%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AE%28Y%29%26%3DE%28AX%2Bb%2B%5Cepsilon%29%5C%5C%0A%26%3DAE%28X%29%2Bb%2BE%28%5Cepsilon%29%5C%5C%0A%26%3DA%5Cmu%2Bb%5C%5C%0A%5C%5C%0A%5CSigma%28Y%29%26%3D%5CSigma%28AX%2BB%2B%5Cepsilon%29%5C%5C%0A%26%3D%5CSigma%28AX%29%2B%5CSigma%28%5Cepsilon%29%5C%5C%0A%26%3DA%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%0A%5Cend%7Baligned%7D%0A)

故 $S01-高斯分布 - 图66$ #card=math&code=Y%5Csim%20N%28A%5Cmu%2Bb%2CA%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%29)

联合概率分布

令 $S01-高斯分布 - 图67$ ， $S01-高斯分布 - 图68$ #card=math&code=P%28Z%29)即为 $S01-高斯分布 - 图69$ 和 $S01-高斯分布 - 图70$ 的联合概率分布，则有

$S01-高斯分布 - 图71$ %0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AZ%3D%5Cbegin%7Bpmatrix%7DX%5C%5CY%5Cend%7Bpmatrix%7D%5Csim%20N%5Cleft%28%0A%5Cbegin%7Bbmatrix%7D%5Cmu%5C%5CA%5Cmu%2Bb%5Cend%7Bbmatrix%7D%2C%0A%5Cbegin%7Bbmatrix%7D%0A%5CLambda%5E%7B-1%7D%26%5CDelta%5C%5C%0A%5CDelta%5ET%26A%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%0A%5Cend%7Bbmatrix%7D%0A%5Cright%29%0A%5Cend%7Baligned%7D%0A)

于是转化为求 $S01-高斯分布 - 图72$ 矩阵

$S01-高斯分布 - 图73$ %5C%5C%0A%26%3DE(%5BX-E(X)%5D%5BY-E(Y)%5D%5ET)%5C%5C%0A%26%3DE%5B(X-%5Cmu)(AX%2Bb%2B%5Cepsilon-A%5Cmu-b)%5ET%5D%5C%5C%0A%26%3DE%5B(X-%5Cmu)(A(X-%5Cmu)%2B%5Cepsilon)%5ET%5D%5C%5C%0A%26%3DE%5B(X-%5Cmu)(X-%5Cmu)%5ETA%5ET%2B(X-%5Cmu)%5Cepsilon%5ET%5D%5C%5C%0A%26%3DE%5B(X-%5Cmu)(X-%5Cmu)%5ETA%5ET%2BE%5B(X-%5Cmu)%5Cepsilon%5ET%5D%5C%5C%0A%26%3DE%5B(X-%5Cmu)(X-%5Cmu)%5ETA%5ET%5D%2BE(X-%5Cmu)E(%5Cepsilon%5ET)%5C%5C%0A%26%3DE%5B(X-%5Cmu)(X-%5Cmu)%5ET%5DA%5ET%5C%5C%0A%26%3D%5CLambda%5E%7B-1%7DA%5ET%5C%5C%0A%5CRightarrow%20Z%26%5Csim%20N%5Cleft(%0A%5Cbegin%7Bbmatrix%7D%5Cmu%5C%5CA%5Cmu%2Bb%5Cend%7Bbmatrix%7D%2C%0A%5Cbegin%7Bbmatrix%7D%0A%5CLambda%5E%7B-1%7D%26%5CLambda%5E%7B-1%7DA%5ET%5C%5C%0AA%5CLambda%5E%7B-1%7D%26A%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%0A%5Cend%7Bbmatrix%7D%5Cright)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5CDelta%26%3DCov%28X%2CY%29%5C%5C%0A%26%3DE%28%5BX-E%28X%29%5D%5BY-E%28Y%29%5D%5ET%29%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28AX%2Bb%2B%5Cepsilon-A%5Cmu-b%29%5ET%5D%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28A%28X-%5Cmu%29%2B%5Cepsilon%29%5ET%5D%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28X-%5Cmu%29%5ETA%5ET%2B%28X-%5Cmu%29%5Cepsilon%5ET%5D%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28X-%5Cmu%29%5ETA%5ET%2BE%5B%28X-%5Cmu%29%5Cepsilon%5ET%5D%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28X-%5Cmu%29%5ETA%5ET%5D%2BE%28X-%5Cmu%29E%28%5Cepsilon%5ET%29%5C%5C%0A%26%3DE%5B%28X-%5Cmu%29%28X-%5Cmu%29%5ET%5DA%5ET%5C%5C%0A%26%3D%5CLambda%5E%7B-1%7DA%5ET%5C%5C%0A%5CRightarrow%20Z%26%5Csim%20N%5Cleft%28%0A%5Cbegin%7Bbmatrix%7D%5Cmu%5C%5CA%5Cmu%2Bb%5Cend%7Bbmatrix%7D%2C%0A%5Cbegin%7Bbmatrix%7D%0A%5CLambda%5E%7B-1%7D%26%5CLambda%5E%7B-1%7DA%5ET%5C%5C%0AA%5CLambda%5E%7B-1%7D%26A%5CLambda%5E%7B-1%7DA%5ET%2BL%5E%7B-1%7D%0A%5Cend%7Bbmatrix%7D%5Cright%29%0A%5Cend%7Baligned%7D%0A)