S04-降维

过拟合

我们知道训练的模型可能出现过拟合的现象，即泛化误差大训练误差小。为了解决过拟合一般有三种方法

1. 增加样本量
2. 正则化
3. 降维

维数灾难

从直觉上讲，我们觉得样本数据的特征(维度)越多，我们训练出来的模型就越准确，但是实际上是不正确的，当维度增加到一定程度，模型效果反而变差，这个现象称为维数灾难。如图

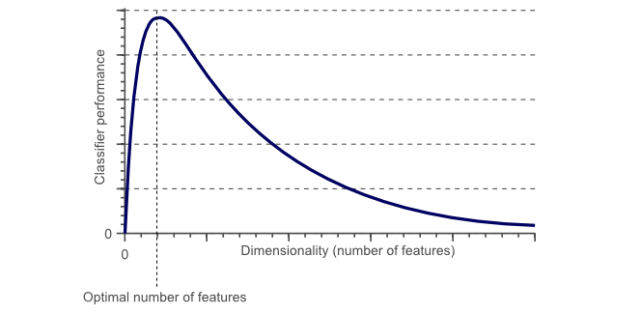
造成这个现象的原因是模型学习到了很多数据集中的噪声和特例，因此对于现实数据往往会效果较差，因为现实数据是没有这些噪声以及异常特性的

数据稀疏性

• 在特征空间为1维时，10个训练实例覆盖在一维轴上，假设轴长为5，那么每个样本平均每个单位有2个样本。特征空间为2维时，我们仍然用10个实例进行训练，此时二维空间的面积是5x5=25，样本密度是10/25=0.4，即每个单位面积有0.4个样本。在特征空间为3维时，10个样本的密度是10/(5x5x5)=0.08，即每个单位体积有0.08个样本。如果我们不断的增加特征，特征维度就会不断变大，于是样本空间变得越来越稀疏。由于稀疏的原因，随着特征维度的不断变大，我们很容易的就找到一个能将样本按类别完美分开的超平面，因为训练样本落到该空间的最优超平面错误一边的概率会随着维度增加无限变小，此时就出现了过拟合现象
• 显然如果要避免出现样本很稀疏的情况，最简单的方式就是增加样本量，但是根据上述分析可以看出，随着维度增加，保持样本密度的样本量是要以指数级增加的，这在现实中十分困难

数据分布的边缘性

• 以二维为例，如图所示，正方形中心代表样本每个维度的中心即均值点，圆为正方形内接圆。假如数据如左图一样，分布在内接圆外，那么显然很难找到正确的切分直线，容易出现过拟合。但是如果样本都分布在内接圆的内部，那么相对来说更容易找到合适的切分直线，不易出现过拟合
  
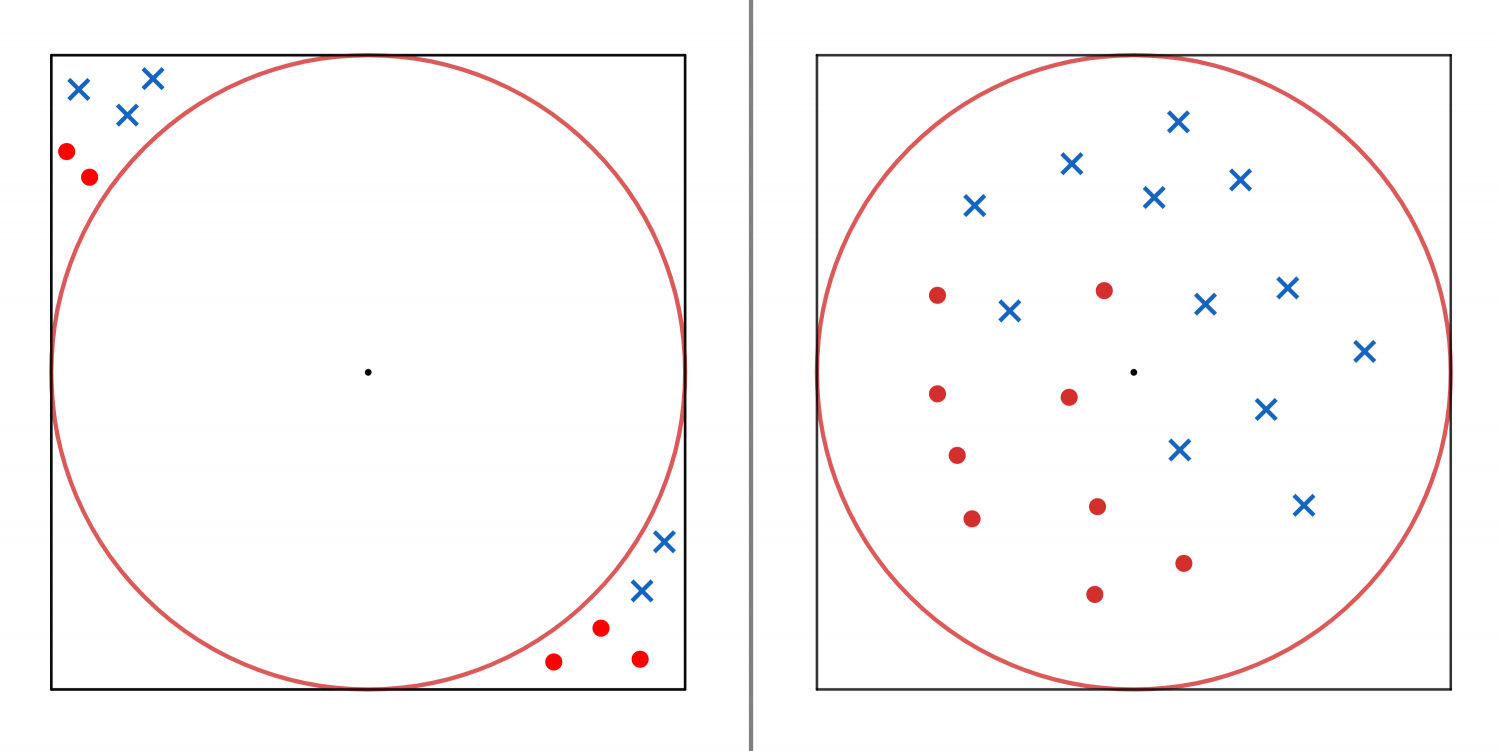
• 不妨设正方形面积为1，计算内接圆的面积占正方形的比例
  

推广到更高维，对于一个n维空间，超立方体的内接超球体占超立方体的体积比例为，那么显然有，即越高维的空间，数据就越分布在超球以外的部分，那么根据之前的分析知道很难找到合适的超平面切分样本。也就是说高维空间里的所有数据都远离其中心，那么样本点到中心点欧氏距离的最大值和最小值趋于接近，等价于下式

从另一个角度来看，高维单元空间可以说是几乎完全由超立方体的“边角”所组成的，没有“中部”。因此，在高维空间用距离来衡量样本相似性的方法已经渐渐失效。所以以距离为标准的分类算法（欧氏距离，曼哈顿距离，马氏距离）在低维空间会有更好的表现，在高维空间就会出现收敛速度非常慢甚至无法使用的情况。类似的，高斯分布在高维空间会变得更加平坦，而且尾巴也会更长

降维

因为维数灾难的存在，我们对于维数过高的样本就要进行降维。降维的方法一般有三类：

1. 直接降维：也叫特征选择，就是将经验上没有用的特征直接剔除
2. 线性降维：PCA(主成分分析),MDS(多维缩放)
3. 非线性降维：流形方法，例如ISOMAP(等度量映射),LLE(局部线性嵌入)