S06P04-隐马尔科夫模型

隐马尔科夫模型(Hidden Markov Model)

对于一般的概率图模型，我们认为各样本之间是独立同分布的，但是也可以认为样本之间不独立，而且是关于一个时间序列隐变量生成的，这样在概率图模型中添加了时间序列的系统称为动态模型(dynamic model)
HMM就是一种动态模型，可以认为样本是由一个隐藏的马尔科夫链生成不可观测的状态随机序列，称为状态序列；再由每个状态生成一个观测，最终生成整个样本的观测序列。可以把序列的每一个位置看作一个时刻，在HMM中的状态随机序列是离散的

定义

先定义一些符号
设#card=math&code=I%3D%28i_1%2Ci_2%2C%5Ccdots%2Ci_T%29)是长度为的状态序列，#card=math&code=O%3D%28o_1%2Co_2%2C%5Ccdots%2Co_T%29)为对应的观测序列
设是每个状态所有取值的集合，是每个观测所有取值的集合
根据上面述定义，可以画出如下概率有向图

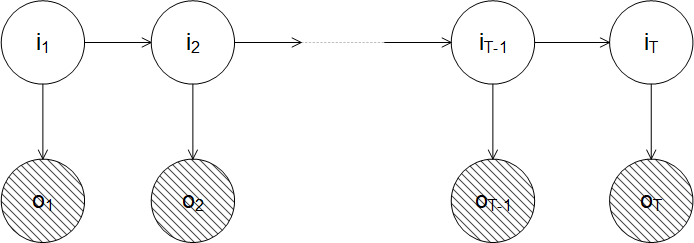HMM由三个参数确定

1. 初始概率分布：对应的是初始状态的概率向量#card=math&code=%5Cpi%3D%28%5Cpi_i%29)，其中%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=%5Cpi_i%3DP%28i_1%3Dq_i%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A)

即时刻时处于状态的概率

1. 状态转移矩阵：，其中%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%3Bj%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=a%7Bij%7D%3DP%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%3Bj%3D1%2C2%2C%5Ccdots%2CN%0A)

即在时刻处于状态，而在时刻转移到状态的概率

1. 观测概率矩阵，又叫发射矩阵：%5D%7BN%5Ctimes%20M%7D#card=math&code=B%3D%5Bb_j%28k%29%5D%7BN%5Ctimes%20M%7D)，其中%3DP(o_t%3Dv_k%7Ci_t%3Dq_j)%2C%5Cquad%20k%3D1%2C2%2C%5Ccdots%2CM%3Bj%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=b_j%28k%29%3DP%28o_t%3Dv_k%7Ci_t%3Dq_j%29%2C%5Cquad%20k%3D1%2C2%2C%5Ccdots%2CM%3Bj%3D1%2C2%2C%5Ccdots%2CN%0A)

即在时刻处于状态的条件下生成的概率

根据这三个参数，就可以确定HMM，称为HMM的三要素，统一写为

%0A#card=math&code=%5Clambda%3D%28%5Cpi%2CA%2CB%29%0A)

根据以上的定义，可以发现HMM基于以下两点基本假设

1. 齐次马尔科夫性假设：假设隐藏的马尔科夫链在任意时刻的状态只与前一时刻的状态相关，而与其他时刻的状态和观测无关，也与时刻无关%3DP(it%7Ci%7Bt-1%7D)%2C%5Cquad%20t%3D1%2C2%2C%5Ccdots%2CT%0A#card=math&code=P%28i%7Bt%7D%7Ci%7Bt-1%7D%2C%5Ccdots%2Ci1%2Co%7Bt-1%7D%2C%5Ccdots%2Co1%29%3DP%28i_t%7Ci%7Bt-1%7D%29%2C%5Cquad%20t%3D1%2C2%2C%5Ccdots%2CT%0A)

1. 观测独立性假设：假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，而与其他观测及状态无关%3DP(ot%7Ci_t)%2C%5Cquad%20t%3D1%2C2%2C%5Ccdots%2CT%0A#card=math&code=P%28o_t%7Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%2Co_1%2C%5Ccdots%2Co%7Bt-1%7D%2Co_%7Bt%2B1%7D%2C%5Ccdots%2Co_T%29%3DP%28o_t%7Ci_t%29%2C%5Cquad%20t%3D1%2C2%2C%5Ccdots%2CT%0A)

HMM包含了三个基本问题

1. 概率计算问题。关于参数和观测序列，计算#card=math&code=P%28O%7C%5Clambda%29)
2. 学习问题。已知观测序列，估计参数
3. 预测问题，又称为解码(decoding)问题。已知参数和观测序列，求对应最有可能的状态序列，即使#card=math&code=P%28I%7CO%2C%5Clambda%29)最大的状态序列

概率计算问题

%26%3D%5Csum_IP(O%2CI%7C%5Clambda)%5C%5C%0A%26%3D%5Csum_IP(O%7CI%2C%5Clambda)P(I%7C%5Clambda)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28O%7C%5Clambda%29%26%3D%5Csum_IP%28O%2CI%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum_IP%28O%7CI%2C%5Clambda%29P%28I%7C%5Clambda%29%0A%5Cend%7Baligned%7D%0A)

计算#card=math&code=P%28I%7C%5Clambda%29)，利用齐次马尔科夫性假设

%26%3DP(i1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda)%5C%5C%0A%26%3DP(i_T%7Ci%7BT-1%7D%2C%5Ccdots%2Ci1%2C%5Clambda)P(i%7BT-1%7D%2C%5Ccdots%2Ci1%7C%5Clambda)%5C%5C%0A%26%3DP(i_T%7Ci%7BT-1%7D%2C%5Clambda)P(i%7BT-1%7D%2C%5Ccdots%2Ci_1%7C%5Clambda)%5C%5C%0A%26%3D%5Ccdots%5C%5C%0A%26%3DP(i_T%7Ci%7BT-1%7D%2C%5Clambda)P(i%7BT-1%7D%7Ci%7BT-2%7D%2C%5Clambda)%5Ccdots%20P(i2%7Ci_1%2C%5Clambda)P(i_1%2C%5Clambda)%5C%5C%0A%26%3Da%7Bi%7BT-1%7Di_T%7Da%7Bi%7BT-2%7Di%7BT-1%7D%7D%5Ccdots%20a%7Bi_2i_1%7D%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Dit%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28I%7C%5Clambda%29%26%3DP%28i_1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda%29%5C%5C%0A%26%3DP%28i_T%7Ci%7BT-1%7D%2C%5Ccdots%2Ci1%2C%5Clambda%29P%28i%7BT-1%7D%2C%5Ccdots%2Ci1%7C%5Clambda%29%5C%5C%0A%26%3DP%28i_T%7Ci%7BT-1%7D%2C%5Clambda%29P%28i%7BT-1%7D%2C%5Ccdots%2Ci_1%7C%5Clambda%29%5C%5C%0A%26%3D%5Ccdots%5C%5C%0A%26%3DP%28i_T%7Ci%7BT-1%7D%2C%5Clambda%29P%28i%7BT-1%7D%7Ci%7BT-2%7D%2C%5Clambda%29%5Ccdots%20P%28i2%7Ci_1%2C%5Clambda%29P%28i_1%2C%5Clambda%29%5C%5C%0A%26%3Da%7Bi%7BT-1%7Di_T%7Da%7Bi%7BT-2%7Di%7BT-1%7D%7D%5Ccdots%20a%7Bi_2i_1%7D%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Di_t%7D%0A%5Cend%7Baligned%7D%0A)

计算#card=math&code=P%28O%7CI%2C%5Clambda%29)，利用观测独立性假设

%26%3DP(o1%2C%5Ccdots%2Co_T%7Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda)%5C%5C%0A%26%3DP(o_T%7Co_1%2C%5Ccdots%2Co%7BT-1%7D%2Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda)P(o_1%2C%5Ccdots%2Co%7BT-1%7D%7Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda)%5C%5C%0A%26%3DP(o_T%7Ci_T%2C%5Clambda)P(o_1%2C%5Ccdots%2Co%7BT-1%7D%7Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda)%5C%5C%0A%26%3D%5Ccdots%5C%5C%0A%26%3DP(o_T%7Ci_T%2C%5Clambda)P(o%7BT-1%7D%7Ci%7BT-1%7D%2C%5Clambda)%5Ccdots%20P(o_1%7Ci_1%2C%5Clambda)%5C%5C%0A%26%3Db%7BiT%7D(o_T)b%7Bi%7BT-1%7D%7D(o%7BT-1%7D)%5Ccdots%20b%7Bi_1%7D(o_1)%5C%5C%0A%26%3D%5Cprod%7Bt%3D1%7D%5ETb%7Bi_t%7D(o_t)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28O%7CI%2C%5Clambda%29%26%3DP%28o_1%2C%5Ccdots%2Co_T%7Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda%29%5C%5C%0A%26%3DP%28o_T%7Co_1%2C%5Ccdots%2Co%7BT-1%7D%2Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda%29P%28o_1%2C%5Ccdots%2Co%7BT-1%7D%7Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda%29%5C%5C%0A%26%3DP%28o_T%7Ci_T%2C%5Clambda%29P%28o_1%2C%5Ccdots%2Co%7BT-1%7D%7Ci1%2Ci_2%2C%5Ccdots%2Ci_T%2C%5Clambda%29%5C%5C%0A%26%3D%5Ccdots%5C%5C%0A%26%3DP%28o_T%7Ci_T%2C%5Clambda%29P%28o%7BT-1%7D%7Ci%7BT-1%7D%2C%5Clambda%29%5Ccdots%20P%28o_1%7Ci_1%2C%5Clambda%29%5C%5C%0A%26%3Db%7BiT%7D%28o_T%29b%7Bi%7BT-1%7D%7D%28o%7BT-1%7D%29%5Ccdots%20b%7Bi_1%7D%28o_1%29%5C%5C%0A%26%3D%5Cprod%7Bt%3D1%7D%5ETb_%7Bi_t%7D%28o_t%29%0A%5Cend%7Baligned%7D%0A)

代入即得

%3D%5CsumI%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Dit%7D%5Cprod%7Bt%3D1%7D%5ETb%7Bi_t%7D(o_t)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28O%7C%5Clambda%29%3D%5Csum_I%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Dit%7D%5Cprod%7Bt%3D1%7D%5ETb_%7Bi_t%7D%28o_t%29%0A%5Cend%7Baligned%7D%0A)

这样可以算出来，但是可以发现，当时刻越大，状态取值越多，计算复杂度为#card=math&code=O%28TN%5ET%29)，这种直接计算的方法计算难度是非常大的，因此有了简化计算的其他算法

前向算法

定义图中虚框内的联合概率，即时刻之前的观测序列为及时刻的状态为的概率

%26%3DP(o1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(o1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%2Ci%7Bt-1%7D%3Dqj%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(ot%7Co_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Cit%3Dq_i%2Ci%7Bt-1%7D%3Dqj%2C%5Clambda)P(o_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Cit%3Dq_i%2Ci%7Bt-1%7D%3Dqj%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(ot%7Ci_t%3Dq_i%2C%5Clambda)P(i_t%3Dq_i%7Co_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Ci%7Bt-1%7D%3Dq_j%2C%5Clambda)P(o_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Ci%7Bt-1%7D%3Dq_j%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(ot%7Ci_t%3Dq_i%2C%5Clambda)P(i_t%3Dq_i%7Ci%7Bt-1%7D%3Dqj%2C%5Clambda)%5Calpha%7Bt-1%7D(j)%5C%5C%0A%26%3DP(ot%7Ci_t%3Dq_i%2C%5Clambda)%5Csum%7Bj%3D1%7D%5ENP(it%3Dq_i%7Ci%7Bt-1%7D%3Dqj%2C%5Clambda)%5Calpha%7Bt-1%7D(j)%5C%5C%0A%26%3Dbi(o_t)%5Csum%7Bj%3D1%7D%5EN%5Calpha%7Bt-1%7D(j)a%7Bji%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Calphat%28i%29%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28o1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%2Ci%7Bt-1%7D%3Dqj%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28ot%7Co_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Cit%3Dq_i%2Ci%7Bt-1%7D%3Dqj%2C%5Clambda%29P%28o_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Cit%3Dq_i%2Ci%7Bt-1%7D%3Dqj%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28ot%7Ci_t%3Dq_i%2C%5Clambda%29P%28i_t%3Dq_i%7Co_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Ci%7Bt-1%7D%3Dq_j%2C%5Clambda%29P%28o_1%2Co_2%2C%5Ccdots%2Co%7Bt-1%7D%2Ci%7Bt-1%7D%3Dq_j%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28ot%7Ci_t%3Dq_i%2C%5Clambda%29P%28i_t%3Dq_i%7Ci%7Bt-1%7D%3Dqj%2C%5Clambda%29%5Calpha%7Bt-1%7D%28j%29%5C%5C%0A%26%3DP%28ot%7Ci_t%3Dq_i%2C%5Clambda%29%5Csum%7Bj%3D1%7D%5ENP%28it%3Dq_i%7Ci%7Bt-1%7D%3Dqj%2C%5Clambda%29%5Calpha%7Bt-1%7D%28j%29%5C%5C%0A%26%3Dbi%28o_t%29%5Csum%7Bj%3D1%7D%5EN%5Calpha%7Bt-1%7D%28j%29a%7Bji%7D%0A%5Cend%7Baligned%7D%0A)

由此式可看出#card=math&code=%5Calpha_t%28i%29)关于时刻的递归关系，又因为

%3D%5Csum%7Bi%3D1%7D%5ENP(o_1%2Co_2%2C%5Ccdots%2Co_T%2Ci_T%3Dq_i%7C%5Clambda)%3D%5Csum%7Bi%3D1%7D%5EN%5CalphaT(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5ENP%28o1%2Co_2%2C%5Ccdots%2Co_T%2Ci_T%3Dq_i%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%5Calpha_T%28i%29%0A)

于是通过递归可以计算出#card=math&code=P%28O%7C%5Clambda%29)，这里#card=math&code=%5Calpha_t%28i%29)又称为前向概率，这种计算#card=math&code=P%28O%7C%5Clambda%29)的方法称为观测序列概率的前向算法。下面总结前向算法流程

(1)计算初值

%26%3DP(o_1%2Ci_1%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3DP(o_1%7Ci_1%3Dq_i%2C%5Clambda)P(i_1%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3D%5Cpi_ib_i(o_1)%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%20%0A%5Calpha_1%28i%29%26%3DP%28o_1%2Ci_1%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3DP%28o_1%7Ci_1%3Dq_i%2C%5Clambda%29P%28i_1%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3D%5Cpi_ib_i%28o_1%29%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Baligned%7D%0A)

(2)对递推计算

%3Dbi(o%7Bt%2B1%7D)%5Csum%7Bj%3D1%7D%5EN%5Calpha_t(j)a%7Bji%7D%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=%5Calpha%7Bt%2B1%7D%28i%29%3Db_i%28o%7Bt%2B1%7D%29%5Csum%7Bj%3D1%7D%5EN%5Calpha_t%28j%29a%7Bji%7D%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A)

(3)计算终值

%3D%5Csum%7Bi%3D1%7D%5EN%5Calpha_T(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%5Calpha_T%28i%29%0A)

显然这个算法的计算法复杂度为#card=math&code=O%28N%5E2T%29)，比直接计算更简便更高效

后向算法

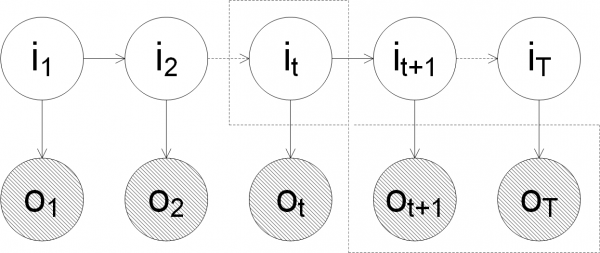定义图中虚框内的条件概率，即时刻之后的观测序列为在时刻的状态为条件下的概率

%26%3DP(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2Ci_t%3Dq_i%2C%5Clambda)P(i%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP(o%7Bt%2B1%7D%7Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%2Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda)P(o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP(o%7Bt%2B1%7D%7Ci%7Bt%2B1%7D%3Dq_j%2C%5Clambda)%5Cbeta%7Bt%2B1%7D(j)%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7Dbj(o%7Bt%2B1%7D)%5Cbeta%7Bt%2B1%7D(j)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cbeta_t%28i%29%26%3DP%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENP%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2Ci_t%3Dq_i%2C%5Clambda%29P%28i%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP%28o%7Bt%2B1%7D%7Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%2Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda%29P%28o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7DP%28o%7Bt%2B1%7D%7Ci%7Bt%2B1%7D%3Dq_j%2C%5Clambda%29%5Cbeta%7Bt%2B1%7D%28j%29%5C%5C%0A%26%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7Dbj%28o%7Bt%2B1%7D%29%5Cbeta_%7Bt%2B1%7D%28j%29%0A%5Cend%7Baligned%7D%0A)

由此式可看出#card=math&code=%5Cbeta_t%28i%29)关于时刻的递归关系，又因为

%26%3D%5Csum%7Bi%3D1%7D%5ENP(o_1%2Co_2%2C%5Ccdots%2Co_T%2Ci_1%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5ENP(o1%2Co_2%2C%5Ccdots%2Co_T%7Ci_1%3Dq_i%2C%5Clambda)P(i_1%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CpiiP(o_1%7Co_2%2C%5Ccdots%2Co_T%2Ci_1%3Dq_i%2C%5Clambda)P(o_2%2C%5Ccdots%2Co_T%7Ci_1%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CpiiP(o_1%7Ci_1%3Dq_i%2C%5Clambda)%5Cbeta_1(i)%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cpiib_i(o_1)%5Cbeta_1(i)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28O%7C%5Clambda%29%26%3D%5Csum%7Bi%3D1%7D%5ENP%28o1%2Co_2%2C%5Ccdots%2Co_T%2Ci_1%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5ENP%28o1%2Co_2%2C%5Ccdots%2Co_T%7Ci_1%3Dq_i%2C%5Clambda%29P%28i_1%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CpiiP%28o_1%7Co_2%2C%5Ccdots%2Co_T%2Ci_1%3Dq_i%2C%5Clambda%29P%28o_2%2C%5Ccdots%2Co_T%7Ci_1%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5CpiiP%28o_1%7Ci_1%3Dq_i%2C%5Clambda%29%5Cbeta_1%28i%29%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cpi_ib_i%28o_1%29%5Cbeta_1%28i%29%0A%5Cend%7Baligned%7D%0A)

于是通过递归可以计算出#card=math&code=P%28O%7C%5Clambda%29)，这里#card=math&code=%5Cbeta_t%28i%29)又称为后向概率，这种计算#card=math&code=P%28O%7C%5Clambda%29)的方法称为观测序列概率的后向算法。下面总结后向算法流程

(1)规定初值
根据定义，#card=math&code=%5CbetaT%28i%29)应该为时刻之后的观测序列为在时刻的状态为条件下的概率，而实际上时刻之后的观测序列是未知的，那么取中任何值都可能，因此将其概率规定为1

%3D1%0A#card=math&code=%5Cbeta_T%28i%29%3D1%0A)

(2)对递推计算

%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7Dbj(o%7Bt%2B1%7D)%5Cbeta%7Bt%2B1%7D(j)%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=%5Cbeta%7Bt%7D%28i%29%3D%5Csum%7Bj%3D1%7D%5ENa%7Bij%7Dbj%28o%7Bt%2B1%7D%29%5Cbeta_%7Bt%2B1%7D%28j%29%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A)

(3)计算终值

%3D%5Csum%7Bi%3D1%7D%5EN%5Cpi_ib_i(o_1)%5Cbeta_1(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%5Cpi_ib_i%28o_1%29%5Cbeta_1%28i%29%0A)

相关概率值的计算

%5Cbetat(i)%26%3DP(o_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda)P(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3DP(o_1%2Co_2%2C%5Ccdots%2Co_t%7Ci_t%3Dq_i%2C%5Clambda)P(i_t%3Dq_i%7C%5Clambda)P(o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3DP(o_1%2Co_2%2C%5Ccdots%2Co_t%2Co%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda)P(i_t%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3DP(o_1%2Co_2%2C%5Ccdots%2Co_T%2Ci_t%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3DP(O%2Ci_t%3Dq_i%7C%5Clambda)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Calpha_t%28i%29%5Cbeta_t%28i%29%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda%29P%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_t%7Ci_t%3Dq_i%2C%5Clambda%29P%28i_t%3Dq_i%7C%5Clambda%29P%28o%7Bt%2B1%7D%2Co%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_t%2Co%7Bt%2B1%7D%2Co_%7Bt%2B2%7D%2C%5Ccdots%2Co_T%7Ci_t%3Dq_i%2C%5Clambda%29P%28i_t%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_T%2Ci_t%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3DP%28O%2Ci_t%3Dq_i%7C%5Clambda%29%0A%5Cend%7Baligned%7D%0A)

即给定模型条件下，时刻状态为且观测序列为的概率为

%3D%5Calpha_t(i)%5Cbeta_t(i)%0A#card=math&code=P%28O%2Ci_t%3Dq_i%7C%5Clambda%29%3D%5Calpha_t%28i%29%5Cbeta_t%28i%29%0A)

因此可得

%3D%5Csum%7Bi%3D1%7D%5ENP(O%2Ci_t%3Dq_i%7C%5Clambda)%3D%5Csum%7Bi%3D1%7D%5EN%5Calphat(i)%5Cbeta_t(i)%0A#card=math&code=P%28O%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5ENP%28O%2Cit%3Dq_i%7C%5Clambda%29%3D%5Csum%7Bi%3D1%7D%5EN%5Calpha_t%28i%29%5Cbeta_t%28i%29%0A)

下面计算模型参数为下，观测序列为且的概率

%26%3DP(o1%2Co_2%2C%5Ccdots%2Co_T%2Ci_t%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda)%5C%5C%0A%26%3DP(o%7Bt%2B1%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Co_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%2C%5Clambda)P(o_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)P(o%7Bt%2B1%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)P(o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Co%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%2Ci_t%3Dq_i%2C%5Clambda)P(o%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)P(o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda)P(o%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)%5Cbeta%7Bt%2B1%7D(j)P(o%7Bt%2B1%7D%7Ci_t%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda)P(i%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)a%7Bij%7D%5Cbeta%7Bt%2B1%7D(j)P(o%7Bt%2B1%7D%7Ci%7Bt%2B1%7D%3Dq_j%2C%5Clambda)%5C%5C%0A%26%3D%5Calpha_t(i)a%7Bij%7Dbj(o%7Bt%2B1%7D)%5Cbeta%7Bt%2B1%7D(j)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28O%2Ci_t%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%29%26%3DP%28o_1%2Co_2%2C%5Ccdots%2Co_T%2Ci_t%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%29%5C%5C%0A%26%3DP%28o%7Bt%2B1%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Co_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%2C%5Clambda%29P%28o_1%2Co_2%2C%5Ccdots%2Co_t%2Ci_t%3Dq_i%7C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29P%28o%7Bt%2B1%7D%2C%5Ccdots%2CoT%2Ci%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29P%28o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Co%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%2Ci_t%3Dq_i%2C%5Clambda%29P%28o%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29P%28o%7Bt%2B2%7D%2C%5Ccdots%2CoT%7Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda%29P%28o%7Bt%2B1%7D%2Ci%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29%5Cbeta%7Bt%2B1%7D%28j%29P%28o%7Bt%2B1%7D%7Ci_t%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%2C%5Clambda%29P%28i%7Bt%2B1%7D%3Dqj%7Ci_t%3Dq_i%2C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29a%7Bij%7D%5Cbeta%7Bt%2B1%7D%28j%29P%28o%7Bt%2B1%7D%7Ci%7Bt%2B1%7D%3Dq_j%2C%5Clambda%29%5C%5C%0A%26%3D%5Calpha_t%28i%29a%7Bij%7Dbj%28o%7Bt%2B1%7D%29%5Cbeta_%7Bt%2B1%7D%28j%29%0A%5Cend%7Baligned%7D%0A)

学习问题

学习问题其实就是参数的估计，由概率计算问题已经计算出了#card=math&code=P%28O%7C%5Clambda%29)，于是运用极大似然估计来计算参数。因为HMM中含有隐变量，因此采用EM算法来求解这个极大似然估计问题

%7D%26%3D%5Carg%5Cmax%5Clambda%5Csum_IP(I%7CO%2C%5Clambda%5E%7B(s)%7D)%5Clog%20P(O%2CI%7C%5Clambda)%20%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5CsumI%5Cfrac%7BP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%7D%7BP(O%7C%5Clambda%5E%7B(s)%7D)%7D%5Clog%20P(O%2CI%7C%5Clambda)%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5Cfrac%7B1%7D%7BP(O%7C%5Clambda%5E%7B(s)%7D)%7D%5CsumIP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(O%2CI%7C%5Clambda)%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5CsumIP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(O%2CI%7C%5Clambda)%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Clambda%5E%7B%28s%2B1%29%7D%26%3D%5Carg%5Cmax%5Clambda%5CsumIP%28I%7CO%2C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28O%2CI%7C%5Clambda%29%20%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5CsumI%5Cfrac%7BP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7BP%28O%7C%5Clambda%5E%7B%28s%29%7D%29%7D%5Clog%20P%28O%2CI%7C%5Clambda%29%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5Cfrac%7B1%7D%7BP%28O%7C%5Clambda%5E%7B%28s%29%7D%29%7D%5CsumIP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28O%2CI%7C%5Clambda%29%5C%5C%0A%26%3D%5Carg%5Cmax%5Clambda%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28O%2CI%7C%5Clambda%29%5C%5C%0A%5Cend%7Baligned%7D%0A)

令%7D)%3D%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(O%2CI%7C%5Clambda)#card=math&code=Q%28%5Clambda%2C%5Clambda%5E%7B%28s%29%7D%29%3D%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28O%2CI%7C%5Clambda%29)，将直接计算法得到的#card=math&code=P%28O%2CI%7C%5Clambda%29)代入

%7D)%26%3D%5CsumIP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Dit%7D%5Cprod%7Bt%3D1%7D%5ETb%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Cleft%5B%5Clog%5Cpi%7Bi1%7D%2B%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20a%7Bi_ti%7Bt%2B1%7D%7D%2B%5Csum%7Bt%3D1%7D%5ET%5Clog%20b%7Bit%7D(o_t)%5Cright%5D%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AQ%28%5Clambda%2C%5Clambda%5E%7B%28s%29%7D%29%26%3D%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%5Cpi%7Bi1%7D%5Cprod%7Bt%3D2%7D%5ETa%7Bi%7Bt-1%7Dit%7D%5Cprod%7Bt%3D1%7D%5ETb%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Cleft%5B%5Clog%5Cpi%7Bi1%7D%2B%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20a%7Bi_ti%7Bt%2B1%7D%7D%2B%5Csum%7Bt%3D1%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5Cright%5D%5C%5C%0A%5Cend%7Baligned%7D%0A)

1. 求%7D#card=math&code=%5Cpi%5E%7B%28s%2B1%29%7D)%7D%26%3D%5Carg%5Cmax%5Cpi%20Q(%5Clambda%2C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5CsumIP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Ccdots%5Csum%7BiT%7DP(i_1%2Ci_2%2C%5Ccdots%2Ci_T%2CO%7C%5Clambda%5E%7B(s)%7D)%5Clog%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Clog%5Cpi%7Bi1%7D%5Csum%7Bi2%7D%5Ccdots%5Csum%7BiT%7DP(i_1%2Ci_2%2C%5Ccdots%2Ci_T%2CO%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Clog%5Cpi%7Bi1%7DP(i_1%2CO%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cpi%7Bi%7DP(i1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cpi%5E%7B%28s%2B1%29%7D%26%3D%5Carg%5Cmax%5Cpi%20Q%28%5Clambda%2C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Ccdots%5Csum%7BiT%7DP%28i_1%2Ci_2%2C%5Ccdots%2Ci_T%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%5Cpi%7Bi1%7D%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Clog%5Cpi%7Bi1%7D%5Csum%7Bi2%7D%5Ccdots%5Csum%7BiT%7DP%28i_1%2Ci_2%2C%5Ccdots%2Ci_T%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi_1%7D%5Clog%5Cpi%7Bi1%7DP%28i_1%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax%5Cpi%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cpi%7Bi%7DP%28i1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%0A%5Cend%7Baligned%7D%0A)
   %7D)%5C%5C%0As.t.%5Cquad%5Csum%7Bi%3D1%7D%5EN%5Cpii%3D1%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cmax%5Cpi%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cpi%7Bi%7DP%28i1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0As.t.%5Cquad%5Csum%7Bi%3D1%7D%5EN%5Cpii%3D1%0A%5Cend%7Bgathered%7D%0A)
   %3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cpi%7Bi%7DP(i_1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%2B%5Ceta(1-%5Csum%7Bi%3D1%7D%5EN%5Cpii)%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%5Cpi_i%7D%3D%5Cfrac%7BP(i_1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%7D%7B%5Cpi%7Bi%7D%7D-%5Ceta%3D0%5C%5C%0A%26%5CRightarrow%5Ceta%5Cpi%7Bi%7D%3DP(i_1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%5CRightarrow%5Csum%7Bi%3D1%7D%5EN%5Ceta%5Cpi%7Bi%7D%3D%5Csum%7Bi%3D1%7D%5ENP(i1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%5CRightarrow%5Ceta%3DP(O%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%5CRightarrow%5Cpi%7Bi%7D%5E%7B(s%2B1)%7D%3D%5Cfrac%7BP(i1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%7D%7BP(O%7C%5Clambda%5E%7B(s)%7D)%7D%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%5Cpi%5E%7B(s%2B1)%7D%3D(%5Cpi_1%5E%7B(s%2B1)%7D%2C%5Cpi_2%5E%7B(s%2B1)%7D%2C%5Ccdots%2C%5Cpi_N%5E%7B(s%2B1)%7D)%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AL%28%5Cpi%2C%5Ceta%29%3D%5Csum%7Bi%3D1%7D%5EN%5Clog%5Cpi%7Bi%7DP%28i_1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Ceta%281-%5Csum%7Bi%3D1%7D%5EN%5Cpii%29%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%5Cpi_i%7D%3D%5Cfrac%7BP%28i_1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7B%5Cpi%7Bi%7D%7D-%5Ceta%3D0%5C%5C%0A%26%5CRightarrow%5Ceta%5Cpi%7Bi%7D%3DP%28i_1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%5CRightarrow%5Csum%7Bi%3D1%7D%5EN%5Ceta%5Cpi%7Bi%7D%3D%5Csum%7Bi%3D1%7D%5ENP%28i1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%5CRightarrow%5Ceta%3DP%28O%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%5CRightarrow%5Cpi%7Bi%7D%5E%7B%28s%2B1%29%7D%3D%5Cfrac%7BP%28i_1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7BP%28O%7C%5Clambda%5E%7B%28s%29%7D%29%7D%0A%5Cend%7Baligned%7D%5C%5C%0A%5C%5C%0A%5Cpi%5E%7B%28s%2B1%29%7D%3D%28%5Cpi_1%5E%7B%28s%2B1%29%7D%2C%5Cpi_2%5E%7B%28s%2B1%29%7D%2C%5Ccdots%2C%5Cpi_N%5E%7B%28s%2B1%29%7D%29%0A%5Cend%7Bgathered%7D%0A)

1. 求%7D#card=math&code=A%5E%7B%28s%2B1%29%7D)%7D%26%3D%5Carg%5CmaxAQ(%5Clambda%2C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20a%7Bi_ti%7Bt%2B1%7D%7D%5C%5C%0A%26%3D%5Carg%5CmaxA%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(i_2%7Ci_1)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Ccdots%5Csum%7BiT%7DP(O%2Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(i_2%7Ci_1)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Csum%7Bi2%7D%5Clog%20P(i_2%7Ci_1)%5Csum%7Bi3%7D%5Ccdots%5Csum%7BiT%7DP(O%2Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B(s)%7D)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Csum%7Bi2%7D%5Clog%20P(i_2%7Ci_1)P(O%2Ci_1%2Ci_2%7C%5Clambda%5E%7B(s)%7D)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP(O%2Ci1%3Dq_i%2Ci_2%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P(i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP(O%2Ci1%3Dq_i%2Ci_2%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%2B%5Ccdots%2B%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP(O%2Ci%7BT-1%7D%3Dq_i%2Ci_T%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AA%5E%7B%28s%2B1%29%7D%26%3D%5Carg%5Cmax_AQ%28%5Clambda%2C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20a%7Bi_ti%7Bt%2B1%7D%7D%5C%5C%0A%26%3D%5Carg%5CmaxA%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28i_2%7Ci_1%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Ccdots%5Csum%7BiT%7DP%28O%2Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28i_2%7Ci_1%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Csum%7Bi2%7D%5Clog%20P%28i_2%7Ci_1%29%5Csum%7Bi3%7D%5Ccdots%5Csum%7BiT%7DP%28O%2Ci_1%2Ci_2%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi1%7D%5Csum%7Bi2%7D%5Clog%20P%28i_2%7Ci_1%29P%28O%2Ci_1%2Ci_2%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci1%3Dq_i%2Ci_2%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5E%7BT-1%7D%5Clog%20P%28i%7Bt%2B1%7D%3Dq_j%7Ci_t%3Dq_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci1%3Dq_i%2Ci_2%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Ccdots%2B%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci%7BT-1%7D%3Dq_i%2Ci_T%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax_A%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%0A%5Cend%7Baligned%7D%0A)

由定义知矩阵是一个概率分布的矩阵，其每一行的和为1，因此最终转化为如下优化问题%7D)%5C%5C%0As.t.%5Cquad%5Csum%7Bj%3D1%7D%5ENa%7Bij%7D%3D1%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5CmaxA%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0As.t.%5Cquad%5Csum%7Bj%3D1%7D%5ENa%7Bij%7D%3D1%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A)
%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%2B%5Csum%7Bi%3D1%7D%5EN%5Cetai(1-%5Csum%7Bj%3D1%7D%5ENa%7Bij%7D)%0A#card=math&code=L%28A%2C%5Ceta%29%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3D1%7D%5EN%5Clog%20a%7Bij%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Csum%7Bi%3D1%7D%5EN%5Cetai%281-%5Csum%7Bj%3D1%7D%5ENa_%7Bij%7D%29%0A)

对矩阵的每一个元素求偏导%7D)-%5Cetai%3D0%5C%5C%0A%5Cbegin%7Baligned%7D%0A%5CRightarrow%26%20a%7Bij%7D%3D%5Cfrac%7B1%7D%7B%5Cetai%7D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Ci%7Bt%7D%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%5CRightarrow%26%5Csum%7Bj%3D1%7D%5ENa%7Bij%7D%3D%5Csum%7Bj%3D1%7D%5EN%5Cfrac%7B1%7D%7B%5Cetai%7D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Ci%7Bt%7D%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%5CRightarrow%5Ceta_i%26%3D%5Csum%7Bj%3D1%7D%5EN%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bj%3D1%7D%5ENP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Cit%3Dq_i%7C%5Clambda%5E%7B(s)%7D)%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20a%7Bij%7D%7D%3D%5Cfrac%7B1%7D%7Ba%7Bij%7D%7D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29-%5Ceta_i%3D0%5C%5C%0A%5Cbegin%7Baligned%7D%0A%5CRightarrow%26%20a%7Bij%7D%3D%5Cfrac%7B1%7D%7B%5Cetai%7D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%5CRightarrow%26%5Csum%7Bj%3D1%7D%5ENa%7Bij%7D%3D%5Csum%7Bj%3D1%7D%5EN%5Cfrac%7B1%7D%7B%5Cetai%7D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dq_i%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%5CRightarrow%5Ceta_i%26%3D%5Csum%7Bj%3D1%7D%5EN%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7D%5Csum%7Bj%3D1%7D%5ENP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Cit%3Dq_i%7C%5Clambda%5E%7B%28s%29%7D%29%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A)
%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Cit%3Dq_i%7C%5Clambda%5E%7B(s)%7D)%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0Aa%7Bij%7D%5E%7B%28s%2B1%29%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci_t%3Dq_i%7C%5Clambda%5E%7B%28s%29%7D%29%7D%0A%5Cend%7Bgathered%7D%0A)

1. 求%7D#card=math&code=B%5E%7B%28s%2B1%29%7D)%7D%26%3D%5Carg%5CmaxBQ(%5Clambda%2C%5Clambda%5E%7B(s)%7D)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D1%7D%5ET%5Clog%20b%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Clog%20b%7Bi1%7D(o_1)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7D%5Ccdots%5Csum%7BiT%7DP(O%2Ci_1%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(o_1%3Dv_k%7Ci_1%3Dq_j)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7D%5Clog%20P(o_1%3Dv_k%7Ci_1%3Dq_j)%5Csum%7Bi2%7D%5Ccdots%5Csum%7BiT%7DP(O%2Ci_1%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B(s)%7D)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7DP(O%2Ci_1%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(o_1%3Dv_k%7Ci_1%3Dq_j)%2B%5Csum_IP(O%2CI%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D(o_t)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7DP(O%2Ci_1%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(o_1%3Dv_k%7Ci_1%3Dq_j)%2B%5Ccdots%2B%5Csum%7BiT%7DP(O%2Ci_T%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(o_T%3Dv_k%7Ci_T%3Dq_j)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bi_t%7DP(O%2Ci_t%7C%5Clambda%5E%7B(s)%7D)%5Clog%20P(o_t%3Dv_k%7Ci_t%3Dq_j)%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bj%3D1%7D%5ENP(O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%5Clog%20b_j(o_t)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AB%5E%7B%28s%2B1%29%7D%26%3D%5Carg%5Cmax_BQ%28%5Clambda%2C%5Clambda%5E%7B%28s%29%7D%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D1%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20b%7Bi1%7D%28o_1%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7D%5Ccdots%5Csum%7BiT%7DP%28O%2Ci_1%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28o_1%3Dv_k%7Ci_1%3Dq_j%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7D%5Clog%20P%28o_1%3Dv_k%7Ci_1%3Dq_j%29%5Csum%7Bi2%7D%5Ccdots%5Csum%7BiT%7DP%28O%2Ci_1%2C%5Ccdots%2Ci_T%7C%5Clambda%5E%7B%28s%29%7D%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7DP%28O%2Ci_1%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28o_1%3Dv_k%7Ci_1%3Dq_j%29%2B%5Csum_IP%28O%2CI%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bt%3D2%7D%5ET%5Clog%20b%7Bi_t%7D%28o_t%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bi1%7DP%28O%2Ci_1%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28o_1%3Dv_k%7Ci_1%3Dq_j%29%2B%5Ccdots%2B%5Csum%7BiT%7DP%28O%2Ci_T%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28o_T%3Dv_k%7Ci_T%3Dq_j%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bi_t%7DP%28O%2Ci_t%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20P%28o_t%3Dv_k%7Ci_t%3Dq_j%29%5C%5C%0A%26%3D%5Carg%5Cmax_B%5Csum%7Bt%3D1%7D%5ET%5Csum_%7Bj%3D1%7D%5ENP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20b_j%28o_t%29%0A%5Cend%7Baligned%7D%0A)

根据定义矩阵是概率矩阵，满足每行的和为1，于是转化为如下优化问题%7D)%5Clog%20bj(o_t)%5C%5C%0As.t.%20%5Csum%7Bk%3D1%7D%5EMbj(k)%3D1%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cmax_B%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bj%3D1%7D%5ENP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20b_j%28o_t%29%5C%5C%0As.t.%20%5Csum%7Bk%3D1%7D%5EMbj%28k%29%3D1%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A)
%3D%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bj%3D1%7D%5ENP(O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%5Clog%20b_j(o_t)%2B%5Csum%7Bj%3D1%7D%5EN%5Cetaj(1-%5Csum%7Bk%3D1%7D%5EMbj(k))%0A#card=math&code=L%28B%2C%5Ceta%29%3D%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bj%3D1%7D%5ENP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%5Clog%20b_j%28o_t%29%2B%5Csum%7Bj%3D1%7D%5EN%5Cetaj%281-%5Csum%7Bk%3D1%7D%5EMb_j%28k%29%29%0A)

对矩阵的每一个元素求偏导。这里需要注意的是，只有的#card=math&code=bi%28o_t%29)求导不为零，其余的项求导均为零%7D%3D%5Csum%7Bt%3D1%7D%5ET%5Cfrac%7B1%7D%7Bbj(k)%7DP(O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)-%5Ceta_j%3D0%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%20b_j(k)%3D%5Cfrac%7B1%7D%7B%5Ceta_j%7D%5Csum%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)%5C%5C%0A%26%5CRightarrow%5Csum%7Bk%3D1%7D%5EMbj(k)%3D%5Csum%7Bk%3D1%7D%5EM%5Cfrac%7B1%7D%7B%5Cetaj%7D%5Csum%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%5CRightarrow%5Ceta_j%26%3D%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bk%3D1%7D%5EMP(O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%5Csum%7Bk%3D1%7D%5EMI(ot%3Dv_k)%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cfrac%7B%5Cpartial%20L%7D%7B%5Cpartial%20b_j%28k%29%7D%3D%5Csum%7Bt%3D1%7D%5ET%5Cfrac%7B1%7D%7Bbj%28k%29%7DP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29-%5Ceta_j%3D0%5C%5C%0A%5Cbegin%7Baligned%7D%0A%26%5CRightarrow%20b_j%28k%29%3D%5Cfrac%7B1%7D%7B%5Ceta_j%7D%5Csum%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29%5C%5C%0A%26%5CRightarrow%5Csum%7Bk%3D1%7D%5EMbj%28k%29%3D%5Csum%7Bk%3D1%7D%5EM%5Cfrac%7B1%7D%7B%5Cetaj%7D%5Csum%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29%5C%5C%0A%26%5Cbegin%7Baligned%7D%0A%5CRightarrow%5Ceta_j%26%3D%5Csum%7Bt%3D1%7D%5ET%5Csum%7Bk%3D1%7D%5EMP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29%5C%5C%0A%26%3D%5Csum%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%5Csum%7Bk%3D1%7D%5EMI%28o_t%3Dv_k%29%0A%5Cend%7Baligned%7D%0A%5Cend%7Baligned%7D%0A%5Cend%7Bgathered%7D%0A)

因为在确定的时候，观测变量等于哪个是确定的，于是对于每一个都显然有%3D1#card=math&code=%5Csum%5Climits%7Bk%3D1%7D%5EMI%28o_t%3Dv_k%29%3D1)，于是可以化简为%7D)%0A#card=math&code=%5Ceta_j%3D%5Csum%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%0A)
%7D(k)%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%7D%0A#card=math&code=b_j%5E%7B%28s%2B1%29%7D%28k%29%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%7D%0A)

Baum-Welch算法

(1)初始化参数%7D%3D(%5Cpi%5E%7B(0)%7D%2CA%5E%7B(0)%7D%2CB%5E%7B(0)%7D)#card=math&code=%5Clambda%5E%7B%280%29%7D%3D%28%5Cpi%5E%7B%280%29%7D%2CA%5E%7B%280%29%7D%2CB%5E%7B%280%29%7D%29)
(2)对进行迭代计算

%7D%3D%5Cfrac%7BP(i1%3Dq_i%2CO%7C%5Clambda%5E%7B(s)%7D)%7D%7BP(O%7C%5Clambda%5E%7B(s)%7D)%7D%5C%5C%0A%5C%5C%0Aa%7Bij%7D%5E%7B(s%2B1)%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP(O%2Cit%3Dq_i%7C%5Clambda%5E%7B(s)%7D)%7D%5C%5C%0A%5C%5C%0Ab_j%5E%7B(s%2B1)%7D(k)%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)I(o_t%3Dv_k)%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%7D%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cpi%7Bi%7D%5E%7B%28s%2B1%29%7D%3D%5Cfrac%7BP%28i1%3Dq_i%2CO%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7BP%28O%7C%5Clambda%5E%7B%28s%29%7D%29%7D%5C%5C%0A%5C%5C%0Aa%7Bij%7D%5E%7B%28s%2B1%29%7D%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B%28s%29%7D%29%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5E%7BT-1%7DP%28O%2Cit%3Dq_i%7C%5Clambda%5E%7B%28s%29%7D%29%7D%5C%5C%0A%5C%5C%0Ab_j%5E%7B%28s%2B1%29%7D%28k%29%3D%5Cfrac%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP%28O%2Cit%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29I%28o_t%3Dv_k%29%7D%7B%5Csum%5Climits%7Bt%3D1%7D%5ETP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%7D%0A%5Cend%7Bgathered%7D%0A)

其中%7D)%2CP(O%2Cit%3Dq_j%7C%5Clambda%5E%7B(s)%7D)%2CP(O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dqj%7C%5Clambda%5E%7B(s)%7D)#card=math&code=P%28O%7C%5Clambda%5E%7B%28s%29%7D%29%2CP%28O%2Ci_t%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29%2CP%28O%2Ci%7Bt%7D%3Dqi%2Ci%7Bt%2B1%7D%3Dq_j%7C%5Clambda%5E%7B%28s%29%7D%29)可由前后向算法计算得出
(3)重复步骤(2)直到模型参数收敛，迭代终止得到模型参数%7D%3D(%5Cpi%5E%7B(s%2B1)%7D%2CA%5E%7B(s%2B1)%7D%2CB%5E%7B(s%2B1)%7D)#card=math&code=%5Clambda%5E%7B%28s%2B1%29%7D%3D%28%5Cpi%5E%7B%28s%2B1%29%7D%2CA%5E%7B%28s%2B1%29%7D%2CB%5E%7B%28s%2B1%29%7D%29)

预测问题

预测问题的本质是求对应最有可能的状态序列，即使#card=math&code=P%28I%7CO%2C%5Clambda%29)最大的状态序列。而对于每一个时刻有，那么可以画出如下图

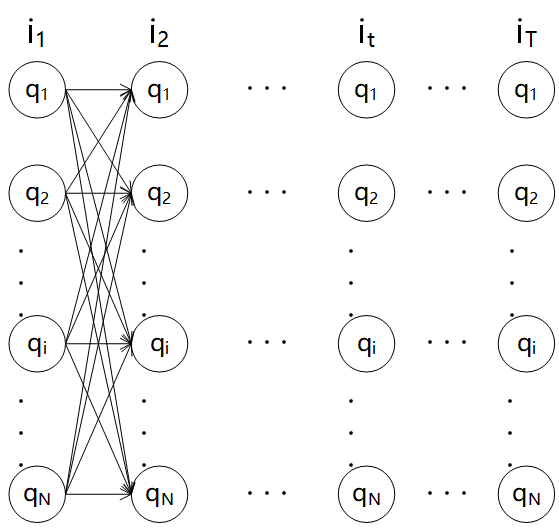图中每一个状态都有N种取值，箭头即可表示状态转移的路径，那么问题就转化为在这些路径中找到最有可能的一条路径。这显然是一个动态规划问题。最直接的想法当然是把所有路径的概率都计算出来，然后比较大小取概率最大的那一条路径，但是这样计算复杂度极高，为#card=math&code=O%28N%5ET%29)。下面介绍动态规划里面的一种方法，维特比算法

维特比算法

一般地，对于类似HMM的网络，每个状态取值不一定是相同的。假设有T个状态，每个状态对应的取值个数为，可画出如下图，这种网络称为篱笆网络

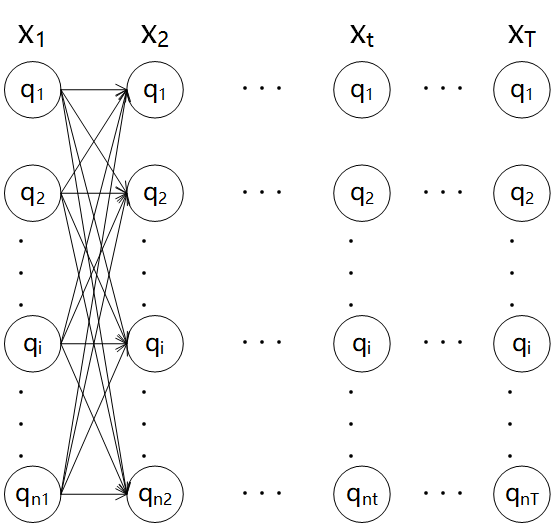对于选择路径，有如下两个事实

1. 显而易见，如果最短路径经过某个点，比如图中状态的点，那么这条路径上从起点到该点的子路径一定是起点到该点的最短路径
2. 如果记录了从起点到某个时刻所有节点的最短路径，那么最终最短路径一定经过其中一条

综合以上两个基本事实，在我们从时刻转移到时刻时，从起点到时刻的所有节点的最短路径是已经找到并记录的，那么在计算从起点到时刻某个节点的最短路径时，只要考虑从起点到时刻的所有节点的最短路径，以及这个从时刻的所有节点到时刻某个节点的最短路径即可，这就是维特比算法的基本思想
维特比算法就是用来解决篱笆网络最优路径问题的。下面描述一下维特比算法的步骤

1. 从起点S出发到第一个状态，其每个节点的概率就是到每个节点的最短路径，将到每个节点的最短路径记为%3DP(x1%3Dq_i)%2Ci%3D1%2C2%2C%5Ccdots%2Cn_1#card=math&code=d%28S%2Cx%7B1i%7D%29%3DP%28x_1%3Dq_i%29%2Ci%3D1%2C2%2C%5Ccdots%2Cn_1)。根据第二个事实这些路径都要记录下来
2. 对于第二个状态，要计算到每个节点的最短路径。因为#card=math&code=d%28S%2Cx%7B1i%7D%29)已经都记录下来了，于是要针对每个节点计算并找到对应每个节点的最小路径并记录%3D%5Cmini%5Bd(S%2Cx%7B1i%7D)%2Bd(x%7B1i%7D%2Cx%7B2j%7D)%5D%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2Cn2%0A#card=math&code=d%28S%2Cx%7B2j%7D%29%3D%5Cmini%5Bd%28S%2Cx%7B1i%7D%29%2Bd%28x%7B1i%7D%2Cx%7B2j%7D%29%5D%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2Cn_2%0A)

1. 对于第个状态，要计算到每个节点的最短路。因为i%7D)#card=math&code=d%28S%2Cx%7B%28t-1%29i%7D%29)已经都记录下来了，于是要针对每个节点计算并找到对应每个节点的最小路径并记录%3D%5Cmini%5Bd(S%2Cx%7B(t-1)i%7D)%2Bd(x%7B(t-1)i%7D%2Cx%7Btj%7D)%5D%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2Cn2%0A#card=math&code=d%28S%2Cx%7Btj%7D%29%3D%5Cmini%5Bd%28S%2Cx%7B%28t-1%29i%7D%29%2Bd%28x%7B%28t-1%29i%7D%2Cx%7Btj%7D%29%5D%2C%5Cquad%20j%3D1%2C2%2C%5Ccdots%2Cn_2%0A)

1. 以此类推计算下去最终即可求得到状态的最短路径

设中最大的数为，那么计算复杂度为#card=math&code=O%28N%5E2T%29)，显然比遍历的方法大大降低了复杂度
对于HMM的预测问题，采用维特比算法，这时的距离度量其实是概率，要找的路径是使#card=math&code=P%28I%7CO%2C%5Clambda%29)概率最大的路径，又因为

%3D%5Cfrac%7BP(I%2CO%7C%5Clambda)%7D%7BP(O%7C%5Clambda)%7D%0A#card=math&code=P%28I%7CO%2C%5Clambda%29%3D%5Cfrac%7BP%28I%2CO%7C%5Clambda%29%7D%7BP%28O%7C%5Clambda%29%7D%0A)

显然当给定样本时观测序列是确定的，所以求#card=math&code=P%28I%7CO%2C%5Clambda%29)最大就是求#card=math&code=P%28I%2CO%7C%5Clambda%29)最大
定义从起点到时刻状态为即的节点时所有路径中的概率最大值为，对应的路径记录下来

%3D%5Cmax%7Bi_1%2Ci_2%2C%5Ccdots%2Ci%7Bt-1%7D%7DP(it%3Dq_i%2Ci%7Bt-1%7D%2C%5Ccdots%2Ci1%2Co_t%2C%5Ccdots%2Co_1%7C%5Clambda)%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=%5Cdelta_t%28i%29%3D%5Cmax%7Bi1%2Ci_2%2C%5Ccdots%2Ci%7Bt-1%7D%7DP%28it%3Dq_i%2Ci%7Bt-1%7D%2C%5Ccdots%2Ci_1%2Co_t%2C%5Ccdots%2Co_1%7C%5Clambda%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A)

在时刻状态为即时所有路径中的概率最大值为，时刻时#card=math&code=%5Cdeltat%28j%29)转化为状态乘以生成的概率最大值，即

%26%3D%5Cmax%7Bi_1%2Ci_2%2C%5Ccdots%2Ci_t%7DP(i%7Bt%2B1%7D%3Dqi%2Ci_t%2C%5Ccdots%2Ci_1%2Co%7Bt%2B1%7D%2C%5Ccdots%2Co1%7C%5Clambda)%5C%5C%0A%26%3D%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdeltat(j)a%7Bji%7Dbi(o%7Bt%2B1%7D)%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cdelta%7Bt%2B1%7D%28i%29%26%3D%5Cmax%7Bi1%2Ci_2%2C%5Ccdots%2Ci_t%7DP%28i%7Bt%2B1%7D%3Dqi%2Ci_t%2C%5Ccdots%2Ci_1%2Co%7Bt%2B1%7D%2C%5Ccdots%2Co1%7C%5Clambda%29%5C%5C%0A%26%3D%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdeltat%28j%29a%7Bji%7Dbi%28o%7Bt%2B1%7D%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Baligned%7D%0A)

对应的的节点所有路径中的概率最大路径前一时刻的节点定义为

%3D%5Carg%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdelta_t(j)a%7Bji%7D%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A#card=math&code=%5CPsi%7Bt%2B1%7D%28i%29%3D%5Carg%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdeltat%28j%29a%7Bji%7D%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A)

因为每个时刻的#card=math&code=%5Cdelta_t%28j%29)都被记录，所以就可以递推得到最终的最大概率路径
HMM中维特比算法的流程

(1)初始化

%3D%5Cpi_ib_i(o_1)%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%5C%5C%0A%5CPsi_1(i)%3D0%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cdelta_1%28i%29%3D%5Cpi_ib_i%28o_1%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%5C%5C%0A%5CPsi_1%28i%29%3D0%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A)

(2)对递推计算

%3D%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdelta%7Bt-1%7D(j)a%7Bji%7Db_i(o_t)%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%5C%5C%0A%5CPsi_t(i)%3D%5Carg%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdelta%7Bt-1%7D(j)a%7Bji%7D%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cdeltat%28i%29%3D%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdelta%7Bt-1%7D%28j%29a%7Bji%7Dbi%28o_t%29%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%5C%5C%0A%5CPsi_t%28i%29%3D%5Carg%5Cmax%7B1%5Cle%20j%5Cle%20N%7D%5Cdelta%7Bt-1%7D%28j%29a%7Bji%7D%2C%5Cquad%20i%3D1%2C2%2C%5Ccdots%2CN%0A%5Cend%7Bgathered%7D%0A)

(3)得到终值

%5C%5C%0AiT%5E*%3D%5Carg%5Cmax%7B1%5Cle%20i%5Cle%20N%7D%5CdeltaT(i)%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0AP%5E%2A%3D%5Cmax%7B1%5Cle%20i%5Cle%20N%7D%5CdeltaT%28i%29%5C%5C%0Ai_T%5E%2A%3D%5Carg%5Cmax%7B1%5Cle%20i%5Cle%20N%7D%5Cdelta_T%28i%29%0A%5Cend%7Bgathered%7D%0A)

(4)最优路径回溯。对

%0A#card=math&code=it%5E%2A%3D%5CPsi%7Bt%2B1%7D%28i_%7Bt%2B1%7D%5E%2A%29%0A)

求得最优路径即最有可能的状态序列