逻辑回归
设二分类样本%5C%7D%7Bi%3D1%7D%5EN%2CX_i%5Cin%5Cmathbb%7BR%7D%5Ep%2Cy_i%5Cin%5C%7B0%2C1%5C%7D#card=math&code=D%3D%5C%7B%28X_i%2Cy_i%29%5C%7D%7Bi%3D1%7D%5EN%2CX_i%5Cin%5Cmathbb%7BR%7D%5Ep%2Cy_i%5Cin%5C%7B0%2C1%5C%7D)
引入一个sigmoid function
%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-z%7D%7D%0A#card=math&code=%5Csigma%28z%29%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-z%7D%7D%0A)
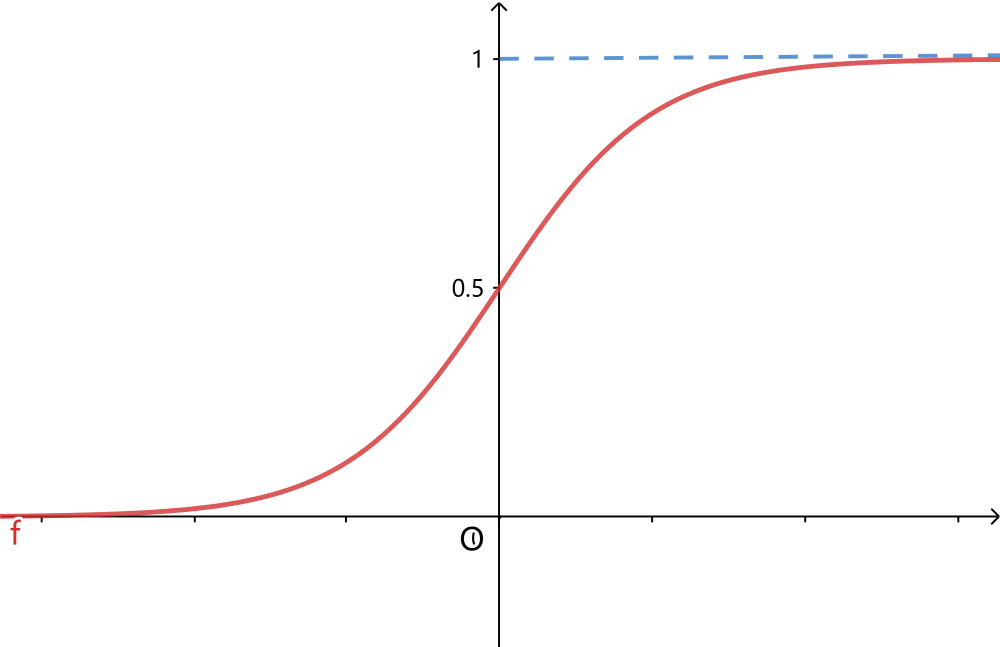
那么逻辑回归模型为
%26%3DP(y%3D1%7CX)%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-W%5ETX%7D%7D%5C%5C%0A1-%5Cpi(X)%26%3DP(y%3D0%7CX)%3D1-p_1%3D%5Cfrac%7Be%5E%7B-W%5ETX%7D%7D%7B1%2Be%5E%7B-W%5ETX%7D%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cpi%28X%29%26%3DP%28y%3D1%7CX%29%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-W%5ETX%7D%7D%5C%5C%0A1-%5Cpi%28X%29%26%3DP%28y%3D0%7CX%29%3D1-p_1%3D%5Cfrac%7Be%5E%7B-W%5ETX%7D%7D%7B1%2Be%5E%7B-W%5ETX%7D%7D%0A%5Cend%7Baligned%7D%0A)
统一起来可写为
%3D%5B%5Cpi(X)%5D%5Ey%5B1-%5Cpi(X)%5D%5E%7B1-y%7D%0A#card=math&code=P%28y%7CX%29%3D%5B%5Cpi%28X%29%5D%5Ey%5B1-%5Cpi%28X%29%5D%5E%7B1-y%7D%0A)
loss function
用极大似然估计的方法
%3D%5Carg%5CmaxW%5Clog%20P(Y%7CX)%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Clog%5Cprod%7Bi%3D1%7D%5ENP(yi%7CX_i)%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Clog%20P(yi%7CX_i)%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Byi%5Clog%20%5Cpi(X_i)%2B(1-y_i)%5Clog%20(1-%5Cpi(X_i))%5D%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Byi%5Clog%5Cfrac%7B%5Cpi(X_i)%7D%7B1-%5Cpi(X_i)%7D%2B%5Clog%20(1-%5Cpi(X_i))%5D%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5ByiW%5ETX_i-%5Clog(1%2B%5Cexp(W%5ETX_i))%5D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Chat%7BW%7D%26%3D%5Carg%5Cmax_WL%28W%29%3D%5Carg%5Cmax_W%5Clog%20P%28Y%7CX%29%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Clog%5Cprod%7Bi%3D1%7D%5ENP%28yi%7CX_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Clog%20P%28yi%7CX_i%29%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Byi%5Clog%20%5Cpi%28X_i%29%2B%281-y_i%29%5Clog%20%281-%5Cpi%28X_i%29%29%5D%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5Byi%5Clog%5Cfrac%7B%5Cpi%28X_i%29%7D%7B1-%5Cpi%28X_i%29%7D%2B%5Clog%20%281-%5Cpi%28X_i%29%29%5D%5C%5C%0A%26%3D%5Carg%5Cmax_W%5Csum%7Bi%3D1%7D%5EN%5By_iW%5ETX_i-%5Clog%281%2B%5Cexp%28W%5ETX_i%29%29%5D%0A%5Cend%7Baligned%7D%0A)
从上面推导可看出,这个损失函数实际为负的交叉熵
求解
这个损失函数的优化问题一般采用梯度下降或者拟牛顿法进行求解,以梯度下降法为例
%7D%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5By_iX_i-%5Cfrac%7BX_i%5Cexp(W%5ETX_i)%7D%7B1%2B%5Cexp(W%5ETX_i)%7D%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5ByiX_i-%5Cfrac%7B1%7D%7B1%2B%5Cexp(-W%5ETX_i)%7DX_i%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Byi-%5Cpi(X_i)%5DX_i%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cnabla%7BL%28W%29%7D%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5By_iX_i-%5Cfrac%7BX_i%5Cexp%28W%5ETX_i%29%7D%7B1%2B%5Cexp%28W%5ETX_i%29%7D%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5Cleft%5ByiX_i-%5Cfrac%7B1%7D%7B1%2B%5Cexp%28-W%5ETX_i%29%7DX_i%5Cright%5D%5C%5C%0A%26%3D%5Csum%7Bi%3D1%7D%5EN%5By_i-%5Cpi%28X_i%29%5DX_i%0A%5Cend%7Baligned%7D%0A)
- 根据梯度下降法,每一轮迭代公式为
%5DXi%5Cquad%5Ceta%5Cin(0%2C1%5D%0A#card=math&code=W%5Cleftarrow%20W%2B%5Ceta%5Csum%7Bi%3D1%7D%5EN%5By_i-%5Cpi%28X_i%29%5DX_i%5Cquad%5Ceta%5Cin%280%2C1%5D%0A)
- 根据随机梯度下降法,每一轮迭代公式为
%5DX_i%5Cquad%5Ceta%5Cin(0%2C1%5D%0A#card=math&code=W%5Cleftarrow%20W%2B%5Ceta%5By_i-%5Cpi%28X_i%29%5DX_i%5Cquad%5Ceta%5Cin%280%2C1%5D%0A)

