S04-降维 - S04P01-主成分分析 - 《机器学习》

主成分分析(PCA)

主成分分析(PCA)

考虑一个问题：正交属性空间中的样本点，如何用一个超平面映射对所有样本进行恰当的表达？
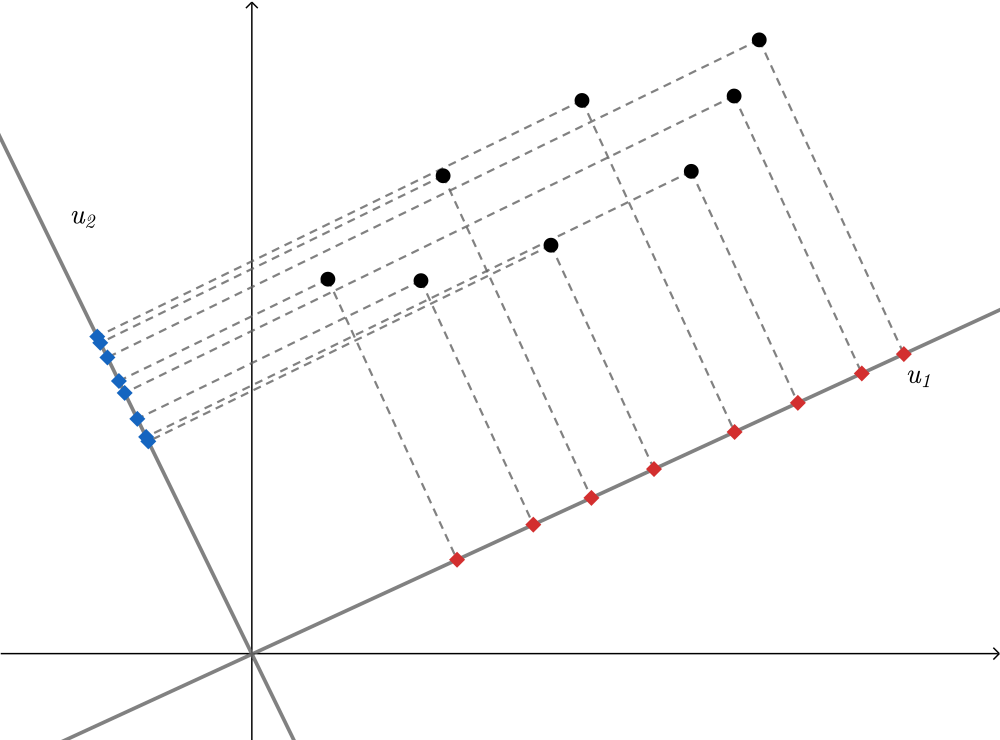
S04P01-主成分分析 - 图1
以二维为例如图， $S04P01-主成分分析 - 图2$ ， $S04P01-主成分分析 - 图3$ 分别为映射为新的平面后的坐标轴方向，显然 $S04P01-主成分分析 - 图4$ 方向上样本的新坐标分布更分散更均匀，而 $S04P01-主成分分析 - 图5$ 方向上样本新坐标趋于相同，那么我们可以忽略 $S04P01-主成分分析 - 图6$ 方向只用 $S04P01-主成分分析 - 图7$ 方向，这样就达到了降维的目的。在高维空间中可能不止一个这样的方向，我们将这样的方向称为主成分。实际上在我们还希望将样本映射到超平面的代价是最小的，那么还应该满足原始空间的样本点到映射超平面的距离最短。对应到图中，如果降维到 $S04P01-主成分分析 - 图8$ 方向，那么尽量使黑点和红点间的距离小
综上得到两个基本原则：

最大可分性：样本点在这个新坐标系某方向的投影尽量分开
最近重构性：样本点到这个新坐标系距离足够近

从上面的分析我们知道PCA实际上是对原始的高维空间样本做一个坐标变换到低维空间，并且这个低维空间满足上述两个基本原则，从而达到降维的目的
给定一个的样本 $S04P01-主成分分析 - 图9$

$S04P01-主成分分析 - 图10$

$S04P01-主成分分析 - 图11$ 为样本的均值向量， $S04P01-主成分分析 - 图12$ 为样本的协方差矩阵

$S04P01-主成分分析 - 图13$ (Xi-%5Cmu)%5ET%0A%5Cend%7Bgathered%7D%0A#card=math&code=%5Cbegin%7Bgathered%7D%0A%5Cmu%3D%5Csum%7Bi%3D1%7D%5ENXi%5C%5C%0A%5CSigma%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%28X_i-%5Cmu%29%28X_i-%5Cmu%29%5ET%0A%5Cend%7Bgathered%7D%0A)

最大可分性

如果希望样本点在新坐标系主成分的投影最大，显然就是要求样本在主成分方向投影点的方差最大，所以又称为”最大投影方差“
若将均值向量 $S04P01-主成分分析 - 图14$ 所在的点作为坐标原点即将数据中心化，设要在某个主成分方向上的基向量在样本原始空间表示为 $S04P01-主成分分析 - 图15$ %5ET#card=math&code=W%3D%28w_1%2Cw_2%2C%5Ccdots%2Cw_p%29%5ET)， $S04P01-主成分分析 - 图16$ 。则在该方向投影后的方差为

$S04P01-主成分分析 - 图17$ %5D%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5ENW%5ET(X_i-%5Cmu)(X_i-%5Cmu)%5ETW%5C%5C%0A%26%3DW%5ET%5Cleft(%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN(Xi-%5Cmu)(X_i-%5Cmu)%5ET%5Cright)W%5C%5C%0A%26%3DW%5ET%5CSigma%20W%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AS%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5BW%5ET%28Xi-%5Cmu%29%5D%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5ENW%5ET%28Xi-%5Cmu%29%28X_i-%5Cmu%29%5ETW%5C%5C%0A%26%3DW%5ET%5Cleft%28%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%28X_i-%5Cmu%29%28X_i-%5Cmu%29%5ET%5Cright%29W%5C%5C%0A%26%3DW%5ET%5CSigma%20W%0A%5Cend%7Baligned%7D%0A)

于是转化为如下优化问题

$S04P01-主成分分析 - 图18$

利用拉格朗日乘子法令 $S04P01-主成分分析 - 图19$ #card=math&code=L%3DW%5ET%5CSigma%20W%2B%5Clambda%281-W%5ETW%29)

$S04P01-主成分分析 - 图20$

上式即可看出 $S04P01-主成分分析 - 图21$ 为协方差矩阵 $S04P01-主成分分析 - 图22$ 的特征值， $S04P01-主成分分析 - 图23$ 为 $S04P01-主成分分析 - 图24$ 的特征向量，于是对 $S04P01-主成分分析 - 图25$ 进行特征值分解即可。将上式带入方差得

$S04P01-主成分分析 - 图26$

那么使得方差最大的主成分即 $S04P01-主成分分析 - 图27$ 最大的特征值对应的特征向量，方差其次大的为第二大的特征值对应的特征向量。而矩阵的特征向量是相互正交的，可作为一组正交基，假设我们最终想要从p维降至q维，那么降维后的坐标系基向量组即为 $S04P01-主成分分析 - 图28$ 的特征值从大到小排列后对应的前q个特征向量组

最近重构性

如果希望样本点重构到新坐标系的代价最小，就是要求样本点到新坐标系的距离最近，所以又称为”最小重构距离“
对于一个样本点 $S04P01-主成分分析 - 图29$ ，设其在新的q维坐标系中为 $S04P01-主成分分析 - 图30$ 。令 $S04P01-主成分分析 - 图31$ #card=math&code=W%3D%28W1%2CW_2%2C%5Ccdots%2CW_q%2CW%7Bq%2B1%7D%2C%5Ccdots%2CW_p%29)，其中 $S04P01-主成分分析 - 图32$ 为变换坐标后每一维的基向量， $S04P01-主成分分析 - 图33$ 。将样本用新基向量表示出来则有

$S04P01-主成分分析 - 图34$ Wj%5C%5C%0A%5Chat%7BX_i%7D%26%3D%5Csum%5Climits%7Bj%3D1%7D%5EqWj%5ET(X_i-%5Cmu)W_j%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AX_i%26%3D%5Csum%5Climits%7Bj%3D1%7D%5EpWj%5ET%28X_i-%5Cmu%29W_j%5C%5C%0A%5Chat%7BX_i%7D%26%3D%5Csum%5Climits%7Bj%3D1%7D%5EqW_j%5ET%28X_i-%5Cmu%29W_j%0A%5Cend%7Baligned%7D%0A)

原始样本点和变换后样本点的距离为 $S04P01-主成分分析 - 图35$ ，那么平均重构距离为 $S04P01-主成分分析 - 图36$

$S04P01-主成分分析 - 图37$ Wj-%5Csum%5Climits%7Bj%3D1%7D%5EqWj%5ET(X_i-%5Cmu)W_j%5Cright)%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5Cleft(%5Csum%7Bj%3Dq%2B1%7D%5EpW_j%5ET(X_i-%5Cmu)W_j%5Cright)%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3Dq%2B1%7D%5Ep(W_j%5ET(X_i-%5Cmu))%5E2%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5Ep%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5ENW_j%5ET(X_i-%5Cmu)(X_i-%5Cmu)%5ETW_j%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5EpWj%5ET%5Cleft(%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN(Xi-%5Cmu)(X_i-%5Cmu)%5ET%5Cright)W_j%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5EpWj%5ET%5CSigma%20W_j%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Ad%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%7C%7CXi-%5Chat%7BX_i%7D%7C%7C%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5Cleft%28%5Csum%7Bj%3D1%7D%5EpW_j%5ET%28X_i-%5Cmu%29W_j-%5Csum%5Climits%7Bj%3D1%7D%5EqWj%5ET%28X_i-%5Cmu%29W_j%5Cright%29%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5Cleft%28%5Csum%7Bj%3Dq%2B1%7D%5EpW_j%5ET%28X_i-%5Cmu%29W_j%5Cright%29%5E2%5C%5C%0A%26%3D%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%5Csum%7Bj%3Dq%2B1%7D%5Ep%28W_j%5ET%28X_i-%5Cmu%29%29%5E2%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5Ep%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5ENW_j%5ET%28X_i-%5Cmu%29%28X_i-%5Cmu%29%5ETW_j%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5EpWj%5ET%5Cleft%28%7B1%5Cover%20N%7D%5Csum%7Bi%3D1%7D%5EN%28Xi-%5Cmu%29%28X_i-%5Cmu%29%5ET%5Cright%29W_j%5C%5C%0A%26%3D%5Csum%7Bj%3Dq%2B1%7D%5EpW_j%5ET%5CSigma%20W_j%0A%5Cend%7Baligned%7D%0A)

于是转化为如下优化问题

$S04P01-主成分分析 - 图38$

根据拉格朗日乘子法令 $S04P01-主成分分析 - 图39$ #card=math&code=L%3D%5Csum%7Bj%3Dq%2B1%7D%5EpW_j%5ET%5CSigma%20W_j%2B%5Csum%7Bj%3Dq%2B1%7D%5Ep%5Clambda_j%281-W_j%5ETW_j%29)

$S04P01-主成分分析 - 图40$

显然 $S04P01-主成分分析 - 图41$ 为 $S04P01-主成分分析 - 图42$ 的特征值， $S04P01-主成分分析 - 图43$ 为对应的特征向量，代入原式

$S04P01-主成分分析 - 图44$

若要使其最小化，就要取 $S04P01-主成分分析 - 图45$ 最小的 $S04P01-主成分分析 - 图46$ 个特征值。因此将数据从p维降至q维需先求 $S04P01-主成分分析 - 图47$ 的特征值，为了满足最小重构距离，必须让 $S04P01-主成分分析 - 图48$ 个特征值最小的特征向量不在作为新坐标系基向量的q个特征向量向量之中。这本质上与用最大投影方差的方法结果是完全等价的

奇异值分解(SVD)

我们知道对于一个中心矩阵 $S04P01-主成分分析 - 图49$ ，矩阵即 $S04P01-主成分分析 - 图50$ 的中心化以后的矩阵，协方差矩阵 $S04P01-主成分分析 - 图51$ 。对 $S04P01-主成分分析 - 图52$ 做奇异值分解有

$S04P01-主成分分析 - 图53$

$S04P01-主成分分析 - 图54$ 显然为一个对角阵，因此对 $S04P01-主成分分析 - 图55$ 做特征值分解可以转化为对 $S04P01-主成分分析 - 图56$ 中心化后的矩阵做奇异值分解