S06P05-条件随机场

条件随机场

定义

条件随机场定义

设$X$和$Y$是随机变量，$P(Y|X)$为条件概率。若随机变量$Y$构成一个无向图$G=(V,E)$表示的马尔科夫随机场，且
$$
P(Yv|X,Y{w\ne v})=P(Yv|X,Y{w\sim v})
$$
对任意节点$v$都成立，则称条件概率$P(Y|X)$为条件随机场。$w\sim v$表示与节点$v$有边连接的所有节点$w$，$w\ne v$表示节点$v$以外的所有节点
这个定义的含义其实就是任意一个节点的条件概率与和该节点没有边连接的节点无关

线性链式条件随机场

条件随机场的定义并没有对$X,Y$的图结构做约束，但是在现实中一般要求$X,Y$有相同的图结构，而且主要考虑线性链式结构，如下两种

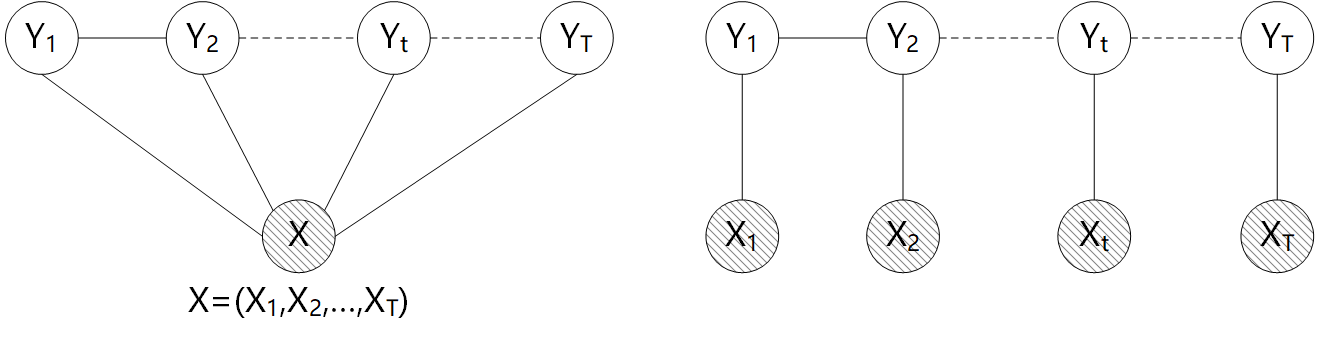设$X=(X1,X_2,\cdots,X_T)$，$Y=(Y_1,Y_2,\cdots,Y_T)$均为线性链表示的随机变量序列，若在给定$X$的条件下$Y$的条件概率分布$P(Y|X)$满足条件随机场即
$$
\begin{gathered}
P(Y_t|X,Y_1,\cdots,Y{t-1},Y{t+1},\cdots,Y_T)=P(Y_t|X,Y{t-1},Y_{t+1})\
t=1,2,\cdots,T(在t=1和T时只考虑单边)
\end{gathered}
$$
称$P(Y|X)$为线性链式条件随机场，$X$为观测序列，$Y$表示状态序列即隐变量

条件随机场参数形式

这里及后面讨论所指的条件随机场均是指线性链式条件随机场
根据概率无向图的因子分解，线性链式条件随机场的最大团显然就是每相邻的两个节点构成的团，因此一共有$T-1$个最大团。事实上为了表达的方便一般假设存在一个$Y0=start$，于是可以写出下式
$$
P(Y|X)=\frac{1}{Z}\exp\left[\sum{t=1}^TFt(Y{t-1},Yt,X)\right]
$$
其中$Z$为归一化因子，$Z=\sum\limits{Y}\exp\left[\sum\limits{t=1}^TF_t(Y{t-1},Yt,X)\right]$
因为每一个最大团的结构都是相同的，所以没有必要为每一个最大团单独设置一个$F_t$，简单的做法是都设为相同的函数，即
$$
P(Y|X)=\frac{1}{Z}\exp\left[\sum{t=1}^TF(Y_{t-1},Y_t,X)\right]
$$

特征函数

特征函数其实就是我们用来表示实际场景中样本某种特征的函数，其函数值为0和1，满足某特征为1，否则为0。例如在词性标注问题中，一句话可以看做$X$，每个词的词性可以看做隐变量$Y$，那么前一个词即$Y{t-1}$，后一个词即$Y_t$，显然根据我们的经验动词后面一般接名词，而动词后面接动词的情况几乎没有，根据这两个经验就可以定义出两个特征函数$f_1(Y{t-1},Yt,X)$和$f_2(Y{t-1},Yt,X)$。$f_1(Y{t-1},Yt,X)$就代表动词后接名词的特征，接名词时为1，否则为0；$f_1(Y{t-1},Yt,X)$就代表动词后接动词的特征，接动词时为1，否则为0。当然对于每一个节点而言其特征函数不光只有该节点与前一个节点的关系的函数，还包括该节点本身的特征函数即$g(Y_t,X)$。$f(Y{t-1},Yt,X)$称为转移特征函数，$g(Y_t,X)$称为状态特征函数。由这些特征函数就组成了上述$F(Y{t-1},Yt,X)$
还是看刚才的词性标注问题，因为动词后接动词是少见的情况，含义其实就是出现这种情况的概率低，那么根据上述条件概率函数，对应的特征函数应该使概率值降低，所以这个特征函数应该有一个负的权值。实际上每一个特征函数都有对应的权值，那么根据前述内容可以写出最终的条件概率密度函数
$$
P(Y|X)=\frac{1}{Z}\exp\left[\sum{t=1}{K1}\lambda_kf_k(Y{t-1},Yt,X)+\sum{l=1}^{K_2}\mu_lg_l(Y_t,X)\right)\right]
$$
上式即为条件随机场条件概率密度函数的参数形式。其中$K_1$为转移特征函数的数目，$\lambda_k$为其权值；$K_2$为状态特征函数的数目，$\mu_k$为其权值
根据前面举的关于词性标注的例子，这样来表达条件概率是十分符合直观的，而构造出好的特征函数就对于条件随机场十分重要，而且由于特征函数的存在，使得条件随机场很灵活，可以针对具体问题构造各种各样的特征函数

条件随机场向量形式

把参数形式中的各个量用向量形式写出
$$
\begin{gathered}
X=\begin{pmatrix}X1\X_2\vdots\X_T\end{pmatrix}\qquad
Y=\begin{pmatrix}Y_1\Y_2\vdots\Y_T\end{pmatrix}\
\
\lambda=\begin{pmatrix}\lambda_1\lambda_2\vdots\lambda{K1}\end{pmatrix}\qquad
\mu=\begin{pmatrix}\mu_1\mu_2\vdots\mu{K2}\end{pmatrix}\
\
f=f(Y_t,Y{t-1},X)=\begin{pmatrix}f1\f_2\vdots\f{K1}\end{pmatrix}\qquad
g=g(Y_t,X)=\begin{pmatrix}g_1\g_2\vdots\g{K2}\end{pmatrix}
\end{gathered}
$$
将上面的式子代入即得
$$
\begin{aligned}
P(Y|X)&=\frac{1}{Z(X,\lambda,\mu)}\exp\sum{t=1}Tf(Yt,Y{t-1},X)+\mu^Tg(Yt,X)]\
&=\frac{1}{Z(X,\lambda,\mu)}\exp\left[\lambdaTf(Y_t,Y{t-1},X)+\muTg(Yt,X)\right]
\end{aligned}
$$
还可以继续统一，$\lambda,\mu$统一为参数$\theta$，$f,g$统一为特征函数$H,F$。令$K=K_1+K_2$
$$
\begin{gathered}
\theta=\begin{pmatrix}\lambda\mu\end{pmatrix}{(K1+K_2)\times1}=\begin{pmatrix}\theta_1\theta_2\vdots\theta_K\end{pmatrix}\
\
H=H(Y_t,Y{t-1},X)=\begin{pmatrix}\sum\limits{t=1}Tg(Y_t,X)\end{pmatrix}{(K1+K_2)\times1}=\sum\limits{t=1}TF(Yt,Y{t-1},X)
\end{gathered}
$$
最终可以写为
$$
\begin{aligned}
P(Y|X)&=\frac{1}{Z(X,\theta)}\exp[\theta^TH(Yt,Y{t-1},X)]\
&=\frac{1}{Z(X,\theta)}\exp[\theta\cdot H(Yt,Y{t-1},X)]
\end{aligned}
$$
这个形式也称为内积形式

条件随机场矩阵形式

设每个状态有$m$种取值，即令$Yt\in(s_1,s_2,\cdots,s_m)$，那么定义一个$m\times m$的矩阵$\Psi$
$$
\begin{aligned}
\Psi_t(X)&=[\Psi_t(Y{t-1}=si,Y_t=s_j,X)]{m\times m}=\left[\exp\left(\sum{k=1}^K\theta_kF_k(Y{t-1}=si,Y_t=s_j,X)\right)\right]{m\times m}\
&=\begin{pmatrix}
\Psit(Y{t-1}=s1,Y_t=s_1,X)&\Psi_t(Y{t-1}=s1,Y_t=s_2,X)&\cdots&\Psi_t(Y{t-1}=s1,Y_t=s_m,X)\
\Psi_t(Y{t-1}=s2,Y_t=s_1,X)&\Psi_t(Y{t-1}=s2,Y_t=s_2,X)&\cdots&\Psi_t(Y{t-1}=s2,Y_t=s_m,X)\
\vdots&\vdots&\ddots&\vdots\
\Psi_t(Y{t-1}=sm,Y_t=s_1,X)&\Psi_t(Y{t-1}=sm,Y_t=s_2,X)&\cdots&\Psi_t(Y{t-1}=sm,Y_t=s_m,X)
\end{pmatrix}
\end{aligned}
$$
其中$i,j=1,2,\cdots,m$，矩阵元素即每一对$Y_t,Y{t-1}$对应的最大团势函数值构成的矩阵
前面我们引入了一个起点$Y0=start$，则有
$$
\begin{aligned}
P(Y|X)&=\frac{1}{Z(X,\theta)}\prod{t=1}^T\Psit(Y{t-1},Y_t,X)
\end{aligned}
$$

概率计算问题

首先讨论边缘概率$P(Y_t=s_i|X)$计算问题

直接计算法

$$
\begin{aligned}
P(Yt=s_i|X)&=\sum{Y1,\cdots,Y{t-1},Y{t+1},\cdots,Y_T}P(Y|X)\
&=\sum{Y1,\cdots,Y{t-1},Y{t+1},\cdots,Y_T}\frac{1}{Z(X,\theta)}\prod{t-1},Y_{t^},X)
\end{aligned}
$$
直接计算的计算复杂度显然达到了指数级，因此需要寻求更简便的算法

前向-后向算法

$$
\begin{aligned}
P(Yt=s_i|X)&=\frac{1}{Z}\sum{Y1,\cdots,Y{t-1},Y{t+1},\cdots,Y_T}\prod{t-1},Y_{t^},X)\
&=\frac{1}{Z}\sum{Y_1,\cdots,Y{t-1},Y{t+1},\cdots,Y_T}\Psi_1(Y_0,Y_1,X)\cdots\Psi_t(Y{t-1},Yt=s_i,X)\Psi{t+1}(Yt=s_i,Y{t+1},X)\cdots\PsiT(Y{T-1},YT,X)\
&=\frac{1}{Z}\left[\sum{Y1,\cdots,Y{t-1}}\Psi1(Y_0,Y_1,X)\cdots\Psi_t(Y{t-1},Yt=s_i,X)\right]\left[\sum{Y{t+1},\cdots,Y_T}\Psi{t+1}(Yt=s_i,Y{t+1},X)\cdots\PsiT(Y{T-1},YT,X)\right]\
&=\frac{1}{Z}\Delta_1\Delta_2
\end{aligned}
$$
先看左边部分，这个求和是可以一步一步来求的，比如先把跟$Y_0$相关的项$\Psi_1(Y_0,Y_1,X)$求和，这样这一项的$Y_0$就消掉了，只剩下$Y_1$，就能和$\Psi_2(Y_1,Y_2,X)$构成只关于$Y_1$的项，然后再求和消去$Y_1$，后面的计算方法以此类推，这样就构成了递推
$$
\begin{aligned}
\Delta_1&=\sum{Y1,\cdots,Y{t-1}}\Psi1(Y_0,Y_1,X)\cdots\Psi_t(Y{t-1},Yt=s_i,X)\
&=\sum{Y2,\cdots,Y{t-1}}\Psit(Y{t-1},Yt=s_i,X)\cdots\Psi_3(Y_2,Y_3,X)\left(\sum{Y1}\Psi_2(Y_1,Y_2,X)\Psi_1(Y_0,Y_1,X)\right)\
&=\sum{Y3,\cdots,Y{t-1}}\Psit(Y{t-1},Yt=s_i,X)\cdots\Psi_4(Y_3,Y_4,X)\left(\sum{Y2}\Psi_3(Y_2,Y_3,X)\left(\sum{Y1}\Psi_2(Y_1,Y_2,X)\Psi_1(Y_0,Y_1,X)\right)\right)\
&=\cdots\
&=\sum{Y{t-1}}\Psi_t(Y{t-1},Yt=s_i,X)\left(\cdots\left(\sum{Y2}\Psi_3(Y_2,Y_3,X)\left(\sum{Y1}\Psi_2(Y_1,Y_2,X)\Psi_1(Y_0,Y_1,X)\right)\right)\cdots\right)
\end{aligned}
$$
根据上式显然可以写出递推式
$$
\begin{aligned}
\alpha_t(Y_t=s_i)&=\sum{Y{t-1}}\Psi_t(Y{t-1},Yt=s_i,X)\alpha{t-1}(Y{t-1})\
&=\Psi_t(Y{t-1}=s1,Y_t,X)\alpha{t-1}(Y{t-1}=s_1)+\Psi_t(Y{t-1}=s2,Y_t,X)\alpha{t-1}(Y{t-1}=s_2)+\cdots+\Psi_t(Y{t-1}=sm,Y_t=s_i,X)\alpha{t-1}(Y{t-1}=s_m)\
&=\begin{pmatrix}\alpha{t-1}(Y{t-1}=s_1)&\alpha{t-1}(Y{t-1}=s_2)&\cdots&\alpha{t-1}(Y{t-1}=s_m)\end{pmatrix}
\begin{pmatrix}\Psi_t(Y{t-1}=s1,Y_t=s_i,X)\Psi_t(Y{t-1}=s2,Y_t=s_i,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_i,X)\end{pmatrix}
\end{aligned}
$$
如果将$\alpha{t-1}(Y{t-1})=\begin{pmatrix}\alpha{t-1}(Y{t-1}=s_1)&\alpha{t-1}(Y{t-1}=s_2)&\cdots&\alpha{t-1}(Y{t-1}=s_m)\end{pmatrix}^T$作为一个列向量，那么可将上式写为
$$
\begin{aligned}
\alpha_t(Y_t=s_i)&=\alpha{t-1}^T(Y{t-1})\begin{pmatrix}\Psi_t(Y{t-1}=s1,Y_t=s_i,X)\Psi_t(Y{t-1}=s2,Y_t=s_i,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_i,X)\end{pmatrix}
\end{aligned}
$$
同样将$\alpha_t(Y_t)=\begin{pmatrix}\alpha_t(Y_t=s_1)&\alpha_t(Y_t=s_2)&\cdots&\alpha_t(Y_t=s_m)\end{pmatrix}^T$作为一个列向量，于是根据上式有
$$
\begin{aligned}
\alpha_t^T(Y_t)&=\begin{pmatrix}\alpha_t(Y_t=s_1)&\alpha_t(Y_t=s_2)&\cdots&\alpha_t(Y_t=s_m)\end{pmatrix}\
&=\begin{pmatrix}\alpha{t-1}T(Y{t-1})\begin{pmatrix}\Psi_t(Y{t-1}=s1,Y_t=s_2,X)\Psi_t(Y{t-1}=s2,Y_t=s_2,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_2,X)\end{pmatrix}&\cdots&\alpha{t-1}^T(Y{t-1})\begin{pmatrix}\Psi_t(Y{t-1}=s1,Y_t=s_m,X)\Psi_t(Y{t-1}=s2,Y_t=s_m,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_m,X)\end{pmatrix}\end{pmatrix}\
&=\alpha{t-1}^T(Y{t-1})\begin{pmatrix}\begin{matrix}\Psi_t(Y{t-1}=s1,Y_t=s_1,X)\Psi_t(Y{t-1}=s2,Y_t=s_1,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_1,X)\end{matrix}&\begin{matrix}\Psi_t(Y{t-1}=s1,Y_t=s_2,X)\Psi_t(Y{t-1}=s2,Y_t=s_2,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_2,X)\end{matrix}&\cdots&\begin{matrix}\Psi_t(Y{t-1}=s1,Y_t=s_m,X)\Psi_t(Y{t-1}=s2,Y_t=s_m,X)\vdots\Psi_t(Y{t-1}=sm,Y_t=s_m,X)\end{matrix}\end{pmatrix}\
&=\alpha{t-1}^T(Y{t-1})\Psi_t(X)
\end{aligned}
$$
对于初始值，一般会令$Y_0=s_1$等特定的值，可任意指定，则有
$$
\alpha_1T(Y_0)=\Psi_1(Y_0,Y_1,X)\alpha_0^T(Y_0)
$$
观察$\Delta_1$的原始式子，即可知令$\alpha_0^T(Y_0)=\alpha_0(Y_0)=1$，然后通过迭代即可计算出$\Delta_1$
同理可以对$\Delta_2$做同样的推导，为了最终结果和左边部分下标保持一致用后向算法
$$
\begin{aligned}
\Delta_2&=\sum{Y{t+1},\cdots,Y_T}\Psi{t+1}(Yt=s_i,Y{t+1},X)\cdots\PsiT(Y{T-1},YT,X)\
&=\sum{Y{t+1},\cdots,Y{T-1}}\Psi{t+1}(Y_t=s_i,Y{t+1},X)\cdots\Psi{T-1}(Y{T-2},Y{T-1},X)\left(\sum{YT}\Psi_T(Y{T-1},YT,X)\right)\
&=\sum{Y{t+1},\cdots,Y{T-2}}\Psi{t+1}(Y_t=s_i,Y{t+1},X)\cdots\Psi{T-2}(Y{T-3},Y{T-2},X)\left(\sum{Y{T-1}}\Psi{T-1}(Y{T-2},Y{T-1},X)\left(\sum{Y_T}\Psi_T(Y{T-1},YT,X)\right)\right)\
&=\cdots\
&=\sum{Y{t+1}}\Psi{t+1}(Yt=s_i,Y{t+1},X)\cdots\left(\sum{Y{T-2}}\Psi{T-2}(Y{T-3},Y{T-2},X)\left(\sum{Y{T-1}}\Psi{T-1}(Y{T-2},Y{T-1},X)\left(\sum{Y_T}\Psi_T(Y{T-1},YT,X)\right)\right)\cdots\right)
\end{aligned}
$$
递推式
$$
\begin{gathered}
\beta_t(Y_t=s_i)=\sum{Y{t+1}}\Psi{t+1}(Yt=s_i,Y{t+1},X)\beta{t+1}(Y{t+1})\
\end{gathered}
$$
同样写成矩阵形式即
$$
\betat(Y_t)=\Psi{t+1}(X)\beta{t+1}(Y{t+1})
$$
根据$\Delta2$原始式子，初始值
$$
\beta_T(Y_T)=1
$$
于是对于给定的$t$时刻，根据前向-后向算法可得概率
$$
P(Y_t=s_i|X)=\frac{1}{Z(X,\theta)}\alpha_t(Y_t=s_i)\beta_t(Y_t=s_i)
$$
也可以简写为
$$
P(Y_t=s_i|X)=\frac{1}{Z(X,\theta)}\alpha_t(s_i)\beta_t(s_i)
$$
显然有
$$
Z(X,\theta)=\sum{i=1}m\beta1(s_i)
$$
写为矩阵形式
$$
Z(X,\theta)=\alpha_TT\cdot\beta_1(Y_1)
$$
$\mathbf{1}$是元素均为1的列向量
同样的方法可计算$P(Y{t-1}=si,Y_t=s_j|X)$，显然相当于上面的$\Delta_1$求和中少了对$Y{t-1}$求和，因此根据前向算法
$$
\begin{aligned}
\Delta1&=\Psi_t(Y{t-1}=si,Y_t=s_j,X)\left(\sum{Y{t-2}}\Psi{t-1}(Y{t-2},Y{t-1}=sj,X)\cdots\left(\sum{Y2}\Psi_3(Y_2,Y_3,X)\left(\sum{Y1}\Psi_2(Y_1,Y_2,X)\Psi_1(Y_0,Y_1,X)\right)\right)\cdots\right)\
&=\alpha{t-1}(si)\Psi_t(Y{t-1}=si,Y_t=s_j,X)
\end{aligned}
$$
而$\Delta_2$不变，因此有
$$
P(Y{t-1}=si,Y_t=s_j|X)=\frac{1}{Z(X,\theta)}\alpha{t-1}(si)\Psi_t(Y{t-1}=si,Y_t=s_j,X)\beta_t(s_j)
$$
其中$\Psi_t(Y{t-1}=s_i,Y_t=s_j,X)$为矩阵$\Psi_t(X)$中对应的元素

参数学习问题

下面讨论CRF的参数学习。给定训练样本$D={(X{(i)})}{i=1}{(i)},Y^{(i)}$均为$T$维随机变量，那么根据极大似然估计有
$$
\begin{aligned}
\hat{\theta}&=\arg\max\theta\sum{i=1}^N\log P(Y{(i)})\
&=\arg\max\theta\sum{i=1}{(i)},\theta)}\exp[\theta{(i)},Y{t-1}{(i)})]\
&=\arg\max\theta\sum{i=1}TH(Yt{(i)},X^{(i)})-\log Z(X^{(i)},\theta)\right]
\end{aligned}
$$
解决这个最优化问题的方法有梯度下降法、拟牛顿法，改进的迭代尺度算法IIS等，下面推导梯度下降法。令
$$
\begin{aligned}
L&=\sum{i=1}TH(Yt{(i)},X^{(i)})-\log Z(X^{(i)},\theta)\right]\
&=\sum{i=1}TH(Yt{(i)},XN\log Z(X^{(i)},\theta)\
&=L_1-L_2
\end{aligned}
$$
对$\theta$求梯度
$$
\begin{aligned}
\nabla\theta L&=\nabla\theta L_1-\nabla\theta L2\
&=\sum{i=1}{(i)},Y{t-1}{(i)})-\nabla\theta\sum{i=1}^N\log Z(X^{(i)},\theta)
\end{aligned}
$$
观察一下原始的概率函数
$$
\begin{aligned}
P(Y|X)&=\frac{1}{Z(X,\theta)}\exp[\theta^TH(Y_t,Y{t-1},X)]\
&=\exp[\theta^TH(Yt,Y{t-1},X)-\log Z(X,\theta)]
\end{aligned}
$$
显然属于指数族分布，$\log Z(X,\theta)$为对数配分函数，于是根据指数族分布的性质有
$$
\begin{aligned}
\nabla\theta L_2&=\sum{i=1}^N\nabla\theta\log Z(X^{(i)},\theta)\
&=\sum{i=1}{(i)}|X{(i)},Y{t-1}{(i)})]
\end{aligned}
$$
下面探索如何求解这个期望，因为对于每个样本都是一样的，因此下面的推导先不写上标
$$
\begin{aligned}
E{P(Y|X)}[H(Yt,Y{t-1},X)]&=\sumYP(Y|X)H(Y_t,Y{t-1},X)\
&=\sum{Y_1,Y_2,\cdots,Y_T}P(Y|X)\sum{t=1}^TF(Y{t-1},Y_t,X)\
&=\sum{t=1}^T\sum{Y_1,Y_2,\cdots,Y_T}P(Y|X)F(Y{t-1},Yt,X)\
&=\sum{t=1}^T\sum{Y_1}\cdots\sum{Y{t-1}}\sum{Yt}\cdots\sum{YT}P(Y|X)F(Y{t-1},Yt,X)\
&=\sum{t=1}^T\sum{Y{t-1}}\sum{Y_t}F(Y{t-1},Yt,X)\left(\sum{Y1}\cdots\sum{Y{t-2}}\sum{Y{t+1}}\cdots\sum{YT}P(Y|X)\right)\
&=\sum{t=1}^T\sum{Y{t-1}}\sum{Y_t}F(Y{t-1},Yt,X)P(Y{t-1},Yt,X)
\end{aligned}
$$
显然这个结果中$F(Y{t-1},Yt,X)$为特征函数，$P(Y{t-1},Yt,X)$这个边缘概率根据前述推导可以用前后向算法求得，于是期望就表示出来了，代入则有
$$
\nabla\theta L2=\sum{i=1}T\sum{Y{t-1}}\sum{Y_t}F(Y{t-1}{(i)},X{(i)},Yt{(i)})
$$
因此就可以求出梯度
$$
\nabla\theta L=\sum{i=1}T\left(F(Y_t{(i)},X{(i)},Y_t{(i)})P(Y{t-1}{(i)},X^{(i)})\right)
$$
然后根据梯度下降法即可迭代求出参数