3-1,低阶API示范

下面的范例使用TensorFlow的低阶API实现线性回归模型和DNN二分类模型。

低阶API主要包括张量操作，计算图和自动微分。

  1. import tensorflow as tf
  3. #打印时间分割线
  4. @tf.function
  5. def printbar():
  6.     today_ts = tf.timestamp()%(24*60*60)
  8.     hour = tf.cast(today_ts//3600+8,tf.int32)%tf.constant(24)
  9.     minite = tf.cast((today_ts%3600)//60,tf.int32)
  10.     second = tf.cast(tf.floor(today_ts%60),tf.int32)
  12.     def timeformat(m):
  13.         if tf.strings.length(tf.strings.format("{}",m))==1:
  14.             return(tf.strings.format("0{}",m))
  15.         else:
  16.             return(tf.strings.format("{}",m))
  18.     timestring = tf.strings.join([timeformat(hour),timeformat(minite),
  19.                 timeformat(second)],separator = ":")
  20.     tf.print("=========="*8+timestring)

一，线性回归模型

1，准备数据

  1. import numpy as np 
  2. import pandas as pd
  3. from matplotlib import pyplot as plt 
  4. import tensorflow as tf
  7. #样本数量
  8. n = 400
  10. # 生成测试用数据集
  11. X = tf.random.uniform([n,2],minval=-10,maxval=10) 
  12. w0 = tf.constant([[2.0],[-3.0]])
  13. b0 = tf.constant([[3.0]])
  14. Y = X@w0 + b0 + tf.random.normal([n,1],mean = 0.0,stddev= 2.0)  # @表示矩阵乘法,增加正态扰动
  1. # 数据可视化
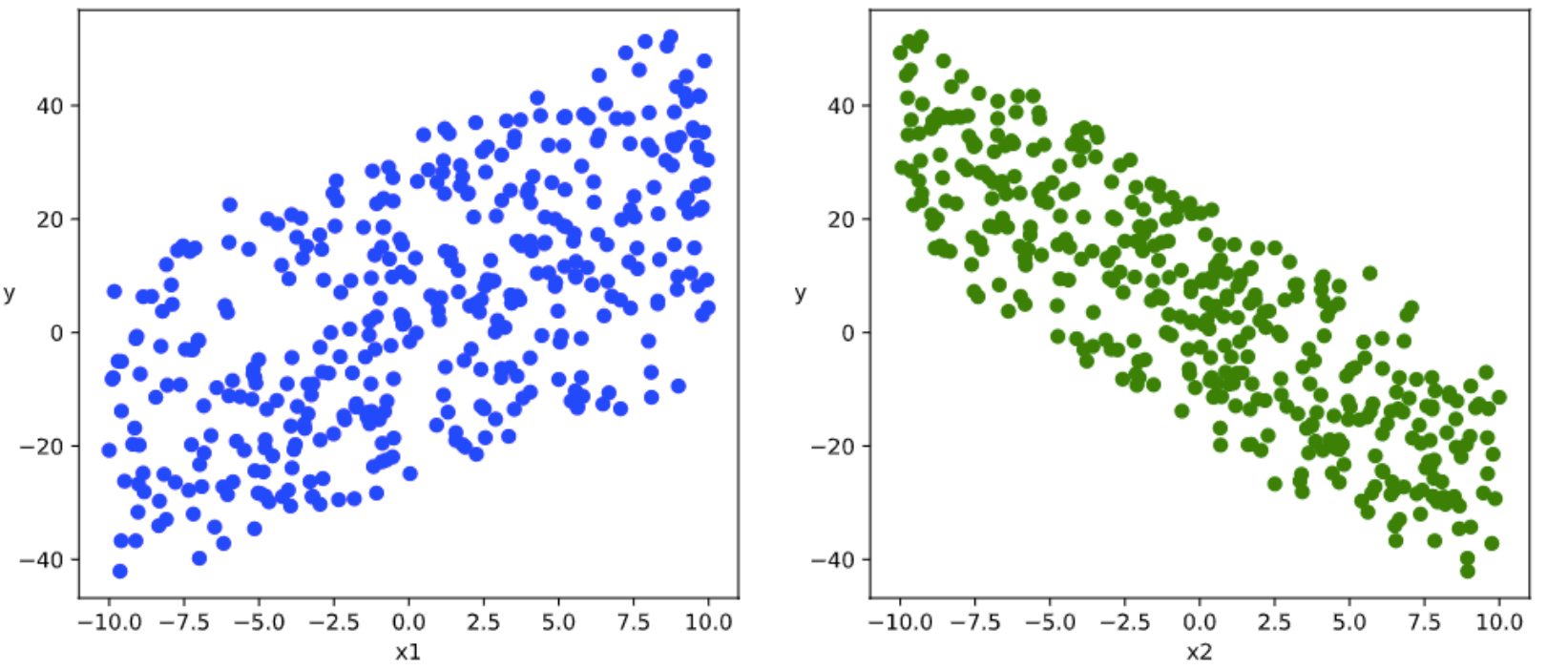
  3. %matplotlib inline
  4. %config InlineBackend.figure_format = 'svg'
  6. plt.figure(figsize = (12,5))
  7. ax1 = plt.subplot(121)
  8. ax1.scatter(X[:,0],Y[:,0], c = "b")
  9. plt.xlabel("x1")
  10. plt.ylabel("y",rotation = 0)
  12. ax2 = plt.subplot(122)
  13. ax2.scatter(X[:,1],Y[:,0], c = "g")
  14. plt.xlabel("x2")
  15. plt.ylabel("y",rotation = 0)
  16. plt.show()

image.png

  1. # 构建数据管道迭代器
  2. def data_iter(features, labels, batch_size=8):
  3.     num_examples = len(features)
  4.     indices = list(range(num_examples))
  5.     np.random.shuffle(indices)  #样本的读取顺序是随机的
  6.     for i in range(0, num_examples, batch_size):
  7.         indexs = indices[i: min(i + batch_size, num_examples)]
  8.         yield tf.gather(features,indexs), tf.gather(labels,indexs)
  10. # 测试数据管道效果   
  11. batch_size = 8
  12. (features,labels) = next(data_iter(X,Y,batch_size))
  13. print(features)
  14. print(labels)
  1. tf.Tensor(
  2. [[ 2.6161194   0.11071014]
  3.  [ 9.79207    -0.70180416]
  4.  [ 9.792343    6.9149055 ]
  5.  [-2.4186516  -9.375019  ]
  6.  [ 9.83749    -3.4637213 ]
  7.  [ 7.3953056   4.374569  ]
  8.  [-0.14686584 -0.28063297]
  9.  [ 0.49001217 -9.739792  ]], shape=(8, 2), dtype=float32)
  10. tf.Tensor(
  11. [[ 9.334667 ]
  12.  [22.058844 ]
  13.  [ 3.0695205]
  14.  [26.736238 ]
  15.  [35.292133 ]
  16.  [ 4.2943544]
  17.  [ 1.6713585]
  18.  [34.826904 ]], shape=(8, 1), dtype=float32)

2，定义模型

  1. w = tf.Variable(tf.random.normal(w0.shape))
  2. b = tf.Variable(tf.zeros_like(b0,dtype = tf.float32))
  4. # 定义模型
  5. class LinearRegression:     
  6.     #正向传播
  7.     def __call__(self,x): 
  8.         return x@w + b
  10.     # 损失函数
  11.     def loss_func(self,y_true,y_pred):  
  12.         return tf.reduce_mean((y_true - y_pred)**2/2)
  14. model = LinearRegression()

3，训练模型

  1. # 使用动态图调试
  2. def train_step(model, features, labels):
  3.     with tf.GradientTape() as tape:
  4.         predictions = model(features)
  5.         loss = model.loss_func(labels, predictions)
  6.     # 反向传播求梯度
  7.     dloss_dw,dloss_db = tape.gradient(loss,[w,b])
  8.     # 梯度下降法更新参数
  9.     w.assign(w - 0.001*dloss_dw)
  10.     b.assign(b - 0.001*dloss_db)
  12.     return loss
  1. # 测试train_step效果
  2. batch_size = 10
  3. (features,labels) = next(data_iter(X,Y,batch_size))
  4. train_step(model,features,labels)
  1. <tf.Tensor: shape=(), dtype=float32, numpy=211.09982>
  1. def train_model(model,epochs):
  2.     for epoch in tf.range(1,epochs+1):
  3.         for features, labels in data_iter(X,Y,10):
  4.             loss = train_step(model,features,labels)
  6.         if epoch%50==0:
  7.             printbar()
  8.             tf.print("epoch =",epoch,"loss = ",loss)
  9.             tf.print("w =",w)
  10.             tf.print("b =",b)
  12. train_model(model,epochs = 200)
  1. ================================================================================16:35:56
  2. epoch = 50 loss =  1.78806472
  3. w = [[1.97554708]
  4.  [-2.97719598]]
  5. b = [[2.60692883]]
  6. ================================================================================16:36:00
  7. epoch = 100 loss =  2.64588404
  8. w = [[1.97319281]
  9.  [-2.97810626]]
  10. b = [[2.95525956]]
  11. ================================================================================16:36:04
  12. epoch = 150 loss =  1.42576694
  13. w = [[1.96466208]
  14.  [-2.98337793]]
  15. b = [[3.00264144]]
  16. ================================================================================16:36:08
  17. epoch = 200 loss =  1.68992615
  18. w = [[1.97718477]
  19.  [-2.983814]]
  20. b = [[3.01013041]]
  1. ##使用autograph机制转换成静态图加速
  3. @tf.function
  4. def train_step(model, features, labels):
  5.     with tf.GradientTape() as tape:
  6.         predictions = model(features)
  7.         loss = model.loss_func(labels, predictions)
  8.     # 反向传播求梯度
  9.     dloss_dw,dloss_db = tape.gradient(loss,[w,b])
  10.     # 梯度下降法更新参数
  11.     w.assign(w - 0.001*dloss_dw)
  12.     b.assign(b - 0.001*dloss_db)
  14.     return loss
  16. def train_model(model,epochs):
  17.     for epoch in tf.range(1,epochs+1):
  18.         for features, labels in data_iter(X,Y,10):
  19.             loss = train_step(model,features,labels)
  20.         if epoch%50==0:
  21.             printbar()
  22.             tf.print("epoch =",epoch,"loss = ",loss)
  23.             tf.print("w =",w)
  24.             tf.print("b =",b)
  26. train_model(model,epochs = 200)
  1. ================================================================================16:36:35
  2. epoch = 50 loss =  0.894210339
  3. w = [[1.96927285]
  4.  [-2.98914337]]
  5. b = [[3.00987792]]
  6. ================================================================================16:36:36
  7. epoch = 100 loss =  1.58621466
  8. w = [[1.97566223]
  9.  [-2.98550248]]
  10. b = [[3.00998402]]
  11. ================================================================================16:36:37
  12. epoch = 150 loss =  2.2695992
  13. w = [[1.96664226]
  14.  [-2.99248481]]
  15. b = [[3.01028705]]
  16. ================================================================================16:36:38
  17. epoch = 200 loss =  1.90848124
  18. w = [[1.98000824]
  19.  [-2.98888135]]
  20. b = [[3.01085401]]
  1. # 结果可视化
  3. %matplotlib inline
  4. %config InlineBackend.figure_format = 'svg'
  6. plt.figure(figsize = (12,5))
  7. ax1 = plt.subplot(121)
  8. ax1.scatter(X[:,0],Y[:,0], c = "b",label = "samples")
  9. ax1.plot(X[:,0],w[0]*X[:,0]+b[0],"-r",linewidth = 5.0,label = "model")
  10. ax1.legend()
  11. plt.xlabel("x1")
  12. plt.ylabel("y",rotation = 0)
  15. ax2 = plt.subplot(122)
  16. ax2.scatter(X[:,1],Y[:,0], c = "g",label = "samples")
  17. ax2.plot(X[:,1],w[1]*X[:,1]+b[0],"-r",linewidth = 5.0,label = "model")
  18. ax2.legend()
  19. plt.xlabel("x2")
  20. plt.ylabel("y",rotation = 0)
  22. plt.show()

image.png

二，DNN二分类模型

1，准备数据

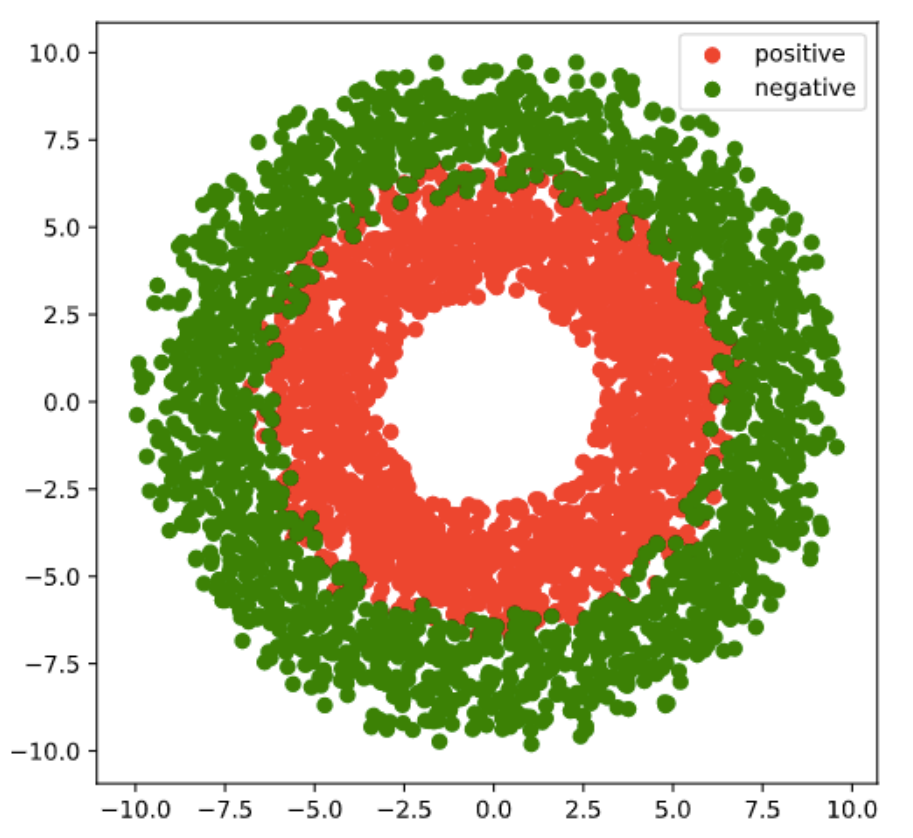
  1. import numpy as np 
  2. import pandas as pd 
  3. from matplotlib import pyplot as plt
  4. import tensorflow as tf
  5. %matplotlib inline
  6. %config InlineBackend.figure_format = 'svg'
  8. #正负样本数量
  9. n_positive,n_negative = 2000,2000
  11. #生成正样本, 小圆环分布
  12. r_p = 5.0 + tf.random.truncated_normal([n_positive,1],0.0,1.0)
  13. theta_p = tf.random.uniform([n_positive,1],0.0,2*np.pi) 
  14. Xp = tf.concat([r_p*tf.cos(theta_p),r_p*tf.sin(theta_p)],axis = 1)
  15. Yp = tf.ones_like(r_p)
  17. #生成负样本, 大圆环分布
  18. r_n = 8.0 + tf.random.truncated_normal([n_negative,1],0.0,1.0)
  19. theta_n = tf.random.uniform([n_negative,1],0.0,2*np.pi) 
  20. Xn = tf.concat([r_n*tf.cos(theta_n),r_n*tf.sin(theta_n)],axis = 1)
  21. Yn = tf.zeros_like(r_n)
  23. #汇总样本
  24. X = tf.concat([Xp,Xn],axis = 0)
  25. Y = tf.concat([Yp,Yn],axis = 0)
  28. #可视化
  29. plt.figure(figsize = (6,6))
  30. plt.scatter(Xp[:,0].numpy(),Xp[:,1].numpy(),c = "r")
  31. plt.scatter(Xn[:,0].numpy(),Xn[:,1].numpy(),c = "g")
  32. plt.legend(["positive","negative"]);

image.png

  1. # 构建数据管道迭代器
  2. def data_iter(features, labels, batch_size=8):
  3.     num_examples = len(features)
  4.     indices = list(range(num_examples))
  5.     np.random.shuffle(indices)  #样本的读取顺序是随机的
  6.     for i in range(0, num_examples, batch_size):
  7.         indexs = indices[i: min(i + batch_size, num_examples)]
  8.         yield tf.gather(features,indexs), tf.gather(labels,indexs)
  10. # 测试数据管道效果   
  11. batch_size = 10
  12. (features,labels) = next(data_iter(X,Y,batch_size))
  13. print(features)
  14. print(labels)
  1. tf.Tensor(
  2. [[ 0.03732629  3.5783494 ]
  3.  [ 0.542919    5.035079  ]
  4.  [ 5.860281   -2.4476354 ]
  5.  [ 0.63657564  3.194231  ]
  6.  [-3.5072308   2.5578873 ]
  7.  [-2.4109735  -3.6621518 ]
  8.  [ 4.0975413  -2.4172943 ]
  9.  [ 1.9393908  -6.782317  ]
  10.  [-4.7453732  -0.5176727 ]
  11.  [-1.4057113  -7.9775257 ]], shape=(10, 2), dtype=float32)
  12. tf.Tensor(
  13. [[1.]
  14.  [1.]
  15.  [0.]
  16.  [1.]
  17.  [1.]
  18.  [1.]
  19.  [1.]
  20.  [0.]
  21.  [1.]
  22.  [0.]], shape=(10, 1), dtype=float32)

2，定义模型

此处范例我们利用tf.Module来组织模型变量，关于tf.Module的较详细介绍参考本书第四章最后一节: Autograph和tf.Module。

  1. class DNNModel(tf.Module):
  2.     def __init__(self,name = None):
  3.         super(DNNModel, self).__init__(name=name)
  4.         self.w1 = tf.Variable(tf.random.truncated_normal([2,4]),dtype = tf.float32)
  5.         self.b1 = tf.Variable(tf.zeros([1,4]),dtype = tf.float32)
  6.         self.w2 = tf.Variable(tf.random.truncated_normal([4,8]),dtype = tf.float32)
  7.         self.b2 = tf.Variable(tf.zeros([1,8]),dtype = tf.float32)
  8.         self.w3 = tf.Variable(tf.random.truncated_normal([8,1]),dtype = tf.float32)
  9.         self.b3 = tf.Variable(tf.zeros([1,1]),dtype = tf.float32)
  12.     # 正向传播
  13.     @tf.function(input_signature=[tf.TensorSpec(shape = [None,2], dtype = tf.float32)])  
  14.     def __call__(self,x):
  15.         x = tf.nn.relu(x@self.w1 + self.b1)
  16.         x = tf.nn.relu(x@self.w2 + self.b2)
  17.         y = tf.nn.sigmoid(x@self.w3 + self.b3)
  18.         return y
  20.     # 损失函数(二元交叉熵)
  21.     @tf.function(input_signature=[tf.TensorSpec(shape = [None,1], dtype = tf.float32),
  22.                               tf.TensorSpec(shape = [None,1], dtype = tf.float32)])  
  23.     def loss_func(self,y_true,y_pred):  
  24.         #将预测值限制在 1e-7 以上, 1 - 1e-7 以下，避免log(0)错误
  25.         eps = 1e-7
  26.         y_pred = tf.clip_by_value(y_pred,eps,1.0-eps)
  27.         bce = - y_true*tf.math.log(y_pred) - (1-y_true)*tf.math.log(1-y_pred)
  28.         return  tf.reduce_mean(bce)
  30.     # 评估指标(准确率)
  31.     @tf.function(input_signature=[tf.TensorSpec(shape = [None,1], dtype = tf.float32),
  32.                               tf.TensorSpec(shape = [None,1], dtype = tf.float32)]) 
  33.     def metric_func(self,y_true,y_pred):
  34.         y_pred = tf.where(y_pred>0.5,tf.ones_like(y_pred,dtype = tf.float32),
  35.                           tf.zeros_like(y_pred,dtype = tf.float32))
  36.         acc = tf.reduce_mean(1-tf.abs(y_true-y_pred))
  37.         return acc
  39. model = DNNModel()
  1. # 测试模型结构
  2. batch_size = 10
  3. (features,labels) = next(data_iter(X,Y,batch_size))
  5. predictions = model(features)
  7. loss = model.loss_func(labels,predictions)
  8. metric = model.metric_func(labels,predictions)
  10. tf.print("init loss:",loss)
  11. tf.print("init metric",metric)
  1. init loss: 1.76568353
  2. init metric 0.6
  1. print(len(model.trainable_variables))
  1. 6

3，训练模型

  1. ##使用autograph机制转换成静态图加速
  3. @tf.function
  4. def train_step(model, features, labels):
  6.     # 正向传播求损失
  7.     with tf.GradientTape() as tape:
  8.         predictions = model(features)
  9.         loss = model.loss_func(labels, predictions) 
  11.     # 反向传播求梯度
  12.     grads = tape.gradient(loss, model.trainable_variables)
  14.     # 执行梯度下降
  15.     for p, dloss_dp in zip(model.trainable_variables,grads):
  16.         p.assign(p - 0.001*dloss_dp)
  18.     # 计算评估指标
  19.     metric = model.metric_func(labels,predictions)
  21.     return loss, metric
  24. def train_model(model,epochs):
  25.     for epoch in tf.range(1,epochs+1):
  26.         for features, labels in data_iter(X,Y,100):
  27.             loss,metric = train_step(model,features,labels)
  28.         if epoch%100==0:
  29.             printbar()
  30.             tf.print("epoch =",epoch,"loss = ",loss, "accuracy = ", metric)
  33. train_model(model,epochs = 600)
  1. ================================================================================16:47:35
  2. epoch = 100 loss =  0.567795336 accuracy =  0.71
  3. ================================================================================16:47:39
  4. epoch = 200 loss =  0.50955683 accuracy =  0.77
  5. ================================================================================16:47:43
  6. epoch = 300 loss =  0.421476126 accuracy =  0.84
  7. ================================================================================16:47:47
  8. epoch = 400 loss =  0.330618203 accuracy =  0.9
  9. ================================================================================16:47:51
  10. epoch = 500 loss =  0.308296859 accuracy =  0.89
  11. ================================================================================16:47:55
  12. epoch = 600 loss =  0.279367268 accuracy =  0.96
  1. # 结果可视化
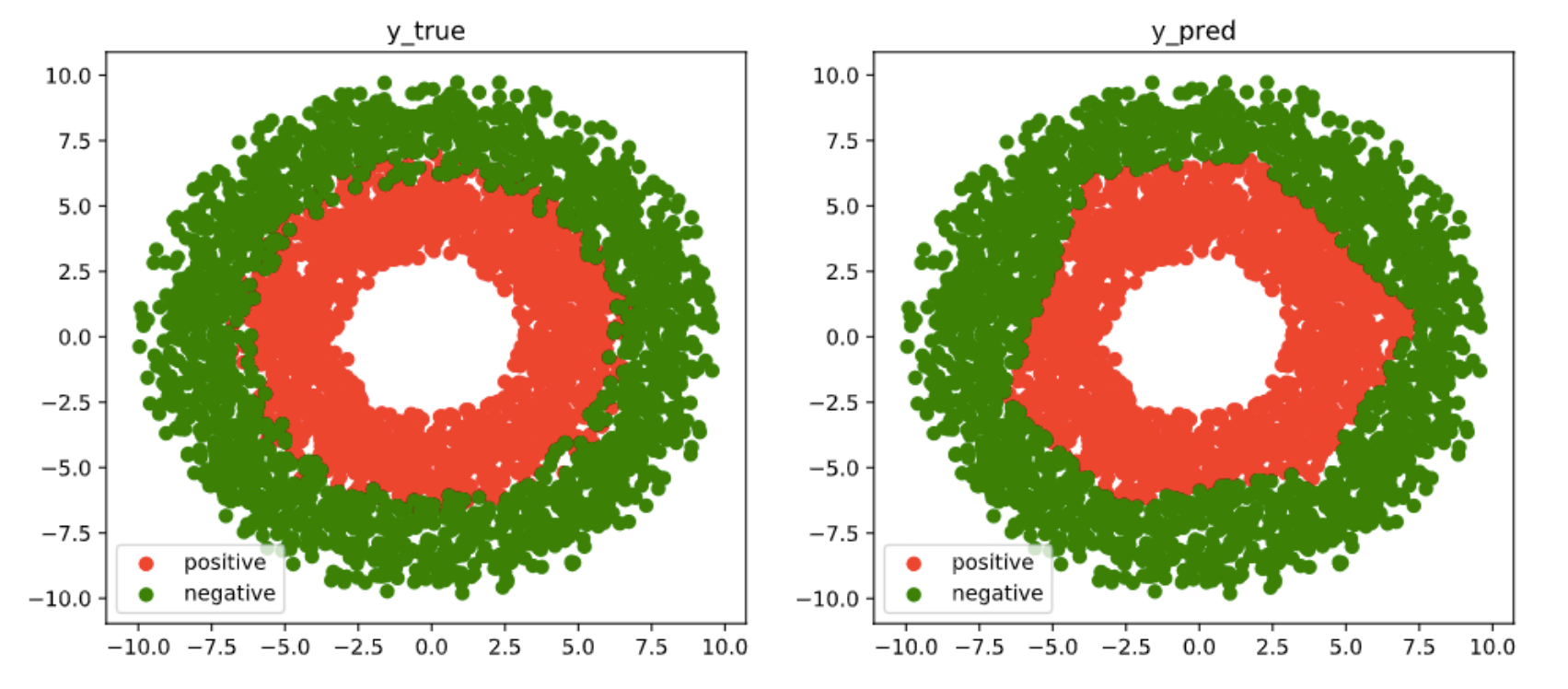
  2. fig, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize = (12,5))
  3. ax1.scatter(Xp[:,0],Xp[:,1],c = "r")
  4. ax1.scatter(Xn[:,0],Xn[:,1],c = "g")
  5. ax1.legend(["positive","negative"]);
  6. ax1.set_title("y_true");
  8. Xp_pred = tf.boolean_mask(X,tf.squeeze(model(X)>=0.5),axis = 0)
  9. Xn_pred = tf.boolean_mask(X,tf.squeeze(model(X)<0.5),axis = 0)
  11. ax2.scatter(Xp_pred[:,0],Xp_pred[:,1],c = "r")
  12. ax2.scatter(Xn_pred[:,0],Xn_pred[:,1],c = "g")
  13. ax2.legend(["positive","negative"]);
  14. ax2.set_title("y_pred");

image.png