2. 反函数的存在性

2.1 单射没有反函数

简而言之：己方与彼方，一个窟窿一个洞。如果对方多了一个或多个小洞时

此时：逆矩阵不存在。

映射是“单”的，即每一个至多有一个与之对应，此时逆矩阵不一定存在。

2.2 满射没有反函数

映射是“满”的。即每一个至少有一个与之对应，此时逆矩阵也不一定存在。

2.3 双射才有反函数

3. 逆矩阵 GOT 1 Question

Q1：逆矩阵为何时 “唯一？”

代数证明如下：（不太理解）

4. 初等变换求逆矩阵 GOT 1 Question

Q1：所有矩阵经过初等行变换一定可以变成单位阵吗？

例：

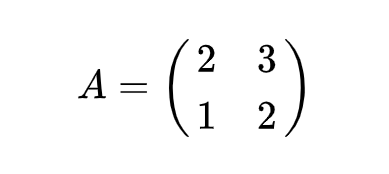
                                           ![image.png](https://cdn.nlark.com/yuque/0/2019/png/348465/1562296579917-8c822557-975a-4323-8d62-fa3ca00c43c2.png#align=left&display=inline&height=155&name=image.png&originHeight=174&originWidth=389&size=8623&status=done&width=345.77777777777777)