1. Markov Model
    2. Hidden Markov Model
      • HMM: Evaluation
      • HMM: Decoding
      • HMM: Learning
    3. Maximum-entropy Markov Model
    4. Conditional Random Fields

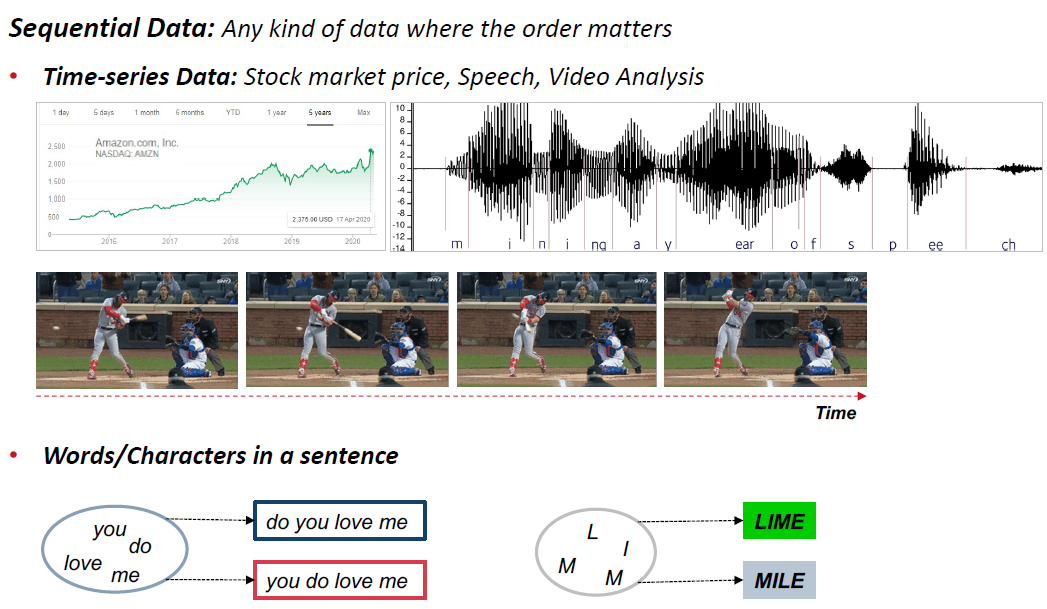
    image.png
    What is the Markov Model? Markov models are used to model chaining systems (Markov Chain)
    一个模型告诉我们一些关于随机变量序列的概率，状态，每个状态都可以从某个集合中取值。
    •假设
    “如果我们想按顺序预测未来，最重要的是当前的状态。在当前状态之前的状态除了通过当前状态对未来没有影响”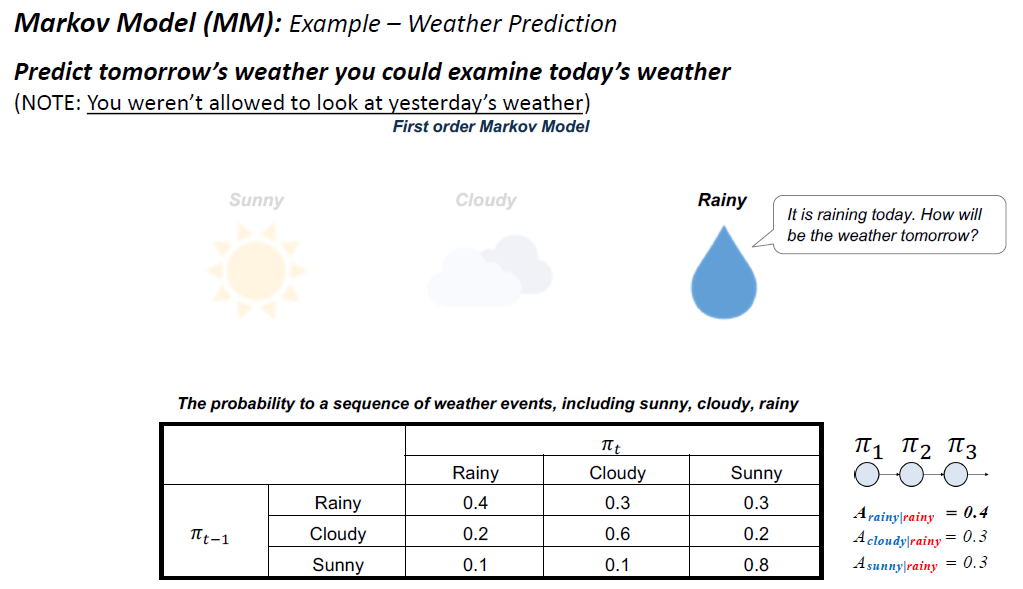
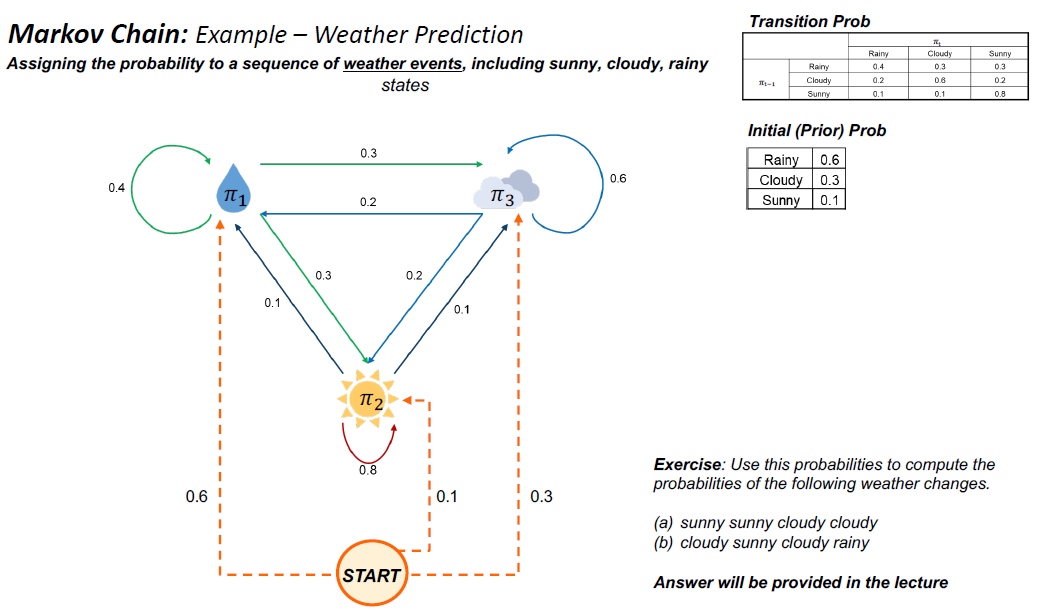
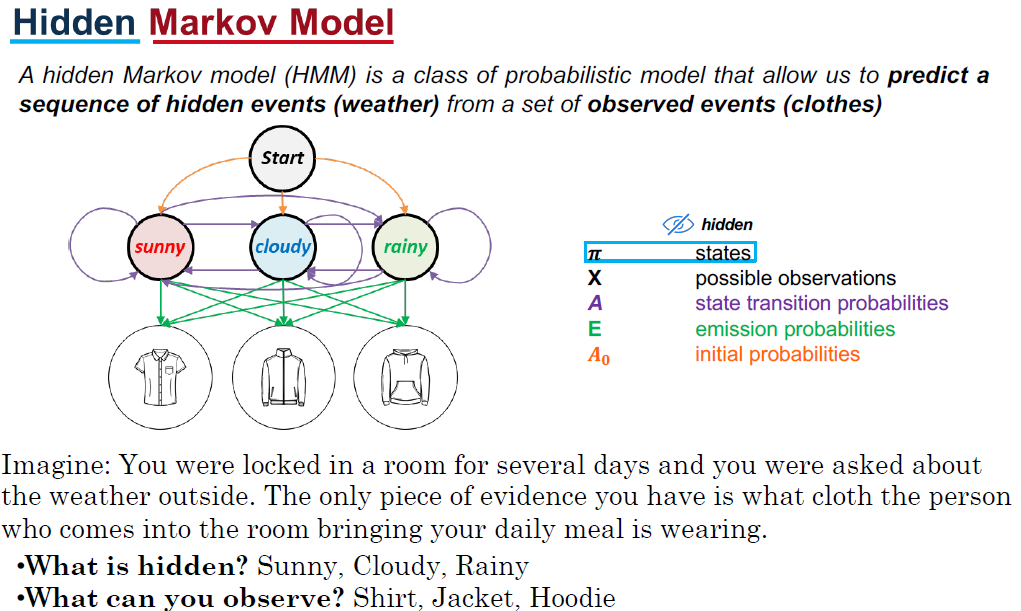
    image.png

    image.pngimage.png
    HMM三个主要问题：
    评价
    •观察到的序列的概率是多少?
    1。计算天气条件“cloud -cloud -sunny”(随机选择)1. 计算一下那个人穿那件衣服的概率
    (天气情况为“多云-多云-晴朗”)
    P (t恤|多云) P(连帽衫|多云) P(连帽衫|阳光)
    2. 计算天气是“多云-多云-晴朗”的概率
    P(sunny|cloudy) P(sunny|cloudy)
    P(t恤|多云)P(帽衫|多云)P(帽衫|晴天)P(多云|多云)P(晴天|多云)
    当我们假设天气(多云-多云-晴朗)时，这只是一个概率。
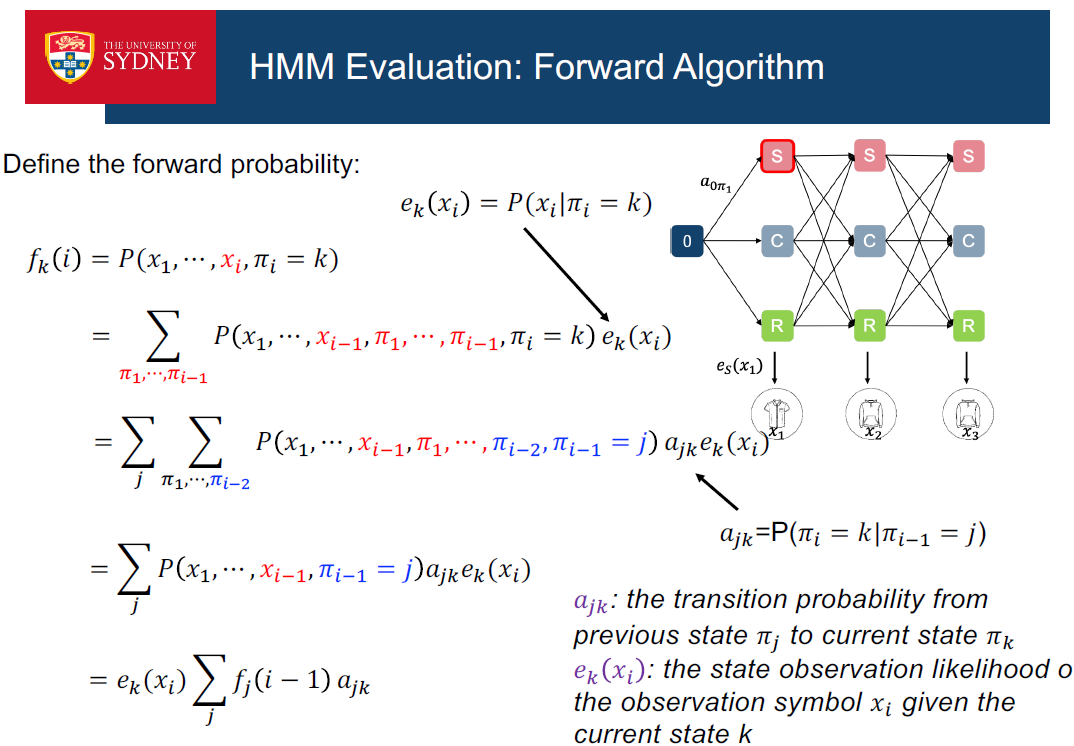
    image.pngimage.pngimage.png
    image.png
    解码
    •给定一个模型和一系列观察结果，最可能的观察状态是什么?
    hmm最常用的算法是维特比算法。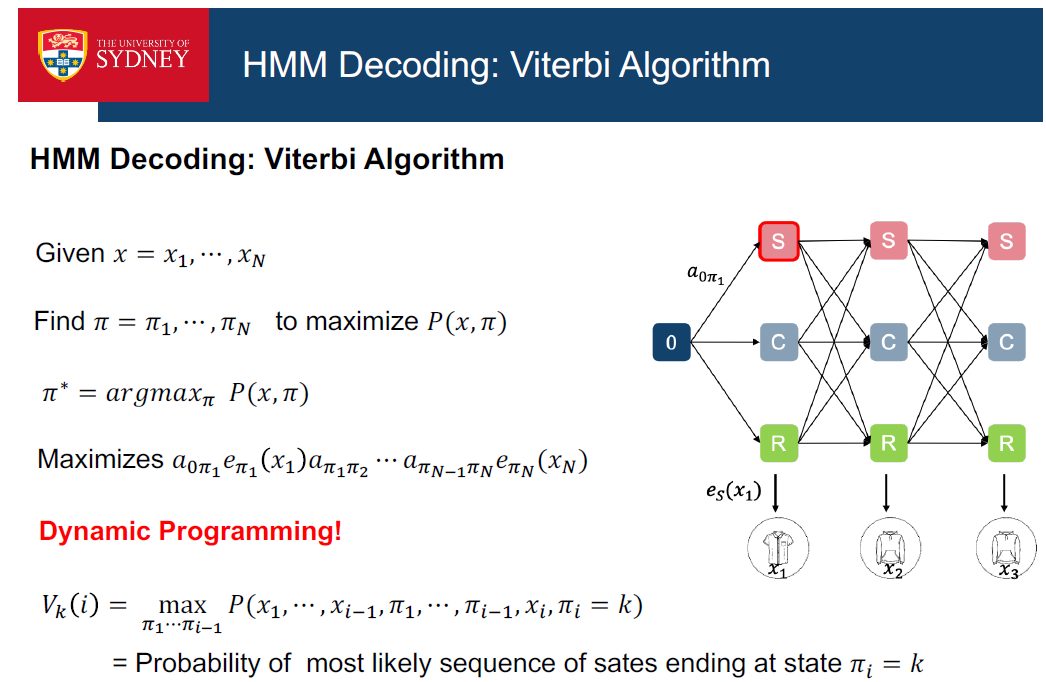
    image.pngimage.pngimage.pngimage.png
    image.png
    学习
    •在什么参数化下观察到的序列是最可能的?
    image.pngimage.pngimage.pngimage.pngimage.pngimage.png
    Maximum-entropy Markov Model
    MEMM考虑了相邻状态和整个观察序列之间的依赖关系，因此具有更好的表达能力。MEMM不考虑P(X)，减少了建模工作量，学习了目标和估计函数之间的一致性。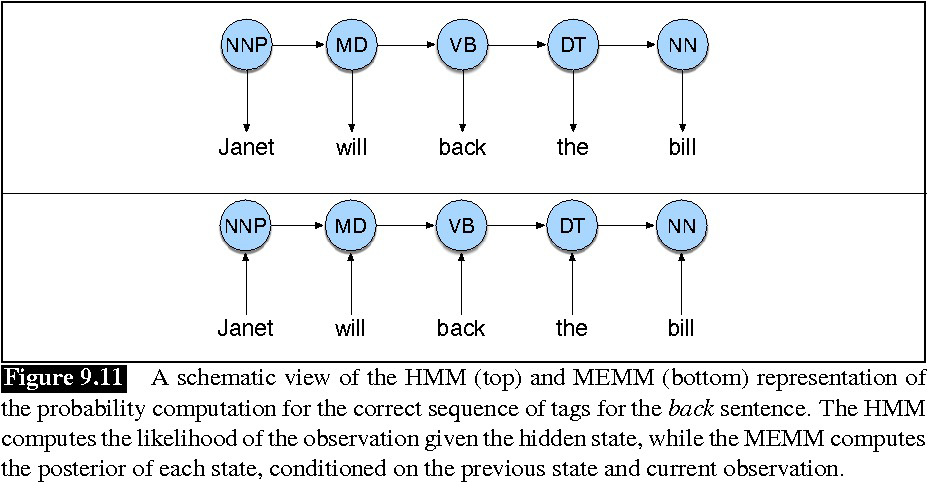image.png
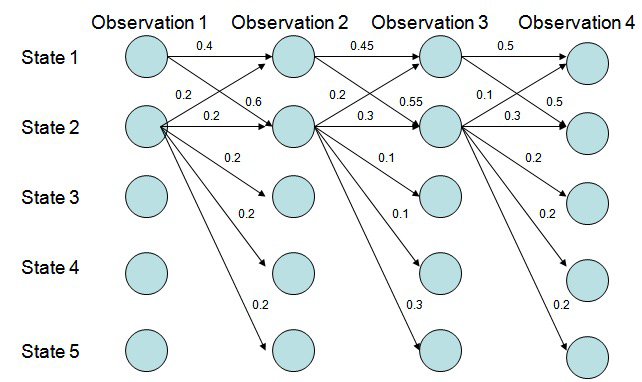
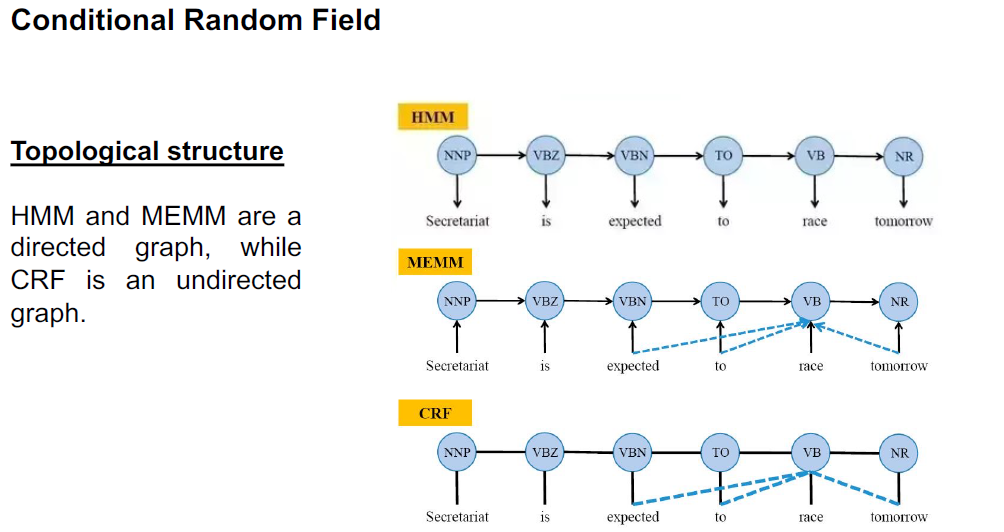
    相对于其他状态，更倾向于具有较少过渡数的状态image.png
    image.png
    Conditional Random Field
    全局最优或局部最优。HMM直接模拟跃迁概率和发射概率，并计算共现概率。
    MEMM基于跃迁概率和发射概率建立共现概率。它计算条件概率，只采用局部方差归一化，容易陷入局部最优。
    CRF在全局范围内计算归一化概率，而不是像MEMM那样在局部范围内计算。它是一个最优全局解，解决了标签问题
    优点：
    •与HMM相比:由于CRF没有像HMM那样严格的独立假设，它可以容纳任何上下文信息。
    •与MEMM相比:由于CRF计算全局最优输出节点的条件概率，它克服了MEMM中标签偏向的缺点。
    但是在算法的训练阶段，CRF具有很高的计算复杂度。这使得当更新的数据可用时，重新训练模型变得非常困难。
    image.pngimage.pngimage.png
    Sample question： The diagram below shows the hidden Markov model for this scenario:Given a sequence of observations (type of clothing), find the hidden sequence of weather states (Sunny or Cloudy) which caused Anna to choose the clothes she wore.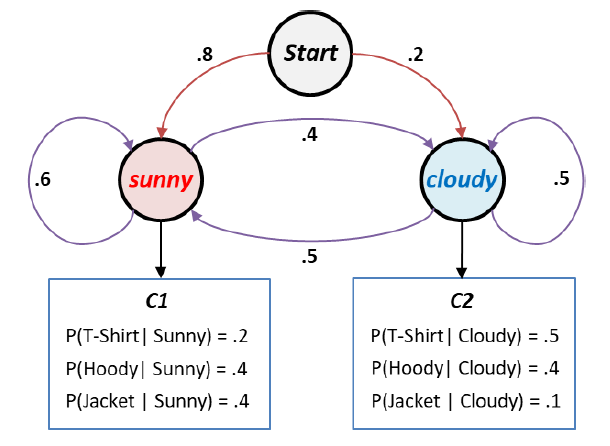
    image.png
    Suppose that you know Anna wore T-shirt on the first day, Hoodie on the second and Jacket on the third day. You know that the weather state of the first day (when Anna wore T-shirt) was Sunny but you do not know the weather states of the next two days.
    a) What is the most likely weather sequence for the three days? Briefly show your calculations. (new
    question)
    Viterbi algorithmn:
    Vs(1) =1 Vc(1) =0 Vr(1) =0
    Vs(2) = es(2)    ass1 =0.40.61= 0.24
    Vc(2) = ec(2)    asc1 =0.40.41== 0.16
    Vs(3) = es(3)    max(Vs(2)ass,Vc(2) acs) =0.40.144 = 0.0576
    Vc(3) = ec(3)    max(Vs(2)asc,Vc(2) acc) =0.1*0.096= 0.0096

    b) What is the probability for a weather sequence Sunny-Cloudy-Sunny for the three days? Briefly
    show your calculations.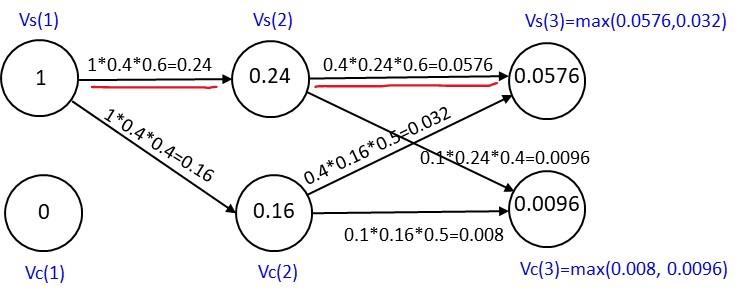
    image.png
    Possible whether seuqneces:
    P(X1=Tshirt,X2 =Hoodie,X3 =Jacket, pie1 =sunny, pie2=cloudy, pie3= sunny) = 0.40.160.5=0.032