• Maximum margin hyperplane
    • Linear SVM
    • Non-linear SVM

    支持向量是是最接近决策边界的例子（数据点）；它们是 被圈起来了
    边缘 -边界 和最接近的 例子之间的间隔
    边界在边缘的中间位置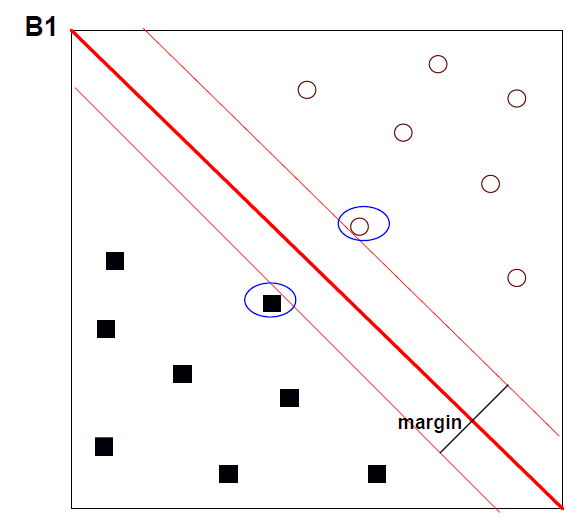
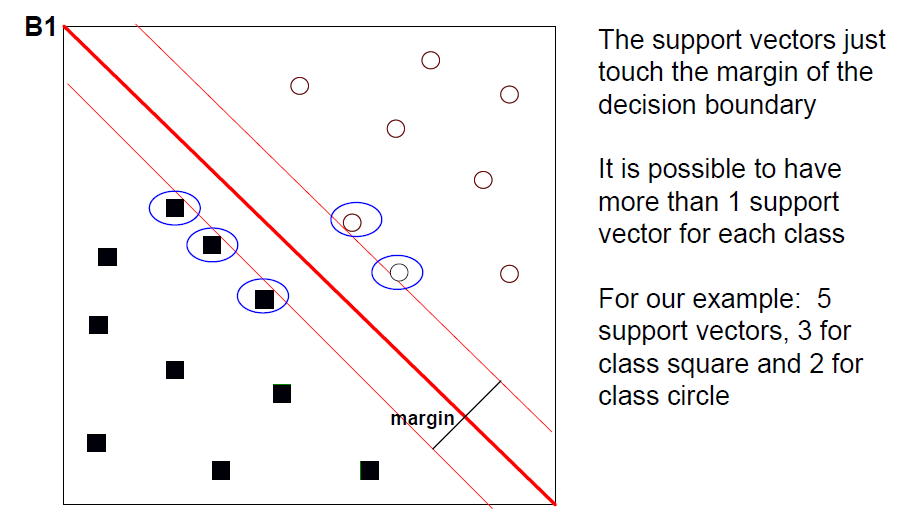
    image.png
    image.png
    image.png
    image.png

    • 具有最大边缘的超平面被称为最大边缘超平面
    • 它是与训练实例的距离可能最大的超平面。
    • SVM选择最大边缘的超平面
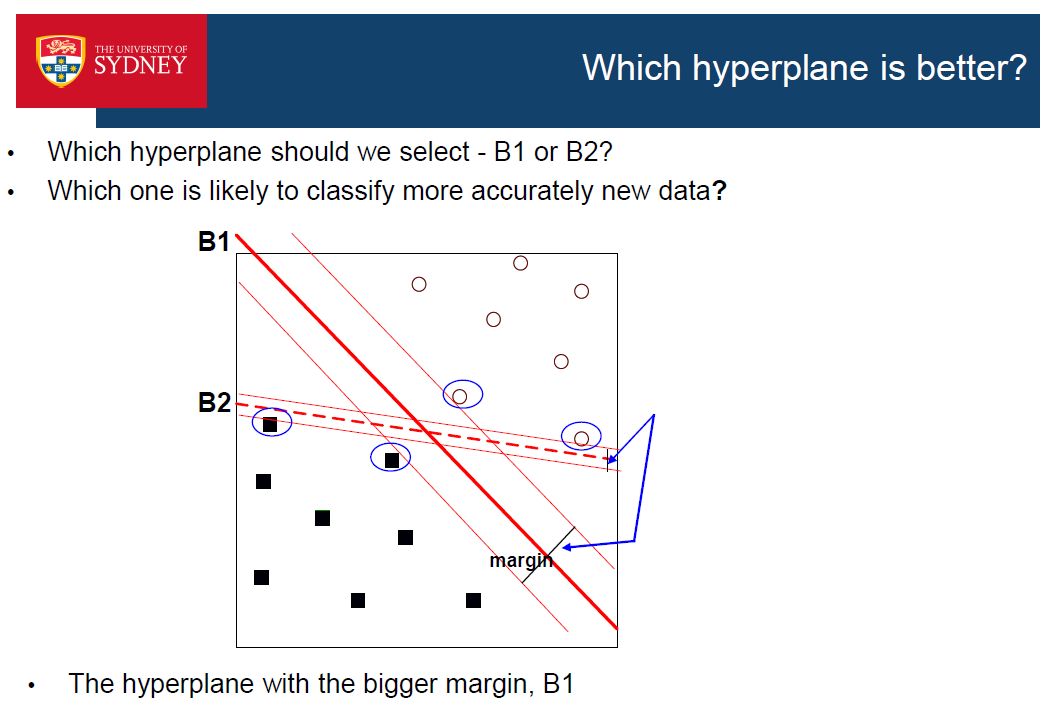
    • 具有大边缘的决策边界（即离训练数据最远的地方）比具有小边缘的决策边界要好，因为它们离训练数据最远。训练数据最远的）比那些小边际的要好，因为它们通常在新的例子上更准确。通常在新的例子上更准确

    Maximum margin hyperplane - rationale
    •如果边界很小，那么超平面或训练示例边界上的任何轻微变化都更可能影响分类，因为允许数据扰动的空间非常狭窄
    •=>小裕度更容易过拟合
    •另一方面，如果利润很大，就有更多的余地对数据的微小变化保持稳健
    •=>可能具有更好的泛化性能
    •统计学习理论也有其合理性，即所谓的结构风险最小化原则
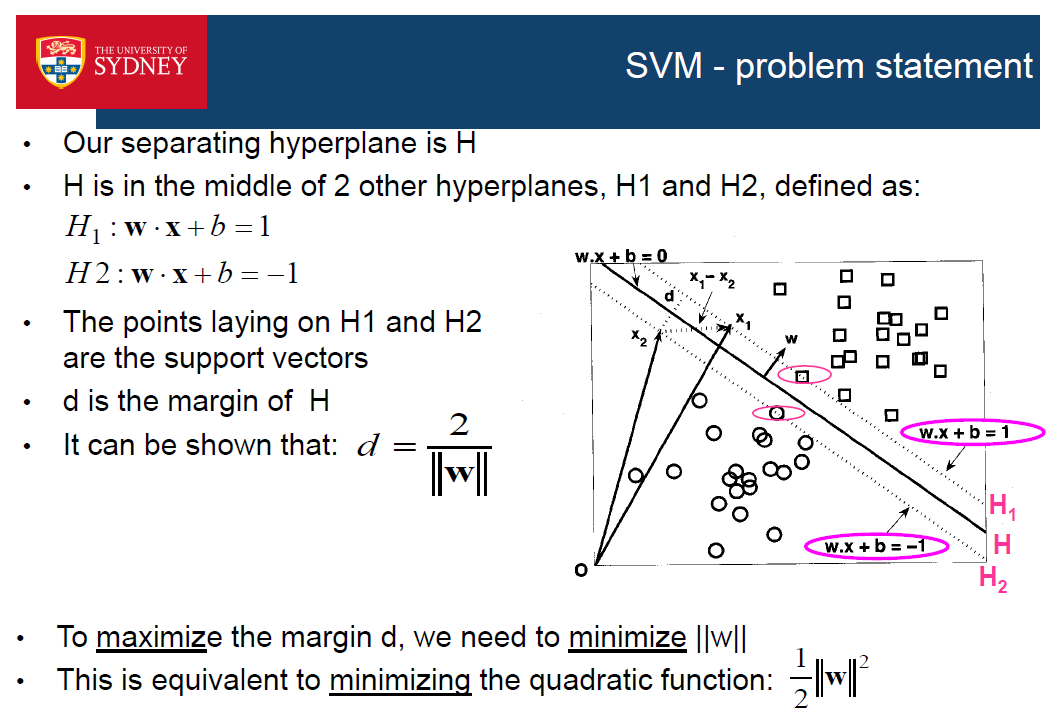
    image.png
    image.png
    image.png
    image.png
    image.png
    这是一个优化问题，可以解决二次规划(QP)和拉格朗日乘子法
    首先，利用拉格朗日乘子lamda将问题转化为等价形式

    Properties of the solution
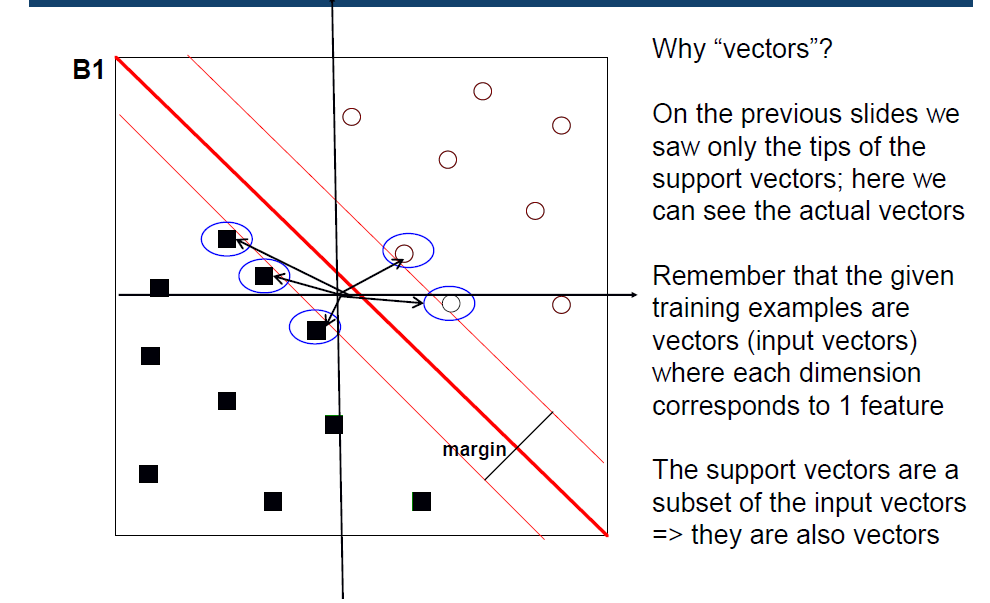
    •最优决策边界(最大边缘超平面)w是训练例的线性组合(系数lamda目标值训练向量)
    •但许多lamda s是0->少量训练示例的线性组合
    •具有非零lamdai的训练例xi为支持向量，它们是最接近决策边界w的例子
    •=>最优决策边界w是支持向量的线性组合
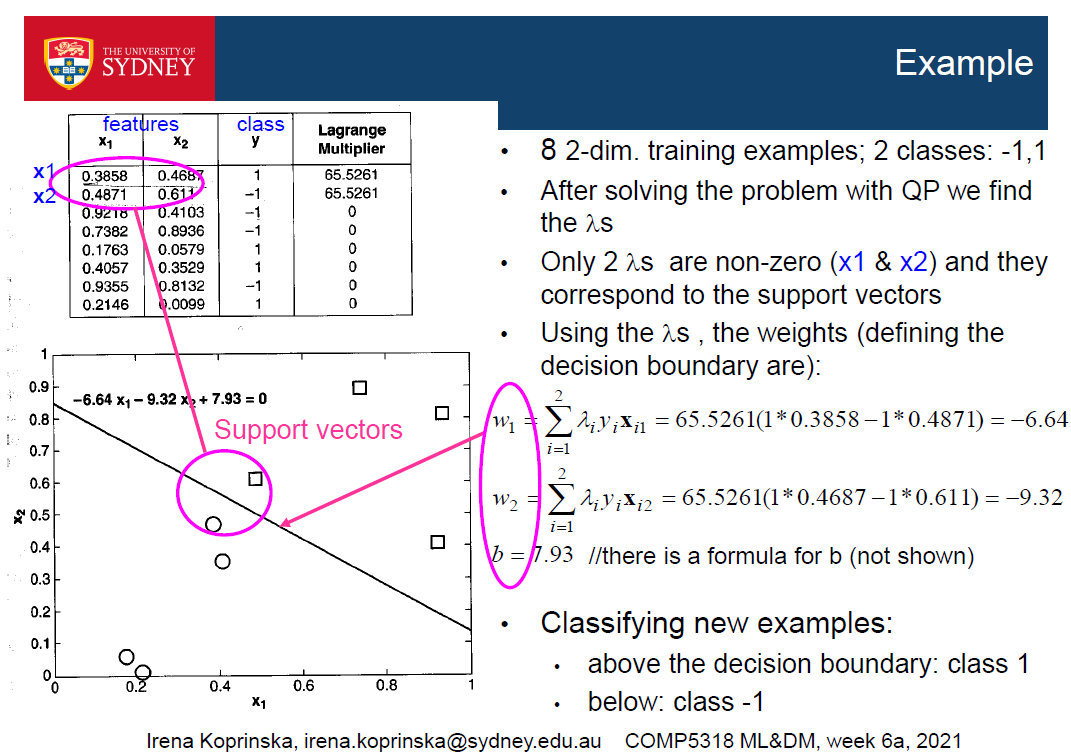
    image.png
    image.png
    •我们目前讨论的方法构建的决策边界是自由的误分类。我们可以允许一些错误的分类。
    •例:B1比B2好，因为它的边缘更大，但现在有两个新的例子补充说;B1对它们分类错误，但B2仍然正确分类
    image.png
    Solutions
    •优化问题的公式类似，但在优化函数的定义中有一个额外的参数C
    •C是一个超参数，允许最大化边缘和最小化训练错误之间的权衡
    •大C:更强调最小化训练误差而不是最大化边缘
    Non-linear SVM
    •在实践中，大多数问题都是线性不可分的
    •支持向量机可以进一步扩展到寻找非线性边界
    Non-linear SVM - Idea
    •将数据从原来的特征空间转换到一个新的空间，在这个空间中可以使用线性边界来分离数据
    •如果转换是非线性的，并且到一个更高的维度空间，它更有可能在其中找到一个线性的决策边界
    •在新的特征空间中学习到的线性决策边界被映射回原特征空间，从而在原空间中形成非线性的决策边界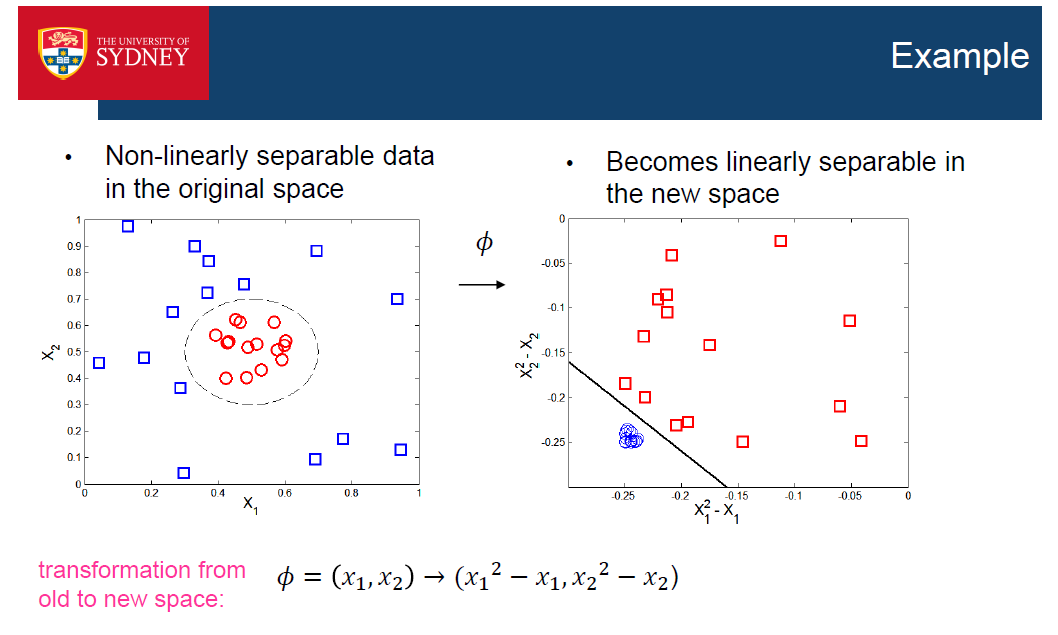
    image.png
    Learning non-linear SVM
    •我们应该使用什么样的映射函数fi?
    •即使我们知道fi，我们如何在新的空间中高效地进行计算?
    •新空间通常具有更高的维度
    •计算高维空间中向量的点积在计算上是昂贵的
    •回想一下，为了找到决策边界，我们计算输入向量的点积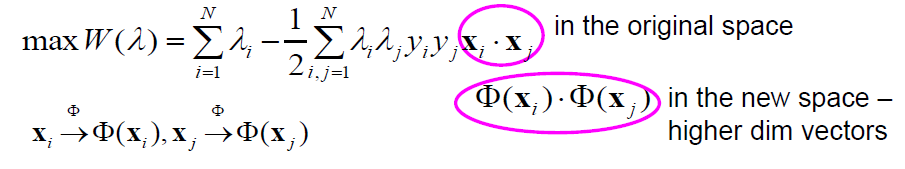
    image.png
    •如何在高维空间中有效计算点积?
    •解决方案:内核技巧
    •计算新空间中一对向量的点积的方法，而不先计算每个向量从原空间到新空间的变换
    •我们需要新空间中特征的点积:
    •我们不会先在新的空间中变换特征，然后再计算它们的点积
    •我们将计算原始特征的点积，并在一个函数(称为核函数)中使用它来确定变换特征的点积
    •核函数指定了原式和反式的点积之间的关系
    image.png
    •我们的例子的内核函数: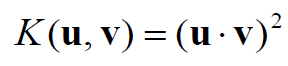image.png
    •核函数允许计算新空间中的点积，而不需要为每个输入向量先计算fi
    •当它们指定了原特征空间和新特征空间的点积之间的关系时，我们可以在原空间中计算一个点积函数，并用它来计算新特征空间中的点积
    •因此，我们通过计算低维空间的核函数来学习高维空间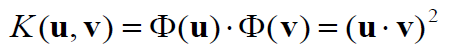image.png
    image.png
    image.png
    image.png
    image.png
    SVM – summary
    •非常流行的分类方法
    •可以形成任意的决策边界(包括线性和非线性)
    •三个关键概念:
    •决策边界是最大边界超平面-该任务被表述为一个优化问题
    •将数据转换为一个新的(通常是高维空间)，在那里它更有可能是线性可分的
    •核技巧——在原始空间中进行计算，而不是在新的高维空间中
    •也可用于多类分类问题-它们被转化为2类问题
    •有一个回归的扩展- Support Vector Regression
    •核化可以应用于所有的算法，可以重新制定，只要用点积计算-一旦这是做点积被替换为核函数，例如k-最近邻和其他

    • Motivation
    • Principal component analysis (PCA)
    • Singular value decomposition
    • Examples
    • PCA for feature extraction
    • PCA for compression

    Motivation
    •一些ML问题涉及数千个特性
    •高维数据的问题
    •较慢的训练
    •不可靠的分类——例子之间距离太远;高维数据是非常稀疏的
    •高维数据更可能出现过拟合
    •构建可解释的模型是不可能的——我们想构建紧凑且易于解释的分类模型
    •可视化——人类只能解释低维数据，例如max三维
    •不是所有的功能都很重要-最好是找到一个更小的功能集，它对于良好的分类来说是必要和充分的特征
    •降维去除冗余和高度相关特征和减少数据中的噪声
    PCA
    •主成分分析(PCA)是最流行的降维方法
    •它通常被称为特征投影法
    •主要的想法是找到一组新的尺寸(轴)和投影数据数据到它上面
    •新空间的维度小于原始空间的维度
    •新的轴捕捉数据的本质(数据的变化)
    •结果数据集(投影)可以作为输入来训练ML算法
    •综上所述，我们构建了新的功能;新特性的数量是比原特性的数量要少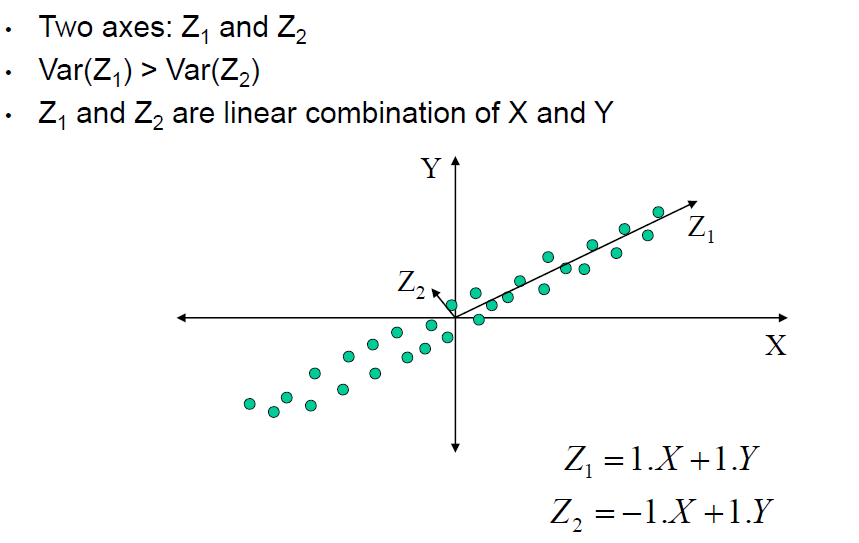
    image.png
    PCA can used for not only vector, but any dimension of input matrix.And PCA only keep subset of the input dimension.
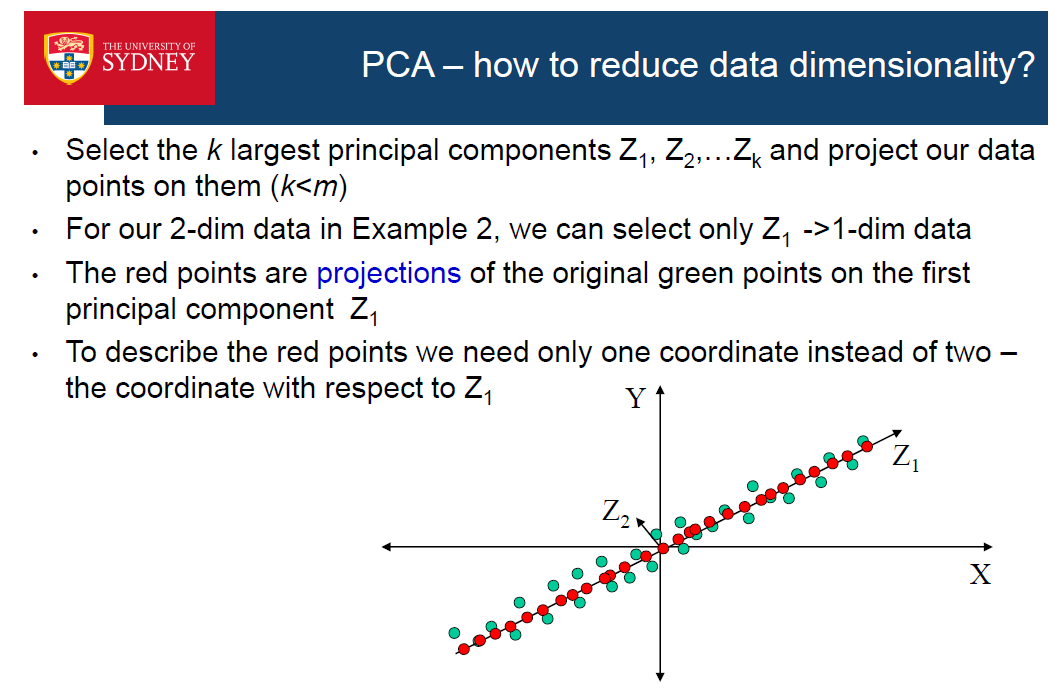
    image.png
    image.png
    image.png
    •我们可以使用新的特征来训练分类器(k最近邻，NB等)如果新的表示更好的话，准确率甚至会提高
    •=>这是一个应用PCA的特征提取-找到一个更低维的表示，比原来的表示更适合
    How to find the principal components?奇异值分解
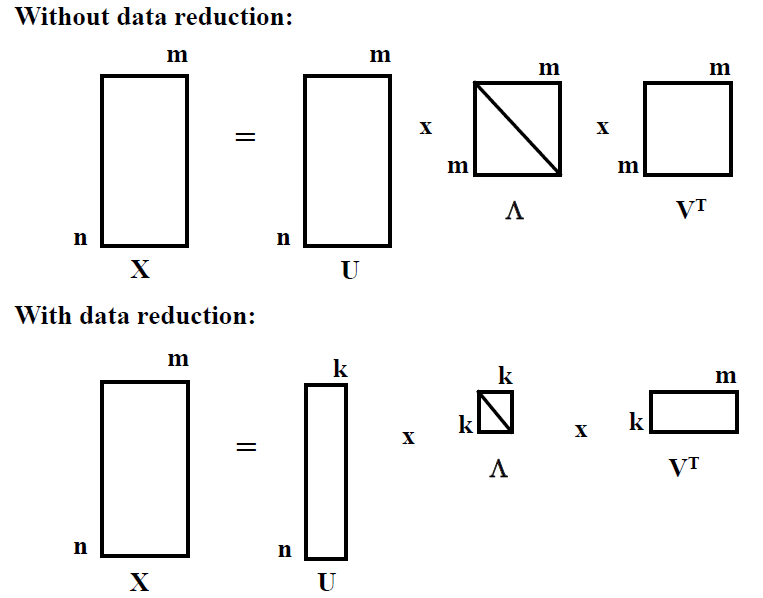
    image.png
    image.png
    image.png
    image.png
    image.png
    image.png
    Summary
    •PCA是一种降维方法
    •这是一个非监督方法-它不使用类信息
    •它将数据投射到一个更低维度的空间中，仍然能够捕捉到重要的信息
    •新的坐标轴是根据他们捕获的方差排序的
    •第一个轴指向数据中方差最大的方向
    •第二个轴与第一个轴正交，并朝着方差第二高的方向，以此类推
    •新的坐标轴称为主分量，表示数据中的模式
    •数据维数降低