什么情况用动态规划

  • 发现有重叠子问题的

动态规划阶梯套路

  • 写出动态状态转移方程

题目：求一组数字不相邻的数字和最大值

例如：3 3 4 1 9 3 6 6，最大值是 22

分析

求解动态规划的套路是把每一种情况都分为两种选择，要么选，要么不选。例如在 8 个数中求不相邻和的最大值，例如你选了序号8，就不能选7了。每一位就有两种情况，要么选，要么不选。拿序号8来说：
image.png
如果选：也就是如果选 8，那么最优解可能是 8 本身的值 6，加上左边 6 个数中的其中一个，7 不能选了。所以得出等式为：opt(8) = opt(6) + 6。

如果不选：不选的话就是从左边的7个中选两个，换句话说就是从 7 个数中求两和的最大值。所以可以得出等式为：opt(8) = opt(7)。

这里的 opt 是单词 optimal（最优）的缩写。

对于上面一位数字是这么分析的，其它的 7 位也是这样分析，每一位有两种情况，我们只要比较出这两种情况中最大的那个值就可以了。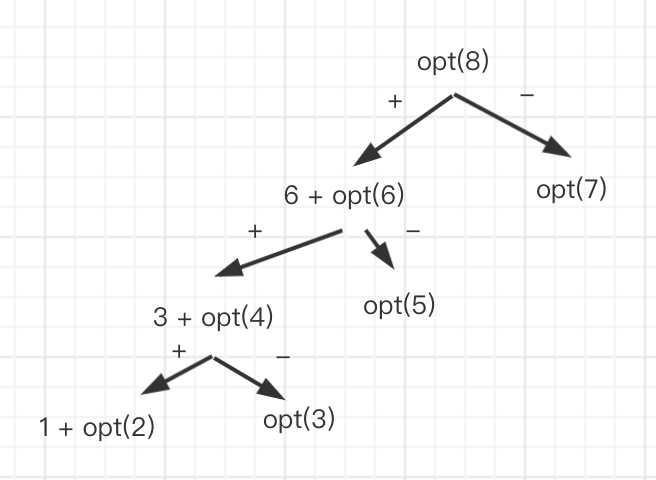
image.png
(+表示选，-表示不选)
所以得出动态转移方程为：
选：opt(n) = opt(n-2) + arr[n-1]
不选：opt(n) = opt(n)

递归的出口：
当 n = 1 那么只能是 n 本身了；if (n == 1) return arr[n-1];
当 n = 2 那么可能是 1，或者是 2；if(n == 2) retur max(arr[n-1],arr[n-2])

递归求解

先尝试用递归的方式写：

  2. /**
  3.  * @description:
  4.  * 在一组数中，求不相邻之间的数最大和是多少
  5.  * 例如：
  6.  * 3 3 4 1 9 3 6 6
  7.  * 最大值是 22
  8.  * @date: 2020-06-16 02:32
  9.  * @author: 十一
  10.  */
  11. public class Sum {
  13.     @Test
  14.     public void testRecOpt() {
  15.         int[] arr = {3,3,4,1,9,3,6,6};
  16.         int i = arr.length;
  17.         Sum sum = new Sum();
  18.         int r = sum.recOpt(i, arr);
  19.         System.out.println(r);
  20.         Assert.assertEquals(22,r);
  22.         int[] arr2 = {1,2,4,1,7,8,3};
  23.         int i2 = arr2.length;
  24.         r = sum.recOpt(i2, arr2);
  25.         System.out.println(r);
  26.         Assert.assertEquals(15,r);
  27.     }
  29.     /**
  30.      * 递归求最优解
  31.      * @param i      序号 - 1 = 数组下标
  32.      * @param arr    数组
  33.      * @return
  34.      */
  35.     public int recOpt(int i,int[] arr) {
  36.         // 1. 递归先写退出条件
  37.         if (i == 1) {
  38.             return arr[i - 1];
  39.         }
  40.         if (i == 2) {
  41.             return max(arr[i - 1], arr[i - 2]);
  42.         }
  43.         // 2. 选，就是左边隔一个的最优解 + 自己
  44.         int a = recOpt(i - 2,arr) + arr[i - 1];
  45.         // 3. 不选，就是左边的最优解
  46.         int b = recOpt(i-1,arr);
  47.         return max(a,b);
  48.     }
  50.     public int max(int a,int b) {
  51.         return a > b ? a : b;
  52.     }
  53. }

缺点：递归会重复的计算一些已经算过的，非常浪费！

动态规划求解

动态规划求解不会有很多重复，是因为用一个内存空间来保存了每个节点的值，也是空间换时间。

  1. @Test
  2. public void testDpOpt() {
  3.     int[] arr = {3,3,4,1,9,3,6,6};
  4.     Sum sum = new Sum();
  5.     int r = sum.dpOpt(arr);
  6.     System.out.println(r);
  7.     Assert.assertEquals(22,r);
  9.     int[] arr2 = {1,2,4,1,7,8,3};
  10.     r = sum.dpOpt(arr2);
  11.     System.out.println(r);
  12.     Assert.assertEquals(15,r);
  13. }
  14. public int dpOpt(int[] arr) {
  15.     // 保存每种情况的值
  16.     int opt[] = new int[arr.length];
  17.     // 这两种情况是已知的
  18.     opt[0] = arr[0];
  19.     opt[1] = max(arr[0],arr[1]);
  21.     for (int i = 2; i < arr.length; i++) {
  22.         int a = opt[i - 2] + arr[i];
  23.         int b = opt[i - 1];
  24.         opt[i] = max(a,b);
  25.     }
  26.     return opt[arr.length -1];
  28. }
  29. public int max(int a,int b) {
  30.     return a > b ? a : b;
  31. }

题目：机器人走方格

有一个 m * n 的网格，机器人一次只能走一个格点，且只能向右或向下走，要从左上角走到右下角。请设计一个算法，计算机器人有多少种走法。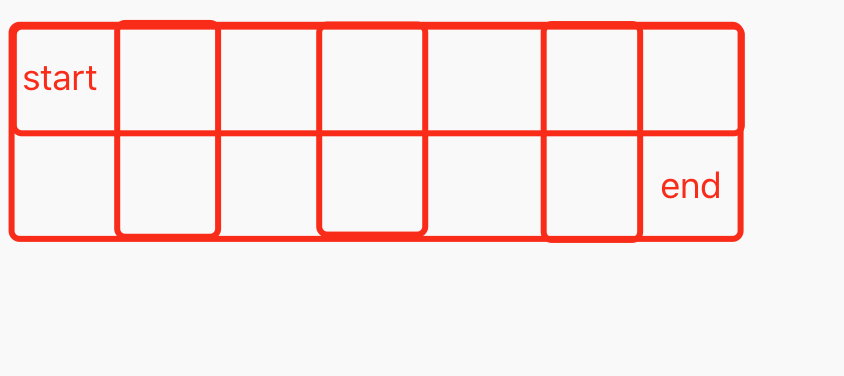
image.png

分析

机器人要么往下走，要么往右走，所以在坐标轴中可以看做，起点是（m，n）终点是（0，0），那么当 m or n = 1 时，这时只能往一个方向走，当 m or n > 1 时，这时对于每一个格子来说都有两种走法，往下或往右。

递归出口为：if(m == 1 || n == 1) return 1;

状态转移方程：f(m,n)=(m-1,n)+(m,n-1);

递归求解

  1. public int f1(int m, int n) {
  2.     if (m == 1 || n == 1) {
  3.         return 1;
  4.     }
  6.     return f1(m-1,n) + f1(m,n-1);
  7. }

动态规划

动态规划和递归类似，这里用数组来保存状态

  1. public int f2(int m, int n) {
  2.     int[][] r = new int[m+1][n+1];
  3.     r[0][0] = 0;
  4.     for (int i = 1; i <= m; i++) {
  5.         for (int i1 = 1; i1 <= n; i1++) {
  6.             if (i1 - 1 == 0 || i - 1 == 0) {
  7.                 r[i][i1] = 1;
  8.                 continue;
  9.             }
  10.             r[i][i1] = r[i-1][i1] + r[i][i1-1];
  11.         }
  12.     }
  13.     return r[m][n];
  14. }