递归

递归就是函数自己调用自己。

递归的技巧

1. 要找到退出条件
2. 要不断的缩小下一次调用的范围，不然就无限了
3. 要让本次的调用过程中的值参与进来，不然本次几乎就没意义了

题目练习

1. 斐波那契

斐波那契数列，求第 n 位是数多少。例如：1 1 2 3 5 8 13 21

题解：
_从第 3 位数开始，它的值是前两位的和；得到方程：_f(n-1) + f(n-2)

1. 退出条件

   if (n <= 2) {
    return n;
   }

2. 缩小下一次调用

   f(n-1) + f(n-2)

   代码：

   public int f(int n) {
    if (n <= 2) {
        return 1;
    }
    return f(n-1) + f(n-2);
   }

   2. 求阶乘

   求 n 的阶乘。例如：4 = 4 x 3 x 2 x 1

题解：
n 的阶乘等于n f( n-1) 的阶乘，得到递归方程：n f(n - 1)

1. 退出条件

   if (n <= 2) {
    return n;
   }

2. 缩小下一次调用

   f(n - 1)

代码：

public int f(int n) {
    if (n <= 2) {
        return n;
    }
    return n * f(n - 1);
}

3. 跳台阶

一次只能是1个或2个台阶，跳到n个有多少种跳法。例如：n=2，有2种

题解：
当 n>=2，那么是一次跳2，或者跳两次1，得到递归的方程 f(n-1)+f(n-2)

1. 退出条件

   if (n <= 2) {
    return n;
   }

2. 缩小下一次调用

   f(n-1) + f(n-2)

   代码：

   public int f(int n) {
    if (n <= 2) {
        return n;
    }
    return f(n-1) + f(n-2);
   }

4. 反转链表

反转单链表。例如链表为：1->2->3->4。反转后为 4->3->2->1
题解：
递归到最后一个把它存下来，然后清空。

1. 退出条件

   if (head == null || head.next == null) {
    return head;
   }

2. 缩小下一次调用

   Node last = reverse(head.next)

   代码： ```java class Node { int data; Node next; }
   public Node reverse(Node head) { if (head == null || head.next == null) {

    return head;

   } // last 是链表最后一个值 Node last = reverse(head.next); // head 会保留最后两个值 Node t1 = head.next; // 追加一个反转节点 t1.next = head; // 将多余的置为null head.next = null; // return last;

}

<a name="7ZaiG"></a>
### 5. 递归乘法
_递归乘法。 写一个递归函数，不使用 * 运算符， 实现两个正整数的相乘。可以使用加号、减号、位移，但要吝啬一些。_
_输入：A = 1, B = 10  输出：10_
分析：例如 3 x 4，可以等于 4 x 4 x 4，也就是递归 3 次
1. 退出条件 B 等于 1
```java
if (B == 1) {
    return A;
}

1. 缩小下一次调用

   return A + f1(A,B -1);

   代码： ```java public int f1(int A,int B) { if (A == 0 || B == 0) {

    return 0;

   } if (B == 1) {

    return A;

   } // 需要保证A大于B，这样减少循环次数 int max; if (A < B) {

    max = B;
    B = A;
    A = max;

   }

   return A + f1(A,B -1);

}

<a name="0ibPH"></a>
## 递归的优化
1. 使用临时变量将结果存起来，下次遇到直接调用
2. 递归一般是都是从上到下开始的，可以考虑从下到上，逆向推导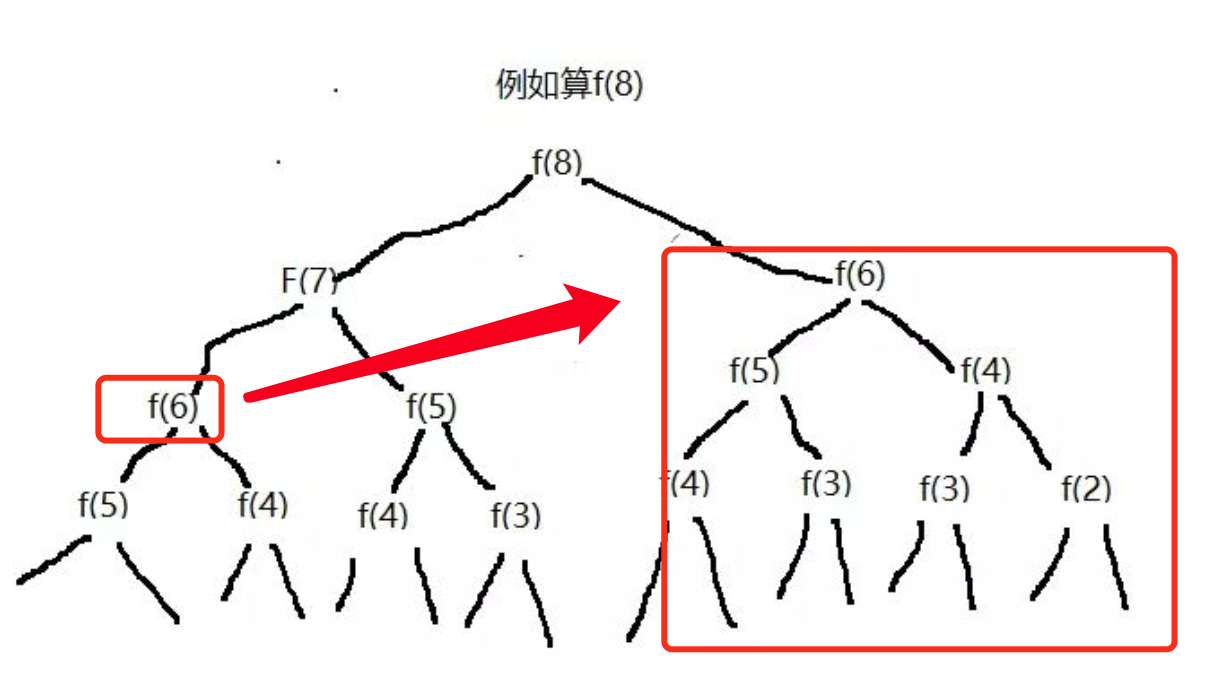
![image.png](https://cdn.nlark.com/yuque/0/2020/png/316467/1592710471394-4ad3c004-73a1-4382-8c4c-e9f9e22a89d6.png#height=338&id=umGAf&margin=%5Bobject%20Object%5D&name=image.png&originHeight=676&originWidth=1218&originalType=binary&ratio=1&size=298528&status=done&style=none&width=609)
<a name="Tu5za"></a>
## 题目练习
<a name="P6cra"></a>
### 1. 斐波那契优化
根据斐波那契的特性，计算某个值，但它前面的两个值以及计算过了，可以存储起来，不需要再重复计算，性能大大提升。时间复杂度从原来的O(2^n)到O(n)。
```java
private static Map<Integer,Integer> indexCacheOfVal = new HashMap<>();
private static int recursionWithCache(int i) {
    if (i <= 1) {
        return i;
    }
    if (indexCacheOfVal.containsKey(i)) {
        return indexCacheOfVal.get(i);
    }
    int v = recursionWithCache(i-1) + recursionWithCache(i-2);
    if (!indexCacheOfVal.containsKey(i)) {
        indexCacheOfVal.put(Integer.valueOf(i),v);
    }
    return v;
}