08_反向传播

反向传播算法是训练神经网络的最常用且最有效的算法. 本节我们将阐述反向传播算法的基本原理, 并用PyTorch框架快速实现该算法.

知识点

• 正向传播算法
• 梯度下降算法
• 反向传播算法

  正向传播

神经网络本质上是一个非常复杂且有大量参数的复合函数,我们将数据作为函数的输入,将结果作为函数的输出.

正向传播算法其实就是通过函数的输入以及神经网络(一个复杂的复合函数), 得到函数的输出的过程.

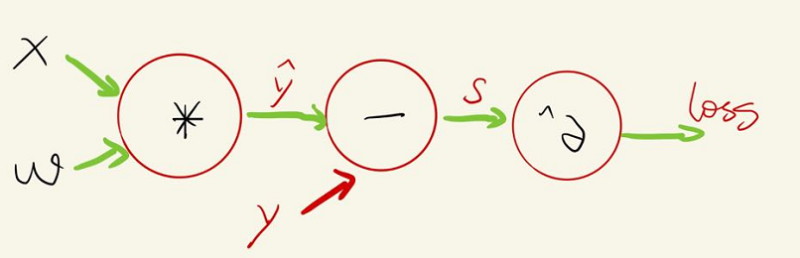
该函数的输入数据为x, 参数为w, 输出为loss

则该函数正向传播过程如下:

上面的步骤就是正向传播的全部过程

import torch
def forward(x, y, w):
    y_predicted = w * x
    loss = (y_predicted - y)**2
    return los
x = torch.tensor(1.0)
y = torch.tensor(2.0)
w = torch.tensor(1.0, requires_grad=True)
forward(x, y, w)

反向传播

反向传播的目的就是计算输出值和参数之间的梯度关系.

在正向传播中,我们的参数w被随机定义为了1. 可以看出,此时的w并不能很好的根据x值预测出y值. 我们需要找到更佳的参数

那么如何获得更佳的参数值呢? 我们一般采用的就说梯度下降法. 该方法将在下一节详细阐述.

参数的偏导数才能使用梯度下降算法,因此反向传播孕育而生.

利用反向传播求取函数关于权重的偏导, 然后根据偏导使用梯度下降算法找到最佳的参数. 这个过程起始就是深度学习中的模型训练的过程.

那么如何利用PyTorch实现反向传播呢?

其实和上一节求取梯度的方法一致,即利用loss.backward()进行反向传播,求取所要偏导变量的偏导值:

x = torch.tensor(1.0)
y = torch.tensor(2.0)
w = torch.tensor(1.0, requires_grad=True)
loss = forward(x, y, w)
loss.backward()
print("此时,loss关于w的偏导值:", w.grad)
w.grad.zero_()

小结

本节我们主要是对loss.backward()进行了详细的讲解.这个函数说所有神经网络模型训练中,都会使用的函数.

注意,在进行反向传播和梯度下降后,记得对梯度进行清空,防止梯度累加.