激活函数

概述

激活函数是机器学习中很重要的一个概念.在神经网络中,我们经常使用线性运算来解决非线性问题.

在生活中大多数问题,都不是简单线性运算.这时,我们就需要用到激活函数来解决非线性的问题. 本节我们主要学习机器学习中常用的激活函数. 利用激活函数,建立一个简单的三层神经网络模型.

知识点:

  • Sigmoid函数
  • ReLU函数
  • Tanh函数

激活函数

激活函数是机器学习中的很重要的概念.在神经网络中,我们经常使用线性运算来解决线性问题. 非线性的问题,我们需要用到激活函数

简单来说,传统的全连接网络是让数据不断的通过线性函数层和激活函数层,进而得到最终的预测结果. 因此, 如果我们学习完激活函数后, 就可以结合之前学过的线性函数来完成一个传统全连接网络模型了.

常见的激活函数有Sigmoid函数,tanh函数Relu函数

Sigmoid函数

sigmoid函数是机器学习中最经典的且最早被使用的激活函数之一.它的公式如下

13_激活函数 - 图1

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. %matplotlib inline
  5. # 手写 sigmoid 函数
  6. def sigmoid(x): return 1 / (1 + np.exp(-x))
  8. # 画图
  9. y = np.linspace(-10, 10, 100)
  10. plt.plot(y, sigmoid(y), 'b')
  11. plt.grid(linestyle='--')
  12. plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
  13. plt.yticks([0, 0.5, 1])
  14. plt.ylim(0, 1)
  15. plt.xlim(-4, 4)
  16. plt.show()

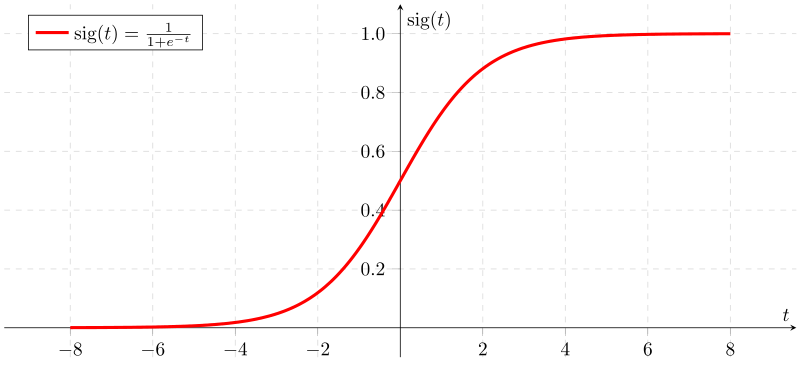
13_激活函数 - 图213_激活函数 - 图3

从图中可以看到,激活函数Sigmoid在定义域内处处可求导. 但是,通过曲线的斜率,可以发现,当输入一个较小或较大的数据时,该函数的导数会变得很小,梯度趋近于0. 例如, 每一次梯度值都减少0.25,如果神经网络层级过多,那么当梯度穿过多层后将变得非常接近于0,如0.03的n次方. 即出现梯度消失的现象,进而造成模型无法收敛. 这也就是曾经被广泛使用的sigmoid函数,现在却很少使用的原因

除了自定义sigmoid函数之后,我们还可以直接使用pytorch提供的

  1. import torch
  2. import torch.nn as nn
  3. import torch.nn.functional as F
  5. # pytorch 中有两种实现方法
  6. x = torch.tensor([-1.0, 1.0, 2.0, 3.0])
  7. output = torch.sigmoid(x)
  8. print(output)
  9. s = nn.Sigmoid()
  10. output = s(x)
  11. print(output)

Tanh函数

Tanh是双曲函数中的双曲正切函数.在数学中, 双曲正切函数都是由双曲正弦函数和双曲余弦函数推导而来. 函数的具体形式如下:

13_激活函数 - 图4%20%3D%20%5Cfrac%7Be%5Ex%20-%20e%5E%7B-x%7D%7D%7Be%5Ex%20%2B%20e%5E%7B-x%7D%7D%0A#card=math&code=tanh%28x%29%20%3D%20%5Cfrac%7Be%5Ex%20-%20e%5E%7B-x%7D%7D%7Be%5Ex%20%2B%20e%5E%7B-x%7D%7D%0A&id=rLrGW)

Tanh的函数图像如下:

  1. def tanh(x): return 2*sigmoid(2*x)-1
  4. y = np.linspace(-10, 10, 100)
  5. plt.plot(y, tanh(y), 'b')
  6. plt.grid(linestyle='--')
  7. plt.xlabel('X Axis')
  8. plt.ylabel('Y Axis')
  9. plt.xticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
  10. plt.yticks([-1, 0, 1])
  11. plt.ylim(-1, 1)
  12. plt.xlim(-4, 4)
  13. plt.show()

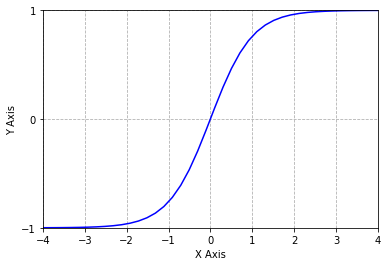
13_激活函数 - 图5
13_激活函数 - 图6

从上图可以看出,双曲正切函数和Sigmoid函数图像很想,但是tanh函数的范围是(-1,1), 而Sigmoid函数的范围为(0,1)

同Sigmoid类似,PyTorch中也实现了tanh

  1. output = torch.tanh(x)
  2. print(output)
  3. t = nn.Tanh()
  4. output = t(x)
  5. print(output)

ReLU函数

双曲正切函数和Sigmoid函数相似,都存在梯度消失的现象.且由于解析式中存在幂运算, 计算机需要消耗大量的时间成本. 因此, 为了解决梯度消失的问题, 线性修正单元函数（Rectified Linear Units，简称ReLU）就诞生了.

ReLU函数是目前最常用的激活函数之一

13_激活函数 - 图7%3D%20%5Cbegin%7Bcases%7D%200%26%20%5Ctext%7Bx%20%24%3C%24%200%7D%5C%5C%20x%26%20%5Ctext%7Bx%20%24%5Cgeq%24%200%7D%20%5Cend%7Bcases%7D%0A#card=math&code=f%28x%29%3D%20%5Cbegin%7Bcases%7D%200%26%20%5Ctext%7Bx%20%24%3C%24%200%7D%5C%5C%20x%26%20%5Ctext%7Bx%20%24%5Cgeq%24%200%7D%20%5Cend%7Bcases%7D%0A&id=I9BCj)

其中x为常数.可以看到, 当x < 0 时,ReLU全部取值为0, 梯度也为0,减少了梯度运算的成本. 当 13_激活函数 - 图8时,ReLU的取值为x, 梯度始终为一个固定的值, 进而缓解了梯度消失的问题

  1. def relu(x): return np.where(x >= 0, x, 0)
  4. y = np.linspace(-10, 10, 1000)
  5. plt.plot(y, relu(y), 'b')
  6. plt.grid(linestyle='--')
  8. plt.xticks([-3, -2, -1, 0, 1, 2, 3])
  9. plt.yticks([0, 1, 2, 3])
  10. plt.ylim(0, 3)
  11. plt.xlim(-3, 3)
  12. plt.show()

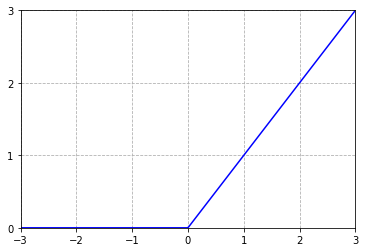
13_激活函数 - 图9
13_激活函数 - 图10

利用PyTorch中的ReLU函数处理输入数据:

  1. output = torch.relu(x)
  2. print(output)
  3. relu = nn.ReLU()
  4. output = relu(x)
  5. print(output)

至此,我们学习完了机器学习中的常见几种激活函数. 当然上一节所学的Softmax函数也算一个激活函数,它主要应用于神经网络模型的最后一层.

如果我们需要解决二分类问题, 我们一般会将最后一层设置为Sigmoid函数层. 因此, 从Sigmoid函数图像可以看出,该函数范围为(0,1) 这样可以很好的表示概率值

综上, 考虑到每种激活函数的特型,我们得到了一下的规则:

  • 如果在神经网络内部(隐藏层)需要使用激活函数,一般会使用ReLU函数或者ReLU函数的改进来进行激活
  • 如果是二分类问题,那么在神经网络最后一层加上Sigmoid函数层
  • 如果是多分类问题,那么会在神经网络最后一层加上Softmax函数层

神经网络的建立

神经网络其实就是很多线性函数和非线性函数组成的复杂函数. 至此, 我们已经学习了线性函数和非线性函数的定义方式. 接下来, 让我们根据这些知识点建立一个完整的神经网络模型.

在利用PyTorch建立神经网络模型时,需要注意以下几点:

  • 自定义的神经网络模型必须继承nn.Module
  • 自定义的类中需要实现__init__和forward函数
  • __init__: 定义网络的结构
  • forward: 定义数据在模型中的传播路径
  1. # 神经网络的建立
  2. class NeuralNet(torch.nn.Module):
  3.     def __init__(self,input_size,hidden_size):
  4.         super(NeuralNet,self).__init__()
  5.         self.linear1 = torch.nn.Linear(input_size,hidden_size)
  6.         self.relu = torch.nn.ReLU()
  7.         self.linear2 = torch.nn.Linear(hidden_size,1)
  8.         self.sigmoid = torch.nn.Sigmoid()
  10.     def forward(self,x):
  11.         out = self.linear1(x)
  12.         out = self.relu(out)
  13.         out = self.linear2(out)
  14.         out = self.sigmoid(out)
  15.         return out
  17. model = NeuralNet(10,20)
  18. print(model)

从结果可以看出,我们建立的神经网络结构为: 连接层->ReLU层->连接层->Sigmoid函数层

如果中间有多个ReLU函数层,那么按照上面的思路,我们就需要定义relu1,relu2…等多个变量.

当然在定义激活层时, 我们可以将其放在forward()函数中,这样可以减少变量的定义

  1. class NeuralNet(nn.Module):
  2.     def __init__(self, input_size, hidden_size):
  3.         super(NeuralNet, self).__init__()
  4.         self.linear1 = nn.Linear(input_size, hidden_size)
  5.         self.linear2 = nn.Linear(hidden_size, 1)
  7.     # 将激活函数层直接放到 forward 中
  8.     def forward(self, x):
  9.         out = torch.relu(self.linear1(x))
  10.         out = torch.sigmoid(self.linear2(out))
  11.         return out
  14. # 测试代码
  15. model = NeuralNet(10, 20)
  16. model

这样写的话,在打印的时候就无法打印激活函数层了.因为激活函数层被放到了forward()中,只有调用forward()函数时,计算机才知道还需要激活处理

小结

本实验首先讲述了激活函数的主要形式以及用处,然后利用PyTorch建立了简单的神经网络模型