线性回归

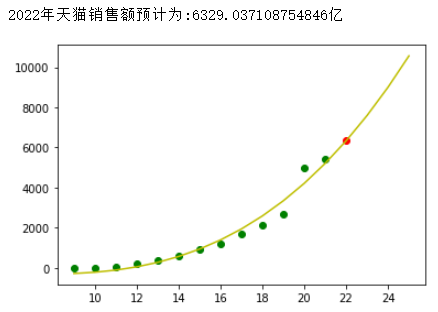
+本章我们的目的是想要通过编程的方式去预测房价以及天猫双十一2022年的销售额

线性回归

线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析, 简单来说线性回归其实是试图找到自变量与因变量之间的关系

例如已知房屋面积, 我们想要得到房屋价格, 即房屋面积与价格之间的关系

05_线性回归 - 图1

我们假设房价的趋势符合线性模型y = mx + b , 那么线性回归其实就是要求解最佳的m和b的值

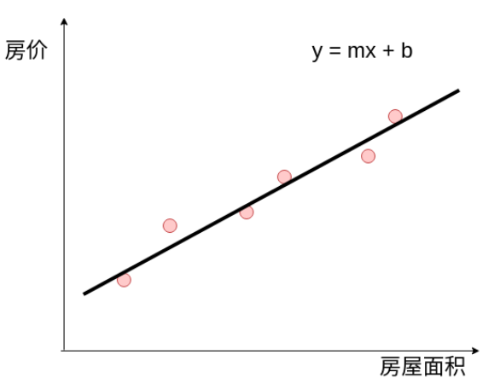
05_线性回归 - 图2

注意: 自变量可以有很多个, 例如房屋面积, 朝向, 卫生间的数量, 卧室数量, 到地铁站的距离都可以是自变量

为了便于方便大家后面的学习,我在这里先给大家准备一些测试用的假数据

面积	房价
80	200
95	230
104	245
112	247
125	259
135	262

代码数据准备

data = np.array([[80,200],
                 [95,230],
                 [104,245],
                 [112,247],
                 [125,259],
                 [135,262]])

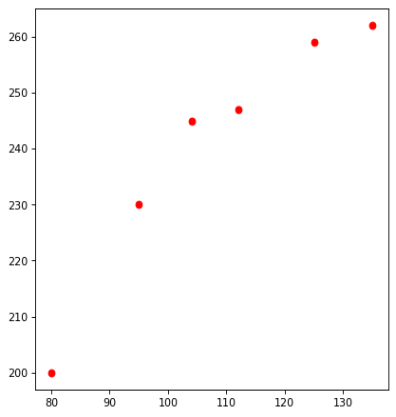
05_线性回归 - 图3

现在我想预测140平方的房屋的价格, 那么我们应该怎么做呢?

假设我们能根据上面的已有的数据, 求解出m和b的值, 那么我们也就可以预测140平方的房屋价格

MSE(Mean Squared Error)

均方误差是各数据偏离真实值的差值的平方和的平均数

05_线性回归 - 图4 %5E2%0A#card=math&code=MSE%20%3D%20%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28%E9%A2%84%E6%B5%8B%E5%80%BC%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC%29%5E2%0A)

例如, 假设张三和李四都来猜某套 05_线性回归 - 图5 房屋的价格, 每人有3次机会, 张三预测的价格为[a1,a2,a3] ,李四猜测的价格为[b1,b2,b3], 我们假设已知真实的房价为x, 现在我们需要一种算法来评估谁的预测更加准确, 这个时候我们就可以利用MSE, 谁的MSE越小, 说明猜测越接近真实值.

如果只看某个MSE是没有意义的, 没有对比就没有伤害, MSE要对比看才有意义,在猜测次数相同的情况下, MSE公式前面的$ \frac{1}{N}$ 保留和去掉关系不大,所以我们可以将上面的公式简化为:

05_线性回归 - 图6 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28%E9%A2%84%E6%B5%8B%E5%80%BC%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC%29%5E2%0A)

绘制数据与MSE之间的关系图

假设房价的走势复合循直线方程y = mx + b , 其中x表示的是房屋的面积, y表示的房屋的价格

任何一个复杂的问题, 我们应该想办法将它拆解成简单的问题, 所以我们先假设房屋的价格跟面积无关,只与b值相关, 所以我们令m = 0 的到的公式为:

05_线性回归 - 图7

可以简化为:

05_线性回归 - 图8

那么mse的计算公式为:

05_线性回归 - 图9 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28b%20-%20y%29%5E2%0A)

依据我们上面的分析,现在我们其实就是要找出一个合理的b, 可以让mse最小

为了便于大家更加直观的理解mse与b之间的关系, 我们利用代码将关系图绘制出来

# 导入绘图相关
# 将数据绘制出来
import matplotlib.pyplot as plt
# 假设b的取值1-300
b_range = np.linspace(1,400,50)
# 真实房屋价格
real_price = data[:,1]
# 绘制数据
for b in b_range:
    mse = np.sum((b - price)**2)
    plt.scatter(b,mse,c="red")
plt.show()

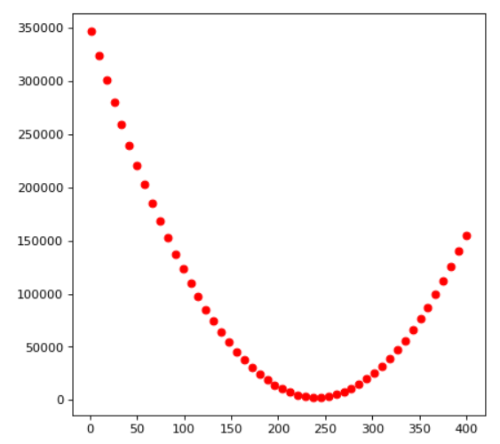
05_线性回归 - 图10

通过上图我们可以大概猜测, 当b = 240 左右的时候, mse最小. 那b具体应该等于多少呢?

还记得大明湖畔的导数吗?

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度, 速度的导数就是加速度.

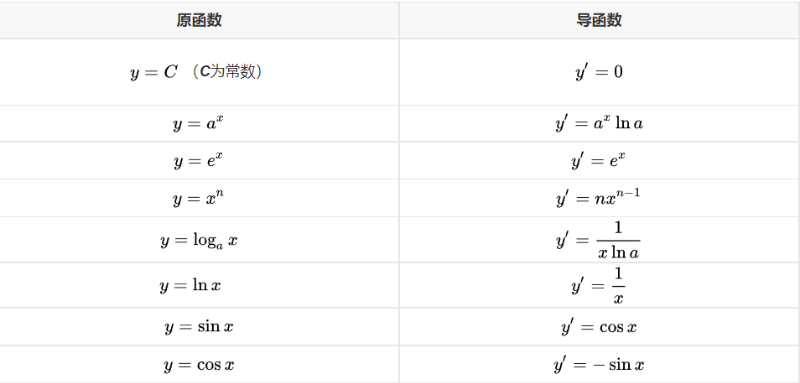
05_线性回归 - 图11

下面我们就用上面的公式来求解导函数,并将它的图绘制出来

原函数:

05_线性回归 - 图12 %20%3D%20x%5E2%20%2B%205%0A#card=math&code=f%28x%29%20%3D%20x%5E2%20%2B%205%0A)

导函数:

05_线性回归 - 图13 %20%3D%202%5Ccdot%20x%5E%7B(2-1)%7D%20%3D%202%5Ccdot%20x%0A#card=math&code=f%27%28x%29%20%3D%202%5Ccdot%20x%5E%7B%282-1%29%7D%20%3D%202%5Ccdot%20x%0A)

下面我们分别将原函数与导函数的图标绘制出来

原函数:

x = np.linspace(-100,100,100)
y = x**2 + 5
plt.figure()
plt.scatter(x,y,c="r")
plt.show()

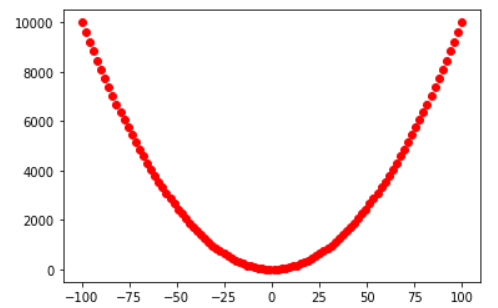
05_线性回归 - 图14

导函数:

x = np.linspace(-100,100,100)
y = 2*x
plt.figure()
plt.scatter(x,y,c="r")
plt.show()

05_线性回归 - 图15

根据导函数的公式, 我们可以随机挑几个数来算一下导数值

f'(-4) = -8
f'(-2) = -4
f'(2) = 4
f'(4) = 8

根据以上的计算我们可以得到这样的规律:

导数值为负, 增大x, mse下降

导数值为正, 减小x, mse下降

导数值负的越大, 小小的增加x, mse下降的多

导数值正的越大, 小小的减少x, mse下降的多

变化规律:

坡度越陡, 步伐应该小一点, 小心摔跤(小的学习速率)

坡度越平坦, 步伐应该大一点, 这样能更快到达底部(适当增加学习速率)

梯度下降

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

有时我们也将梯度的模称为梯度, 大白话讲就是梯度是朝着函数上升的方向去找最大值, 而我们的目标是要去找最小值, 所以我们要朝着函数下降的方向去找, 所以这就是我们要做的梯度下降

我们还是利用我们前面预测房价的案例来进行讲解, 首先我们回顾一下MSE的公式:

05_线性回归 - 图16 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28%E9%A2%84%E6%B5%8B%E5%80%BC%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC%29%5E2%0A)

依据我们定义的模型房价 = m*面积 + b, 我们可以写出下面这样的公式

05_线性回归 - 图17 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28m%5Ccdot%20%E9%9D%A2%E7%A7%AF_i%20%2B%20b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC_i%29%5E2%0A)

为了简单起见,我们先令m=0这样房价暂时与面积无关, 在上面我们就只有一个b值是需要求解的.

MSE现在是一个函数, b变化, MSE就会发生变化, 剩下的其它参数m,N,真实值这些都是已知的常数, 不会发生变化.

我们想要求解最小值, 只需要将MSE对b的导数计算出来就可以了:

05_线性回归 - 图18 %0A#card=math&code=%5Cfrac%7BMSE%7D%7B%5CDelta%20b%7D%20%3D%202%20%5Ctimes%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC_i%29%0A)

梯度下降的步骤

随机初始化b
计算这个b值对应的mse的斜率
如果mse的斜率非常大,那要根据根据mse的斜率,去修改b的值
mse值越大,b的修改值越大,mse斜率为正,b需要减少, mse斜率为负, b需要增加(朝着梯度的反方向去更新b)
选取一个很小的值,叫learningrate学习速率, 可以理解为下山迈开的步伐
用learningrate和mse的信号去更新b的值
重复2-6的步骤, 直到mse的斜率接近于0

代码实现

b = 1
learningrate = 0.01
def gradientdecent():
    global b
    mse = 0
    bslop = 0
    for real in data[:,1]:
        mse = mse + (b - real)**2
        bslop = bslop + (b - real) * 2
    # 拿到得到slop更新b 梯度的反方向
    b = b - bslop*learningrate
    print("b={},mse={}".format(b,mse))
    return b,mse

05_线性回归 - 图19

我们可以看到一定时间之后, b值与mse值不再变化, 即我们已经找到了最低点

思考题

为什么需要learningrate
为什么不需要直接求解%20%3D%200#card=math&code=%5Cfrac%7BMSE%7D%7B%5CDelta%20b%7D%20%3D%202%20%5Ctimes%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC_i%29%20%3D%200) 直接算出b的值?

求解y=mx+b

在上面的过程中, 我们为了简化我们令m=0,求出了b值, 很显然这是不符合实际情况的, 我们现在依然需要求解y = mx + b 中的m,x

自变量有多个的时候, 我们其实就是要单独求解每个自变量的偏导数的值了

我们先来看一下MSE的公式

05_线性回归 - 图21 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28%E9%A2%84%E6%B5%8B%E5%80%BC%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC%29%5E2%0A)

将y = mx + b 带到上面的公式中

05_线性回归 - 图22 %5E2%0A#card=math&code=MSE%20%3D%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28mx_i%20%2B%20b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC%29%5E2%0A)

然后我们在分别求MSE对b的偏导数和 MSE对m的偏导数

05_线性回归 - 图23 %0A#card=math&code=%5Cfrac%7BMSE%7D%7B%5CDelta%20b%7D%20%3D%202%20%5Ctimes%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28m%5Ccdot%20x_i%20%2B%20b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC_i%29%0A)

05_线性回归 - 图24 %5Ccdot%20x%0A#card=math&code=%5Cfrac%7BMSE%7D%7B%5CDelta%20m%7D%20%3D%202%20%5Ctimes%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28m%5Ccdot%20x_i%20%2B%20b%20-%20%E7%9C%9F%E5%AE%9E%E5%80%BC_i%29%5Ccdot%20x%0A)

感兴趣的同学,可以手工推导一下

代码实战

data = np.array([[80,200],
                 [95,230],
                 [104,245],
                 [112,247],
                 [125,259],
                 [135,262]])
# 初始化 m 和 b
m = 1
b = 1
learningrate = 0.00001
def gradientdecent():
    global m,b
    mse,mslop,bslop = 0,0,0
    # 计算mse
    for x_i,real_i in data:
        mse += (m * x_i + b - real_i)**2
        mslop += 2*(m*x_i + b - real_i)*x_i
        bslop += 2*(m*x_i + b - real_i)
    # 更新m,b的值
    m = m - mslop*learningrate
    b = b - bslop*learningrate
    # 打印数据
    print("m={},b={},mse={}".format(m,b,mse))
    return m,b,mse

经过若干次的梯度下降, 我们最终会发现m,b,mse的值几乎已经没有变化了,这意味着我们已经找到了最优解

m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353
m=1.0859355483580058,b=122.67599300309718,mse=257.2190856857353

拿着稳定的m,b的值,我们就可以预测140平米的房屋价格是多少房屋价格=m*140 + b

# 预测140平的房屋价格
import matplotlib.pyplot as plt
plt.figure()
for x,y in data:
    plt.scatter(x,y,c="black")
# 预测140
x1 = 140
y1 = m*140 + b
print("预测的140平米房价为:",y1)
plt.scatter(x1,y1,c="red")
# 绘制直线
XX = np.linspace(50,150,100)
plt.plot(XX,XX*m+b)
plt.show()

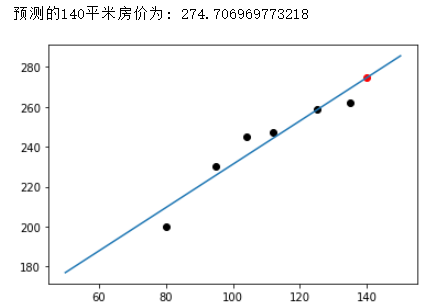
05_线性回归 - 图25

在上面的学习中,我们从1个参数的线性回归做到了2个参数的线性回归,如果有更多参数的线性回归, 我们其实就是要多算一些偏导数就可以啦!

线性回归的局限性

线性回归只适合线性问题. 如果数据模型是非线性的, 就得考虑使用的别的模型了.

例如下面的这种情况,数据比较离散

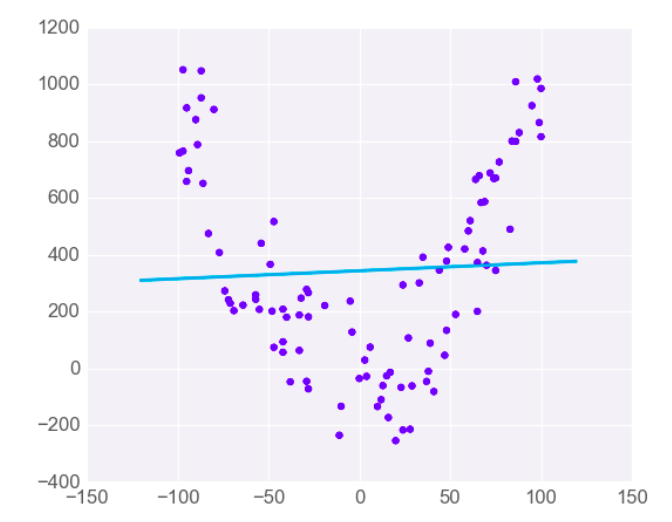
05_线性回归 - 图26

05_线性回归 - 图27

案例：预测天猫2022年双十一销售额

2009年交易额0.5亿；

2010年交易额9.36亿；

2011年交易额33.6亿；

2012年交易额191亿；

2013年交易额362亿元；

2014年交易额达571亿元；

2015年交易额912.17亿元；

2016年交易额1207亿元；

2017年交易额1682亿元；

2018年交易额2135亿元，首次突破2000亿大关；

2019年交易额2684亿元，14秒成交额破10亿，；

2020年交易额4982亿元；

2021年交易额5403亿元。

                #年份 销售额
data = np.array([[9,0.5], 
                 [10,9.36], 
                 [11,52], 
                 [12,191], 
                 [13,350.19], 
                 [14,571], 
                 [15,912.17], 
                 [16,1207], 
                 [17,1682], 
                 [18,2135],
                 [19,2684],
                 [20,4982],
                 [21,5403],
                ])

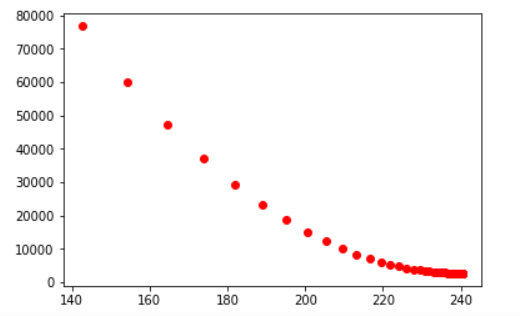
我们先将所有的数据在界面上绘制出来,看看它复合什么样的数学模型

plt.figure()
plt.scatter(data[:,0],data[:,1],c="r")
plt.show()

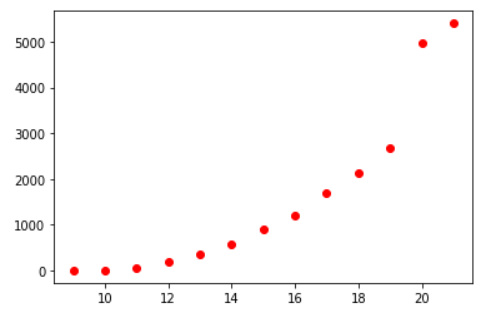
05_线性回归 - 图28

我们可以猜想,销售额的数据和三次方程比较接近, 我们可以尝试使用三次方程来进行求解

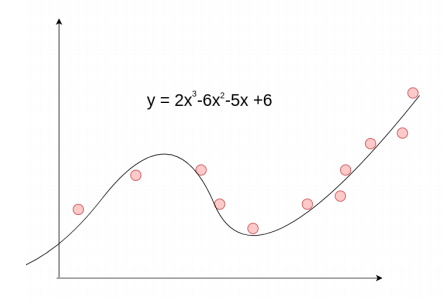
05_线性回归 - 图29

那么我们这里的公式就应该是:

05_线性回归 - 图30

这里我们需要求解的就是最优的m1,m2,m3,b, 也就是我们需要求4个偏导数

在此之前,我们都是手工推导的,在这里我们使用sympy 模块快速计算公式

from sympy import *
m1,m2,m3,b = symbols('m_1,m_2,m_3,b')
init_printing(pretty_print=True)
x_i,real_i,i = symbols("x_i,real_i,i")
expr = Sum((m1*x_i**3 + m2*x_i**2 + m3*x_i + b - real_i)**2,(i,2009,2021))

生成的mse公式如下:

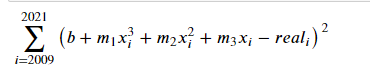
05_线性回归 - 图31

然后利用函数,求出mse对每一个变量的偏导数

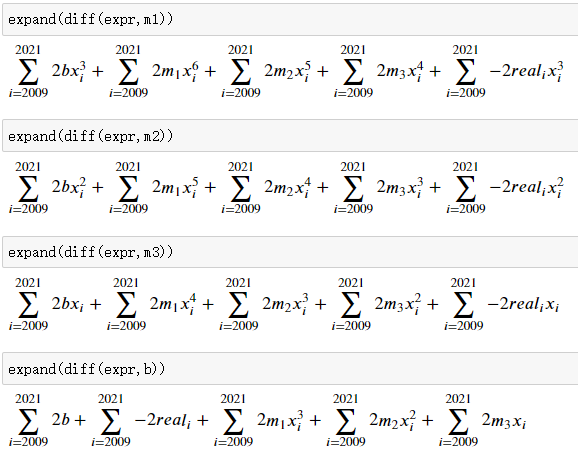
05_线性回归 - 图32

代码实现

m1,m2,m3,b = 1,1,1,1
learningrate = 0.000000001
np.set_printoptions(suppress=True)
def gradientdecent():
    global m1,m2,m3,b
    m1slop,m2slop,m3slop,bslop = 0,0,0,0
    mse = 0
    for x,real in data:
        mse += (b + m1*x**3 + m2*x**2 + m3*x - real)**2
        m1slop += 2*(b*x**3 + m1*x**6 + m2*x**5 + m3*x**4 - real*x**3)
        m2slop += 2*(b*x**2 + m1*x**5 + m2*x**4 + m3*x**3 - real*x**2)
        m3slop += 2*(b*x + m1*x**4 + m2*x**3 + m3*x**2 - real*x)
        bslop += 2*(b + m1*x**3 + m2*x**2 + m3*x - real)
    m1 = m1 - m1slop*learningrate
    m2 = m2 - m2slop*learningrate
    m3 = m3 - m3slop*learningrate
    b = b - bslop*learningrate
    print("m1={},m2={},m3={},b={},mse={}".format(m1,m2,m3,b,mse))
    return mse
# 训练数据
for i in range(100000):
    gradientdecent()

m1=1.2744148907956796,m2=-14.933041964792952,m3=-0.6688881515523788,b=0.8725331254366414,mse=1555807.967298704
m1=1.2744153755731444,m2=-14.933051063777576,m3=-0.6688853987223832,b=0.87253381115735,mse=1555807.8762188673
m1=1.2744158603297553,m2=-14.933060162380208,m3=-0.6688826458430032,b=0.8725344968830282,mse=1555807.785145726
m1=1.2744163450655126,m2=-14.933069260600867,m3=-0.6688798929142411,b=0.872535182613676,mse=1555807.6940792776
m1=1.2744168297804177,m2=-14.93307835843957,m3=-0.6688771399360992,b=0.8725358683492932,mse=1555807.6030195148
m1=1.2744173144744715,m2=-14.933087455896334,m3=-0.6688743869085796,b=0.8725365540898795,mse=1555807.5119664522
m1=1.2744177991476748,m2=-14.933096552971175,m3=-0.6688716338316845,b=0.8725372398354347,mse=1555807.4209200726
m1=1.2744182838000284,m2=-14.933105649664112,m3=-0.6688688807054161,b=0.8725379255859587,mse=1555807.329880387

使用如下代码进行绘图:

# 预测2022年天猫的销售额:
m1=1.27471243155291
m2=-14.93862843247405
m3=-0.6671664408115379
b=0.8729605947544549
def predict(x):
    y = m1*x**3 + m2*x**2 + m3*x + b
    print("2022年天猫销售额预计为:{}亿".format(y))
    return y
# predict(22)
plt.figure()
plt.scatter(data[:,0],data[:,1],c="g")
plt.scatter(22,predict(22),c="r")
x = np.linspace(9,25,25-9+1)
real =  m1*x**3 + m2*x**2 + m3*x + b
plt.plot(x,real,c="y")
plt.show()

05_线性回归 - 图33