基于卷积神经网络的CIFAR10网络

介绍

CIFAR10是由Hinton的两大弟子Alex Krizhevsky, IIya Sutskever收集的一个用于普通的物体识别的数据集. 本节我们将利用PyTorch建立一个卷积神经网络模型对CIFAR10中的数据集进行分类和识别.

知识点:

  1. CIFAR10
  2. 数据的预处理
  3. 卷积神经网络的相关概念
  4. 模型的搭建
  5. 模型的训练
  6. 模型的预测与应用

数据的预处理

CIFAR-10数据集由10个类的60000个32x32的彩色图像组成,即每个类有6000个图像. 数据如下所示:

15_卷积神经网络 - 图1

从上图可以看到,这10个类别分别是: 飞机,汽车,鸟,猫,鹿,狗,青蛙,马,船,卡车.每个类存在6000张图像,其中5000张在训练集,1000在测试集中. 即训练集中的图像总数为5000*10 = 50000张,测试数据集共有10000张图像. 让我们先定义出这些类别的名字.

classes = (“plane”,”car”,”bird”,”cat”,”deer”,”dog”,”frog”,”horse”,”ship”,”truck”)

我们的任务就是一个较好的模型, 使其能够对任意一张图像进行识别. 换句话说, 我们希望得到的模型为: 将任意一张图像放入该模型中, 该模型能够准确输出该图像的所属的类别.

首先, 这里我已经讲过数据集下载好了,我们直接调用即可!
在对数据进行读取之前, 我们可以添加一些预处理操作. 在前面章节中,我们已经学习torchvision.transforms.Compose()的使用方法. 我们可以通过该函数定义一个数据处理的集合,专门用于数据处理. 这里,我们对下载的图像进行的数据操作有: Tensor类型的转换 和 数据的标准化.

  1. import torch
  2. import torchvision
  3. import torchvision.transforms as transforms
  4. import numpy as np
  5. """
  6. transforms.Normalize
  7. 功能：对channel的对图像进行标准化（均值变为0，标准差变为1），可以加快模型的收敛
  8. output = (input - mean) / std
  9. mean:各通道的均值
  10. std：各通道的标准差
  11. """
  12. transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5))])
  15. # CIFAR10: 60000 张 32x32 大小的彩色图片，这些图片共分 10 类,每类有 6000 张图像
  16. # root:指定数据集所在位置
  17. # train=True：表示若本地已经存在，无需下载。若不存在，则下载
  18. # transform：预处理列表，这样就可以返回预处理后的数据集合
  19. train_dataset = torchvision.datasets.CIFAR10(root='./', train=True,
  20.                                              download=True, transform=transform)
  22. test_dataset = torchvision.datasets.CIFAR10(root='./', train=False,
  23.                                             download=True, transform=transform)
  24. print("训练集的图像数量为：", len(train_dataset))
  25. print("测试集的图像数量为", len(test_dataset))

上面得到的数据集就是标准化后的Tensor数据. torchvision.datasets.CIFAR10在运行时, 会查找root目录下是否存在所需要的数据集合. 如果存在, 则直接加载. 如果不存在, PyTorch会从官网上下载该数据集合.

得到数据之后,我们就可以利用torch.utils.data.DataLoader将数据集包装成一个数据生成器:

  1. batch_size = 4  # 设置批次个数
  2. # shuffle=True:表示加载数据前，会先打乱数据，提高模型的稳健性
  3. train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size,shuffle=True)
  5. test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size,shuffle=False)
  6. test_loader, test_loader

接下来,我们就可以利用已经定义好的数据加载器,加载几张图片,观察一下图片的具体效果

  1. import matplotlib.pyplot as plt
  3. def imshow(img):
  4.     # 由于加载器产生的图片是归一化后的图片,因此这里需要将图片反归一化
  5.     img = img*0.5 + 0.5
  6.     # 将图像从Tensor转为numpy
  7.     npimg = img.numpy()
  8.     # 产生的数据为 C×W×H 而 plt 展示的图像一般都是 W×H×C
  9.     # 因此，这里会有一个维度的变换
  10.     plt.imshow(np.transpose(npimg, (1, 2, 0)))
  11.     plt.show()
  14. # 随机获得一些训练图像
  15. dataiter = iter(train_loader)
  16. images,labels = dataiter.next()
  18. # 将这些图像进行展示
  19. imshow(torchvision.utils.make_grid(images))

你可以多次运行上面代码, 观察数据集中的图像. 由于这些图像只有32x32的大小, 因此我们会感觉这些图像分辨率不是很高.

其实这种大小的图像是非常好的,因为这种小图像在保存原有内容的条件下,能够尽可能的加快模型的训练速度(图像越大,建立的神经网络就会越大,模型训练的时间就会越长)

模型的建立

此次我们将使用卷积神经网络对CIFAR10进行识别. 除了线性连接层, 激活函数层外, 卷积神经网络比全连接网络还多了卷积层和池化层.

卷积运算其实属于分析数学中的一种运算方式. 卷积层的主要目的就是对图像进行卷积进而达到提取图像特征的效果. 针对图像的特征提取,一般使用的卷积/

卷积过程起始就是将滤波器当作是滑动窗口,然后对整个图像进行滑动计算:

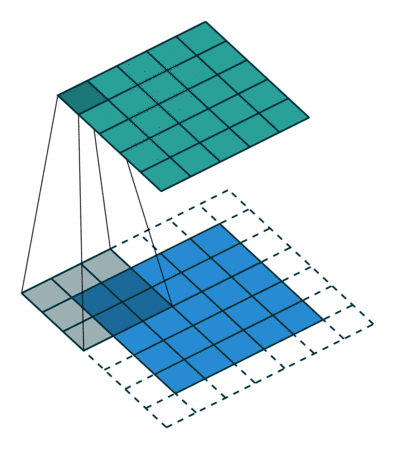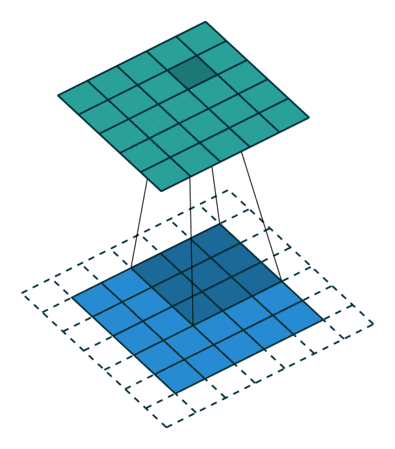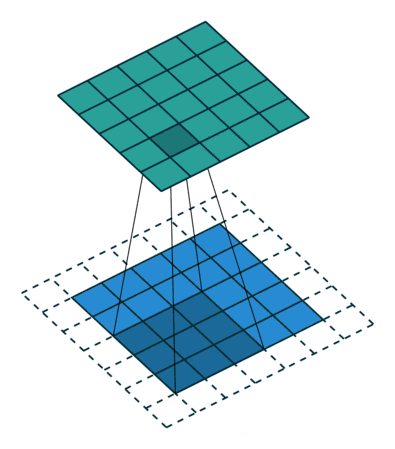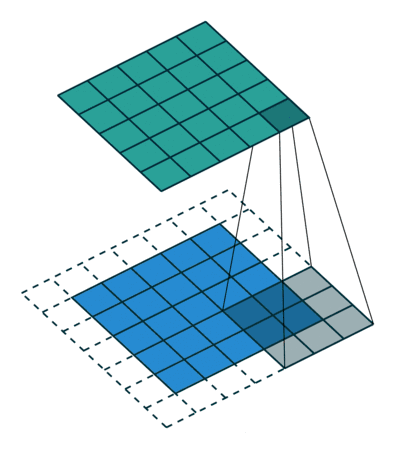
15_卷积神经网络 - 图2

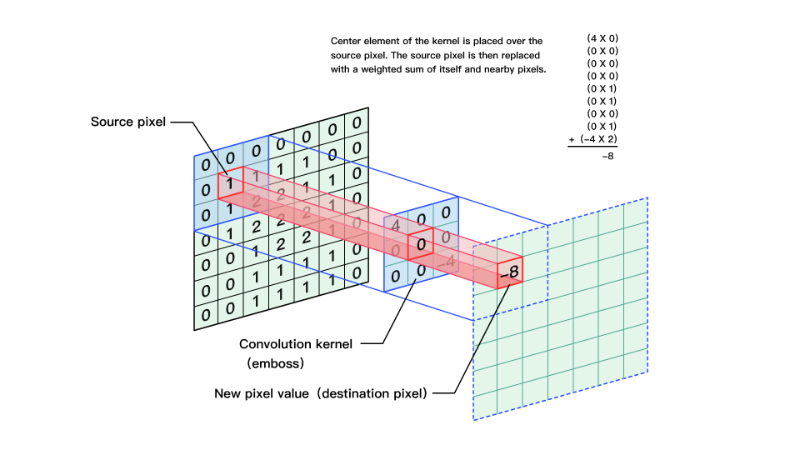
15_卷积神经网络 - 图3

在pytorch中,我们使用nn.Conv2d(input_channel, out_channel,filter_size)进行卷积操作.

  • input_channel : 表示输入图层的通道数
  • out_channel: 表示输出图层的通道数
  • filter_size: 表示过滤器的大小

池化层主要用于对数据和参数量的压缩. 池化操作的过程其实就是把输入图像划分成多个矩形区域, 每个区域进行一次池化,得到一个值. 最后, 将每个区域输出的值进行排列得到最终的池化结果

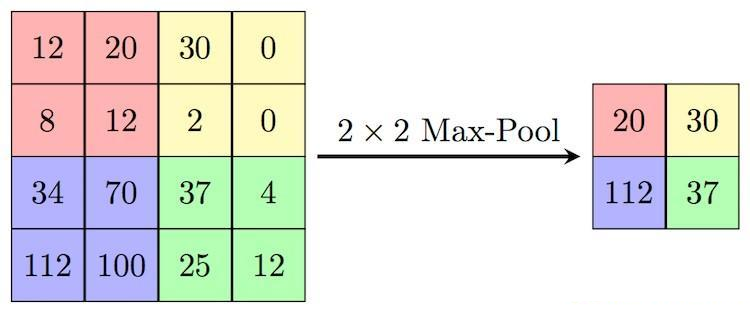
15_卷积神经网络 - 图4

池化操作有很多种,其中最常见的池化操作就是最大池化和平均池化.而上图阐述的就是最大池化操作. 将输入图层放入了一个最大池化层中,然后输入图层被分割成了4个区域,取每个区域内的最大值作为该区域的输出值,再把这些值排列起来,形成池化结果. 同理, 平均池化就是输出每个区域中的平均值. 池化操作可以去除图像中冗余信息, 有效防止模型的过拟合.

在PyTorch中,我们可以使用torch.nn.MaxPool2d(kernel_size,stride)来进行最大池化操作

  • kernel_size : 滤波器的大小
  • stride: 步长

为了能够识别CIFAR数据集, 我们将利用PyTorch建立一个能够对CIFAR数据集进行分类的网络模型. 该网络模型结构如下:

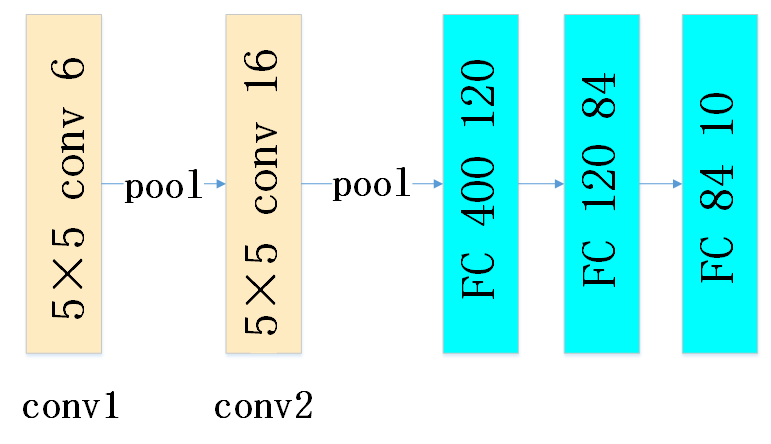
15_卷积神经网络 - 图5

其中conv1和conv2是卷积核大小为5x5的卷积层. 这两个卷积层的输入和输出是不同. fc1,fc2,fc3为3个全连接层.conv1和conv2之间存在一个池化层. conv2和fc1之间存在一个池化层.这些卷积层,池化层和全连接层之间都有一个激活函数层. 一般我们常说的神经网络层其实就是网络层加激活函数层. 因此, 这里我们并没有将激活函数层画出来,不过在代码实现时, 应当有激活函数层.

让我们利用PyTorch代码来对其进行实现

  1. import torch.nn.functional as F
  2. import torch.nn as nn
  4. # 网络模型的建立
  7. class ConvNet(nn.Module):
  8.     def __init__(self):
  9.         super(ConvNet, self).__init__()
  10.         # 神经网络的输入为 三个通道
  11.         self.conv1 = nn.Conv2d(3, 6, 5)
  12.         self.pool = nn.MaxPool2d(2, 2)
  13.         self.conv2 = nn.Conv2d(6, 16, 5)
  14.         self.fc1 = nn.Linear(16 * 5 * 5, 120)
  15.         self.fc2 = nn.Linear(120, 84)
  16.         # 由于一共有 10 个类，因此模型的输出节点数量为 10
  17.         self.fc3 = nn.Linear(84, 10)
  19.     def forward(self, x):
  20.         # -> n, 3, 32, 32
  21.         # 传入数据，且为输出数据添加激活函数
  22.         x = self.pool(F.relu(self.conv1(x)))  # -> n, 6, 14, 14
  23.         x = self.pool(F.relu(self.conv2(x)))  # -> n, 16, 5, 5
  24.         x = x.view(-1, 16 * 5 * 5)            # -> n, 400
  25.         x = F.relu(self.fc1(x))               # -> n, 120
  26.         x = F.relu(self.fc2(x))               # -> n, 84
  27.         x = self.fc3(x)                       # -> n, 10
  28.         return x
  31. # 定义当前设备是否支持 GPU
  32. device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
  33. model = ConvNet().to(device)
  34. model

建立完模型后, 接下来, 让我们对损失函数和优化器进行定义.这里我们使用交叉熵作为模型的损失函数,使用SGD算法作为梯度下降的优化器:

  1. learning_rate = 0.001
  2. criterion = nn.CrossEntropyLoss()
  3. optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
  4. criterion, optimizer

上面的代码结果可以看出, 我们所编写的模型结构和上面的图形一致

模型的训练

模型的训练步骤是固定的,我们只需要在编写时,注意模型的输入即可. 如果是全连接神经网络,我们需要将图片转为一个行向量,即每行代表一条数据.如果是卷积神经网络,我们就可以直接将图片作为输入. 当然, 在输入时,我们也需要注意模型的输入大小和图片的大小是否一致.

模型训练的步骤和上一章节一致

  • 通过模型的正向传播,输出预测结果
  • 通过预测结果和真实标签计算损失
  • 通过反向传播,获得梯度
  • 通过梯度更新模型的权重
  • 进行梯度的清空
  • 循环上面的操作,直到损失较小为止

由于这里使用的是CPU运行, 因此训练速度较慢.

  1. num_epochs = 5
  2. # 定义数据长度
  3. n_total_steps = len(train_loader)
  4. print("Start training....")
  5. for epoch in range(num_epochs):
  6.     for i, (images, labels) in enumerate(train_loader):
  7.         # 原始数据集的大小，每个批次的大小为: [4, 3, 32, 32]
  8.         # 将数据转为模型支持的环境类型。
  9.         images = images.to(device)
  10.         labels = labels.to(device)
  12.         # 模型的正向传播，得到数据数据的预测值
  13.         outputs = model(images)
  14.         # 根据预测值计算损失
  15.         loss = criterion(outputs, labels)
  17.         # 固定步骤：梯度清空、反向传播、参数更新
  18.         optimizer.zero_grad()
  19.         loss.backward()
  20.         optimizer.step()
  22.         if (i+1) % 2000 == 0:
  23.             print(
  24.                 f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{n_total_steps}], Loss: {loss.item():.4f}')
  27. print('Finished Training')

为了保证训练模型在后面的使用,在完成模型的训练后, 我们一般都会将模型持久化,即保存起来,方便以后使用

我们通过torch.save(model, PATH)来讲指定模型model保存到PATH中

  1. PATH="./conv.pt"
  2. torch.save(model.state_dict(), PATH)
  3. print("模型已经保存完成")

模型的测试

接下来,让我们加载本地已经保存好的模型, 进行模型的预测

由于我们这里的模型训练和测试是一气呵成的,因此内存中存在已训练的模型. 但是为了讲解模型加载的知识点, 这里我们还是从本地读取刚才训练好的模型.

我们通过model.load_state_dict(torch.load(PATH))来加载本地的模型:

  1. new_model = ConvNet()
  2. new_model.load_state_dict(torch.load(PATH))

接下来, 我们将利用测试集来计算模型的总识别准确率一级每一类图像的识别准确率

  1. with torch.no_grad():
  2.     # 统计预测正确的图像数量和进行了预测的图像数量
  3.     n_correct = 0
  4.     n_samples = 0
  5.     # 统计每类图像中，预测正确的图像数量和该类图像的实际数量
  6.     n_class_correct = [0 for i in range(10)]
  7.     n_class_samples = [0 for i in range(10)]
  8.     for images, labels in test_loader:
  9.         images = images.to(device)
  10.         labels = labels.to(device)
  11.         outputs = new_model(images)
  12.         # 利用 max 函数返回 10 个类别中概率最大的下标，即预测的类别
  13.         _, predicted = torch.max(outputs, 1)
  14.         n_samples += labels.size(0)
  15.         # 通过判断预测值和真实标签是否相同，来统计预测正确的样本数
  16.         n_correct += (predicted == labels).sum().item()
  17.         # 计算每种种类的预测正确数
  18.         for i in range(batch_size):
  19.             label = labels[i]
  20.             pred = predicted[i]
  21.             if (label == pred):
  22.                 n_class_correct[label] += 1
  23.             n_class_samples[label] += 1
  24.     # 输出总的模型准确率
  25.     acc = 100.0 * n_correct / n_samples
  26.     print(f'Accuracy of the network: {acc} %')
  28.     # 输出每个类别的模型准确率
  29.     for i in range(10):
  30.         acc = 100.0 * n_class_correct[i] / n_class_samples[i]
  31.         print(f'Accuracy of {classes[i]}: {acc} %')

从结果可以看出, 我们建立的模型的识别准确率不是很高. 这其实是多方面的原因, 首先是我们建立的卷积神经网络模型还不够深, 没有提取到更多有用的图像特征. 其次, 是我们迭代的次数还不够多, 损失还没有降到最低. 上面我们案例我们仅仅为了了解PyTorch的具体用法.

如果需要一个具有更高识别率的模型,我们就需要建立一个更深的神经网络, VGG16,用于数据集合的识别

VGG16模型

通过下面的代码,我们知道VGG16看起来非常复杂.但仔细观察,该模型和上面模型的组件相同. 即都是由卷积层,全连接层,激活函数,池化层等组成的. 下面代码, 无需手敲,直接运行即可. 当然, 如果你想更加深入学习,也可以自己推敲下面网络结构

  1. import torch.nn.functional as F
  2. import torch.nn as nn
  4. # 网络模型的建立
  7. class VGG16(nn.Module):
  8.     def __init__(self, num_classes=10):
  9.         super(VGG16, self).__init__()
  10.         self.features = nn.Sequential(
  11.             # 1
  12.             nn.Conv2d(3, 64, kernel_size=3, padding=1),
  13.             nn.BatchNorm2d(64), #数据归一化 均值为0 方差为1
  14.             nn.ReLU(True),
  15.             # 2
  16.             nn.Conv2d(64, 64, kernel_size=3, padding=1),
  17.             nn.BatchNorm2d(64),
  18.             nn.ReLU(True),
  19.             nn.MaxPool2d(kernel_size=2, stride=2),
  20.             # 3
  21.             nn.Conv2d(64, 128, kernel_size=3, padding=1),
  22.             nn.BatchNorm2d(128),
  23.             nn.ReLU(True),
  24.             # 4
  25.             nn.Conv2d(128, 128, kernel_size=3, padding=1),
  26.             nn.BatchNorm2d(128),
  27.             nn.ReLU(True),
  28.             nn.MaxPool2d(kernel_size=2, stride=2),
  29.             # 5
  30.             nn.Conv2d(128, 256, kernel_size=3, padding=1),
  31.             nn.BatchNorm2d(256),
  32.             nn.ReLU(True),
  33.             # 6
  34.             nn.Conv2d(256, 256, kernel_size=3, padding=1),
  35.             nn.BatchNorm2d(256),
  36.             nn.ReLU(True),
  37.             # 7
  38.             nn.Conv2d(256, 256, kernel_size=3, padding=1),
  39.             nn.BatchNorm2d(256),
  40.             nn.ReLU(True),
  41.             nn.MaxPool2d(kernel_size=2, stride=2),
  42.             # 8
  43.             nn.Conv2d(256, 512, kernel_size=3, padding=1),
  44.             nn.BatchNorm2d(512),
  45.             nn.ReLU(True),
  46.             # 9
  47.             nn.Conv2d(512, 512, kernel_size=3, padding=1),
  48.             nn.BatchNorm2d(512),
  49.             nn.ReLU(True),
  50.             # 10
  51.             nn.Conv2d(512, 512, kernel_size=3, padding=1),
  52.             nn.BatchNorm2d(512),
  53.             nn.ReLU(True),
  54.             nn.MaxPool2d(kernel_size=2, stride=2),
  55.             # 11
  56.             nn.Conv2d(512, 512, kernel_size=3, padding=1),
  57.             nn.BatchNorm2d(512),
  58.             nn.ReLU(True),
  59.             # 12
  60.             nn.Conv2d(512, 512, kernel_size=3, padding=1),
  61.             nn.BatchNorm2d(512),
  62.             nn.ReLU(True),
  63.             # 13
  64.             nn.Conv2d(512, 512, kernel_size=3, padding=1),
  65.             nn.BatchNorm2d(512),
  66.             nn.ReLU(True),
  67.             nn.MaxPool2d(kernel_size=2, stride=2),
  68.             nn.AvgPool2d(kernel_size=1, stride=1),
  69.         )
  70.         self.classifier = nn.Sequential(
  71.             # 14
  72.             nn.Linear(512, 4096),
  73.             nn.ReLU(True),
  74.             nn.Dropout(),
  75.             # 15
  76.             nn.Linear(4096, 4096),
  77.             nn.ReLU(True),
  78.             nn.Dropout(),
  79.             # 16
  80.             nn.Linear(4096, num_classes),
  81.         )
  82.         #self.classifier = nn.Linear(512, 10)
  84.     def forward(self, x):
  85.         out = self.features(x)
  86.         out = out.view(out.size(0), -1)
  87.         out = self.classifier(out)
  88.         return out
  91. # 定义当前设备是否支持 GPU
  92. device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
  93. model = VGG16().to(device)
  94. model

同理,我们在模型训练时, 也需要增加迭代次数, 将迭代次数增加到20. 由于训练一个深度神经网络是非常缓慢的. 因此, 这里我不再对上面神经网络进行训练.

下面, 我们直接利用model.load_state_dict(torch.load(PATH))加载我已经训练好的模型.

注意: 在CPU环境下加载GPU运行的模型时, 我们需要添加map_location="cpu"

  1. new_model = VGG16().to(device)
  2. new_model.load_state_dict(torch.load("vggcnn.pt", map_location="cpu"))
  3. print("加载模型")

和上面模型测试一样, 让我们将测试数据放入模型中, 计算VGG模型的识别准确率

  1. # 重新下设置 batch_size，使模型一次能够预测更多的数据
  2. test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=125,
  3.                                           shuffle=False)
  4. with torch.no_grad():
  5.     # 统计预测正确的图像数量和进行了预测的图像数量
  6.     n_correct = 0
  7.     n_samples = 0
  8.     i = 0
  9.     for images, labels in test_loader:
  10.         images = images.to(device)
  11.         labels = labels.to(device)
  12.         outputs = new_model(images)
  13.         # 利用 max 函数返回 10 个类别中概率最大的下标，即预测的类别
  14.         _, predicted = torch.max(outputs, 1)
  15.         n_samples += labels.size(0)
  16.         # 通过判断预测值和真实标签是否相同，来统计预测正确的样本数
  17.         n_correct += (predicted == labels).sum().item()
  18.         if i % 10 == 0:
  19.             print("已预测完第{}批次的数据".format(i))
  20.         i = i+1
  22.     # 输出总的模型准确率
  23.     acc = 100.0 * n_correct / n_samples
  24.     print(f'VGG模型的识别准确率为: {acc} %')

从结果可以看到,仅仅迭代20次,VGG16模型的识别准确率就可以达到78%左右.

结论: 网络模型结构越深,得到的细节越多, 对物体的识别能力越强. 当然, 任何事物都有两面性, 随着网络模型的加深, 我们的训练难度和训练成本也会提高. 因此, 如何在模型识别准确率和训练之间寻找一个平衡是研究界的一个重要方向.

小结

本节我们介绍了CIFAR10数据集,利用相关函数对它进行了预处理. 然后, 根据卷积神经网络的相关知识, 利用PyTorch建立相关神经网络模型. 接着, 定义了损失和优化器, 对模型进行了训练. 最后将提前分割出来的测试集放入模型进行预测, 得到已训练模型的识别准确率.