梯度下降算法

概述

本节我们主要讲解梯度下降算法, 使用手写梯度下降算法解决线性回归问题. 最后对PyTorch中的反向传播函数进行了讲解并利用该函数简明快速的完成了损失的求导与模型的训练.

1. 线性回归
2. 梯度下降算法
3. 损失函数

   梯度下降算法

线性回归

线性回归问题其实就是找一条合适的直线y = wx 用以表示所有的数据点: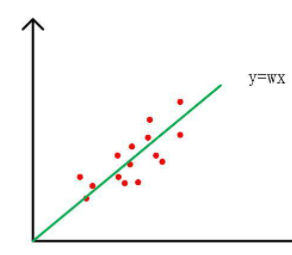

如上图所示, 线性回归问题其实就是求解上面的线性函数中最佳的w值. 合适y = wx 函数可以表示标签Y和数据X之间的关系,进而预测新的x所对应的预测值y_pre, 其中y_pre = wx. 那么我们应当用什么来衡量最佳的w值呢?

我们一般认为y_pre和真实值y的距离越小, 那么该函数就越好, w的值就趋近于最佳. 在机器学习中, 这种计算距离的函数有一个名字, 叫做损失函数.

import numpy as np
def loss(y, y_pred):
    return ((y_pred - y)**2).mean()
# 测试代码
y_pred = np.array([1,2])
y = np.array([1.1])
loss(y, y_pred)

综上, 线性回归的问题其实就是求解损失函数最小的情况下的w值

梯度下降算法

梯度下降算法是一种用于求解函数极小值的方法.

我们可以把梯度下降算法类比为一个下山的过程. 假设一个人被困在山上, 需要快速从山上下来, 走到山底. 但是, 由于山中浓雾很大, 导致可视度很低. 因此, 我们无法确定下山的路径,只能看周围的一些信息. 也就是说我们需要走一步看一步再走一步。此时，我们就需要梯度下降的算法

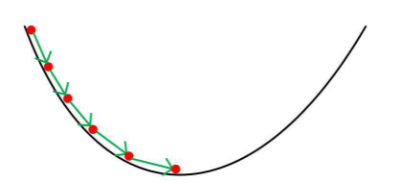
我们可以把损失函数看作是一座山，我们的目标就是找到这座山的最小值，即山底。 每走一步， 我们都会重新找山脚的方向。因为沿着山脚的方向走能够使我们最快到达山脚的位置。 由于梯度表示的是函数上升最快的方向， 因此梯度反方向应该是函数下降最快的方向。 我们每次到了一个新的位置， 就会计算该位置的梯度， 找到下一步下山最快的方向。 根据梯度和当前位置更新下一次所在位置的数学表达式:

%0A#card=math&code=%5Ctheta%5E1%20%3D%20%5Ctheta%5E0%20-%20%5Calpha%20%5Ccdot%20%E2%96%BDJ%28%5Ctheta%5E0%29%0A&id=hFO1k)

上面式子展示了损失函数J(θ)的最小值求解过程

其中表示当前所在位置,表示下一步的位置, 表示步长(即一次更新的距离 , #card=math&code=-%E2%96%BDJ%28%5Ctheta%5E0%29&id=FJGnH) 表示损失函数的梯度相反方向

我们讲损失函数值J定义为欧式距离:

%5E2%0A#card=math&code=J%20%3D%20%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28w%5Ccdot%20x_i%20-%20y_i%29%5E2%0A&id=FGNKP)

损失函数关于w的梯度为:

%0A#card=math&code=%5Cfrac%7B%5Cpartial%20J%7D%7B%5Cpartial%20w%7D%20%3D%20%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7D%282w%5Ccdot%20x_i%5E2%20-%202x_i%20y_i%29%0A&id=tUysb)

根据上面的梯度公式,我们可以来定义损失函数的梯度计算公式

# dj/dw
def gradient(x, y, w):
    return np.mean(2*w*x*x - 2*x*y)
# 测试代码
x = np.array([1, 2])
y = np.array([1, 1])
gradient(x, y, 2)

梯度下降算法实现步骤

假设w为损失函数需要的变量, 那么梯度下降算法的具体步骤如下:

1. 随机初始化一个w的值
2. 在该w下进行正向传播,得到所有x的预测值y_pre
3. 通过实际的值y和预测值y_pre计算损失
4. 通过损失计算梯度dw
5. 更新w: w = w - lr*dw . 其中lr为补偿,可自定义的值
6. 重复步骤2 - 5, 直到损失降到较小位置

首先, 让我们先来定义一下梯度下降算法所需要的数据集和变量值

# 正向传播,计算预测值
def forward(x):
    return w*x
# 定义数据集 , w 初始化
X = np.array([1,2,3,4], dtype=np.float32)
Y = np.array([2,4,6,8], dtype=np.float32)
w = 0.0
# 定义步长和迭代次数
learning_rate = 0.01
n_iters = 20

接下来, 让我们根据上面步骤, 利用梯度下降算法求解一元回归函数中的w值:

for epoch in range(n_iters):
    y_pred = forward(X)
    # 计算损失
    l = loss(Y, y_pred)
    # 计算梯度
    dw = graident(X,Y,w)
    # 更新参数
    w = w - learning_rate * dw
    if epoch%2 == 0:
        print(f"epoch {epoch+1}:w={w:.3f},loss={l:.8f}")

从结果可以很清晰看出利用梯度下降算法,不断降低损失的值,寻找最佳的权重参数w. 当损失不再发生变化时, 证明我们已经找到了一个较小的值, 此时的w就是较佳权重. 即线性函数y=2x可以很好的表示上面的数据集合.

利用PyTorch实现梯度下降算法

线性函数的损失函数的梯度公式很容易被推导出来,因此我们能手动的完成梯度下降算法. 但是, 在很多机器学习中, 模型的函数表达式非常复杂的, 这个时候手动定义该函数的梯度函数需要非常强的数学功底. 因此, 这里我们使用上一个实验中所用的后向传播函数来实现梯度下降算法.求解最佳权重w.

首先, 让我们来定义数据集合以及w的初始值,并将其设置为可以求偏导的张量

import torch
X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
Y = torch.tensor([2, 4, 6, 8], dtype=torch.float32)
# 初始化权重参数w
w = torch.tensor(0, dtype=torch.float32, requires_grad=True)
# 定义步长和迭代次数
learning_rate = 0.01
n_iters = 20

接下来让我们使用.backward()直接求解梯度

for epoch in range(n_iters):
    y_pred = forward(X)
    l = loss(Y, y_pred)
    # 无需定义梯度求解函数,直接求解梯度
    l.backward()
    # 利用梯度下降更新参数
    with torch.no_grad():
        w.data = w.data - learning_rate*w.grad
    # 清空梯度
    w.grad.zero_()
    if epoch%2 == 0:
        print(f"epoch {epoch}: w={w.item():.3f}, loss={l.item():.8f})
print(f"根据训练模型预测,当x=5时,y的值为:{forward(5):.3f}")

可以看到, 利用PyTorch进行梯度下降的结果和人工梯度下降结果一致.我们通过.backward(), 简洁明了的求取任何复杂函数的梯度,大大的节约了我们公式推导的时间

小结

本节我们主要讲解梯度下降算法以及利用.backward()对损失进行求导