乳腺癌的预测

介绍

本节我们以乳腺癌的预测为实例,阐述PyTorch求解一个非线性的问题

  1. 数据集的标准化
  2. 数据集的划分
  3. Sigmoid函数
  4. 乳腺癌的预测

    数据集的预处理

首先,让我们来加载数据集合.这里我们使用pandas对数据集合进行加载

  1. # 预测乳腺癌,使用pandas对数据集合进行加载
  2. import pandas as pd 
  4. df = pd.read_csv("./breast_cancer.csv")

从结果中我们知道该数据集合中共有569条数据,每条数据有30个和乳腺癌相关的病变特征,最后一列是该患者是否患有乳腺癌的诊断结果. 其中0表示没有患有乳腺癌,1表示患有乳腺癌.

我们可以利用pandas中的切片,先将上表中的特征和标签分开

  1. # 每行数据有30个乳腺病理特征, 最后一列表示是否患有乳腺癌
  2. X = df[df.columns[0:-1]].values
  3. Y = df[df.columns[-1]].values
  4. print(X.shape,Y.shape)

可以看到共有569条数据,每条数据有30个特征和1个标签

数据集的划分和标准化

为了能够评估模型的好坏, 我们利用sklearn.model_selection函数,将原数据按比例随机分为训练集数据和测试集数据

  1. from sklearn.model_selection import train_test_split
  2. # 按照0.8 和 0.2 的比例随机划分数据集合
  3. X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2,random_state=1234)
  4. print(X_train.shape,Y_train.shape,X_test.shape,Y_test.shape)

为了加快模型的收敛速度,一般我们都需要对原始数据进行标准化处理,将所有的数据按照比例缩放到一定范围内.这里我们可以使用sklearn.preprocessing来对数据集合进行标准化

  1. from sklearn.preprocessing import StandardScaler
  2. sc = StandardScaler()
  3. # 对特征进行标准化
  4. X_train = sc.fit_transform(X_train)
  5. X_test = sc.fit_transform(X_test)

最后, 为了将数据放入PyTorch定义的模型之中, 我们必须将所有的数据转为张量类型:

  1. import torch
  2. import numpy as np
  3. X_train = torch.from_numpy(X_train.astype(np.float32))
  4. Y_train = torch.from_numpy(Y_train.astype(np.float32))
  6. X_test = torch.from_numpy(X_test.astype(np.float32))
  7. Y_test = torch.from_numpy(Y_test.astype(np.float32))
  9. # 将标签转成2维
  10. Y_train = Y_train.view(Y_train.shape[0],1)
  11. Y_test = Y_test.view(Y_test.shape[0],1)
  12. print(X_train.size(),Y_train.size())

乳腺癌的预测

模型的定义

在处理完数据后,接下来, 我们就需要建立相应的模型,用于乳腺癌的预测了.

线性函数是一条没有上界和下界的直线, 即线性函数预测出来的值可以很大, 也可以非常小. 而实验数据的标签只有0(患病)或1(不患病), 因此用线性函数来拟合乳腺癌的数据点是不合理的.

我们需要找到输出始终为0-1之间的函数模型.如果拥有这样的函数模型,那么将任意的x放入该模型中,都会输出0-1之间的值.这个值我们可以看做说患有乳腺癌的概率.如果这个概率值小于0.5则表示没有患乳腺癌.如果这个概率值大于0.5则表示患有乳腺癌.

逻辑回归函数Sigmoid就是这样的一种函数,该函数又叫做激活函数:

12_案例：乳腺癌的预测 - 图1

该函数的几何图形如下所示: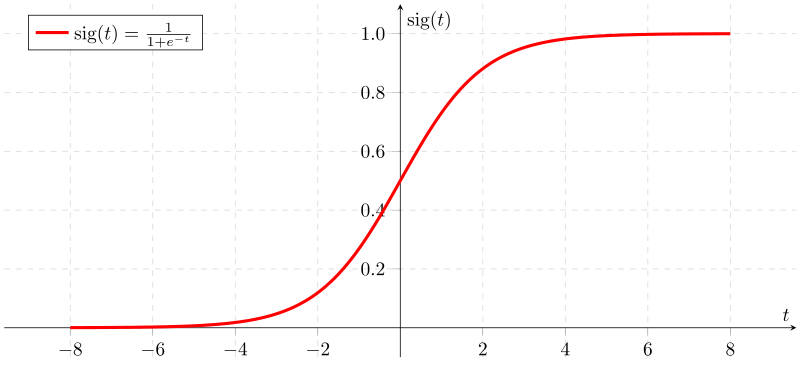
12_案例：乳腺癌的预测 - 图2
12_案例：乳腺癌的预测 - 图3

从图中我们可以看出,该函数就是一个上下界分别为1和0的有界非线性函数.

我们可以将线性函数的输出,经过上面的激活函数处理,得到0-1之间的结果

综上, 预测乳腺癌的模型如下:

  1. import torch.nn as nn
  3. class Model(nn.Module):
  4.     def __init__(self,n_input_features):
  5.         super(Model,self).__init__()
  6.         self.linear = nn.Linear(n_input_features,1)
  8.     def forward(self,x):
  9.         y_pred = torch.sigmoid(self.linear(x))
  10.         return y_pred
  12. # 获取样本量和特征数
  13. n_samples,n_features = X.shape
  14. # 模型的初始化
  15. model = Model(n_features)
  16. # 损失函数公式
  17. loss = nn.BCELoss()
  18. # 迭代次数
  19. num_epochs = 100
  20. # 学习率
  21. learning_rate = 0.1
  22. # 优化器
  23. optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)

模型的训练

定义完损失函数和优化器后,接下来的模型训练步骤就是固定的了,如下:

  • 通过模型的正向传播,输出预测结果
  • 通过预测结果和真实标签计算损失
  • 通过反向传播,获取梯度
  • 通过梯度更新模型的权重
  • 进行梯度的清空
  • 循环上面的操作,直到损失较小为止

让我们用代码完成上面的步骤:

  1. # 固定步骤: 1.正向传播,模型预测 2.计算损失 3.对损失计算梯度 4.更新权重 5.清空梯度 6.循环上述步骤
  2. for epoch in range(num_epochs):
  3.     y_pred = model(X_train)
  4.     l = loss(y_pred,Y_train)
  5.     # 反向传播
  6.     l.backward()
  7.     # 更新权重
  8.     optimizer.step()
  9.     # 清空梯度
  10.     optimizer.zero_grad()
  12.     if epoch%5 == 0:
  13.         print(f"epoch:{epoch},loss={l.item():.4f}")
  15. print("模型训练完成")

综上,我们训练好了一个乳腺癌的预测模型. 我们可以尝试对任意一条数据进行预测

  1. index = np.random.randint(0,len(X_test))
  2. y_pred = model(X_test[index])
  4. y_pred_label = y_pred.round()
  5. # 将结果转为numpy类型
  6. real = Y_test[index].detach().numpy()[0]
  7. pre = y_pred_label.detach().numpy()[0]
  9. print(f"第{index}条数据的真实结果为:{real},预测结果为:{pre}")

由于模型准确率不是100%,因此上面预测结果和真实结果可能会不同. 如果我们多运行几次,必定会出现预测结果和真实结果相同的情况

下面我们来计算一下模型准确率到底是多少?

  1. with torch.no_grad():
  2.     y_pred = model(X_test)
  3.     # 上面计算出来的结果是0-1之间的数, 我们将数据进行四舍五入,得到与原表相同的情况
  4.     y_pred_cls = y_pred.round()
  5.     # 统计结果
  6.     acc = y_pred_cls.eq(Y_test).sum().numpy()/float(Y_test.shape[0])
  7.     print(f"准确率:{acc.item():.4f}")

我们利用测试数据,计算出了整个模型的预测准确率大概在90%左右,证明我们的模型可以很好的进行乳腺癌的诊断预测

小结

本节以乳腺癌的预测为例,引入了激活函数Sigmoid概念.建立了一个简单的非线性模型用于诊断患者是否患有乳腺癌. 其实, 这个案例已经是一个线性函数+激活函数的简单神经网络模型啦!