各位题友大家好！ 今天是 @负雪明烛 坚持日更的第 69 天。今天力扣上的每日一题是「1143. 最长公共子序列」。

解题思路

求两个数组或者字符串的最长公共子序列问题，肯定是要用动态规划的。

• 首先，区分两个概念：子序列可以是不连续的；子数组（子字符串）需要是连续的；
  - 另外，动态规划也是有套路的：单个数组或者字符串要用动态规划时，可以把动态规划 dp[i] 定义为 nums[0:i] 中想要求的结果；当两个数组或者字符串要用动态规划时，可以把动态规划定义成两维的 dp[i][j] ，其含义是在 A[0:i] 与 B[0:j] 之间匹配得到的想要的结果。

状态定义

比如对于本题而言，可以定义 dp[i][j] 表示 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。 （注：text1[0:i-1] 表示的是 text1 的 第 0 个元素到第 i - 1 个元素，两端都包含）
之所以 dp[i][j] 的定义不是 text1[0:i] 和 text2[0:j] ，是为了方便当 i = 0 或者 j = 0 的时候，dp[i][j]表示的为空字符串和另外一个字符串的匹配，这样 dp[i][j] 可以初始化为 0.

状态转移方程
知道状态定义之后，我们开始写状态转移方程。

• 当 text1[i - 1] == text2[j - 1] 时，说明两个子字符串的最后一位相等，所以最长公共子序列又增加了 1，所以 dp[i][j] = dp[i - 1][j - 1] + 1；举个例子，比如对于 ac 和 bc 而言，他们的最长公共子序列的长度等于 a 和 c 的最长公共子序列长度 0 + 1 = 1。
  - 当 text1[i - 1] != text2[j - 1] 时，说明两个子字符串的最后一位不相等，那么此时的状态 dp[i][j] 应该是 dp[i - 1][j] 和 dp[i][j - 1] 的最大值。举个例子，比如对于 ace 和 bc 而言，他们的最长公共子序列的长度等于 ① ace 和 b 的最长公共子序列长度0 与 ② ac 和 bc 的最长公共子序列长度1 的最大值，即 1。

状态的初始化

初始化就是要看当 i = 0 与 j = 0 时， dp[i][j] 应该取值为多少。
当 i = 0 时，dp[0][j] 表示的是 text1 中取空字符串 跟 text2 的最长公共子序列，结果肯定为 0.
当 j = 0 时，dp[i][0] 表示的是 text2 中取空字符串 跟 text1 的最长公共子序列，结果肯定为 0.
综上，当 i = 0 或者 j = 0 时，dp[i][j] 初始化为 0.

最终返回结果

由于 dp[i][j] 的含义是 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。我们最终希望求的是 text1 和 text2 的最长公共子序列。所以需要返回的结果是 i = len(text1) 并且 j = len(text2) 时的 dp[len(text1)][len(text2)]。

代码

经过上面的分析，我们可以得到下面的代码。

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        M, N = len(text1), len(text2)
        dp = [[0] * (N + 1) for _ in range(M + 1)]
        for i in range(1, M + 1):
            for j in range(1, N + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[M][N]

• 时间复杂度：$O(MN)$
• 空间复杂度：$O(MN)$

躲坑

如果你是用 python 刷题，需要注意 dp二维数组 的初始化，如果你的声明方式是下面这样，那么就是错的。

dp = [[0] * N ] * M

我们知道一维数组可以用 [0] * N 这种声明方式。但是二维数组不能用上面的声明方式，这会导致 dp 中的每行的列表是同一个 id，所以对其中一行的操作都会表现为每一行的操作，如下所示。

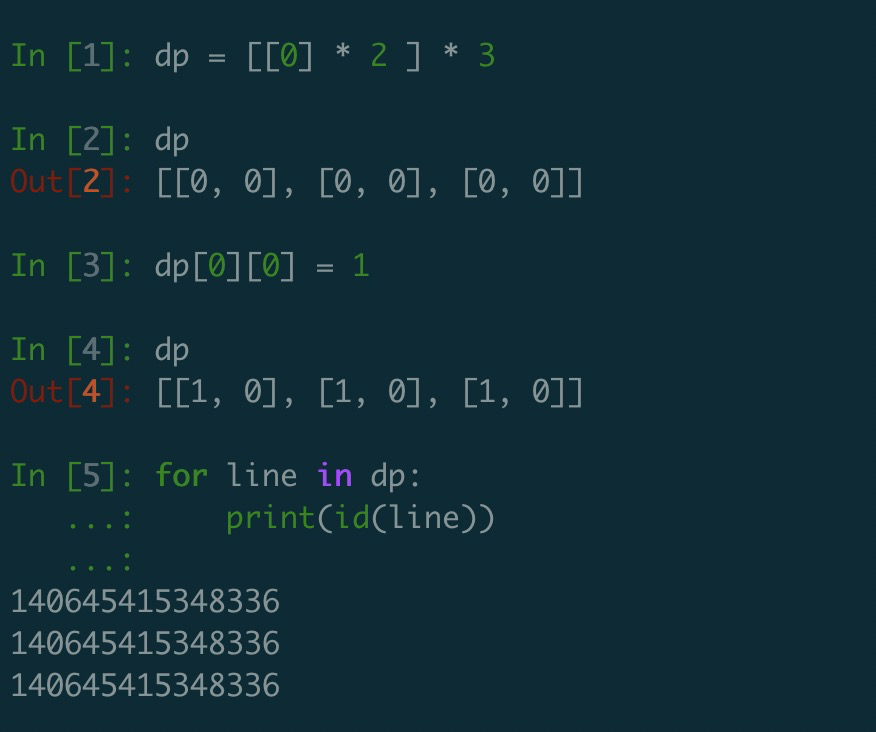
所以，在 Python 中声明二维数组的正确方式应该是：

dp = [[0] * N for _ in range(M)]

这里利用 for 循环生成每一行，则每一行都是全新的，那么就不会产生上面的问题。

刷题心得

坚持写题解两个多月，我对动态规划越来越熟悉了，发现基本上也都是套路。大家不要因为动态规划难，所以遇到动态规划就躲着走。刷题是补短板的过程，越是不懂，就越要学会和练习它。学习就是死磕自己的舒适区，希望大家不要沉醉于自己擅长的分类，要把每个分类的经典题目都做做，这样才能获得真正的进步。与君共勉。

参考资料：代码随想录

OK，以上就是 @负雪明烛 写的今天题解的全部内容了，如果你觉得有帮助的话，求赞、求关注、求收藏。如果有疑问的话，请在下面评论，我会及时解答。

关注我，你将不会错过我的精彩动画题解、面试题分享、组队刷题活动，进入主页 @负雪明烛 右侧有刷题组织，从此刷题不再孤单。

祝大家 AC 多多，Offer 多多！我们明天再见！