1.概念

数组是存放在连续内存空间上的相同类型数据的集合。
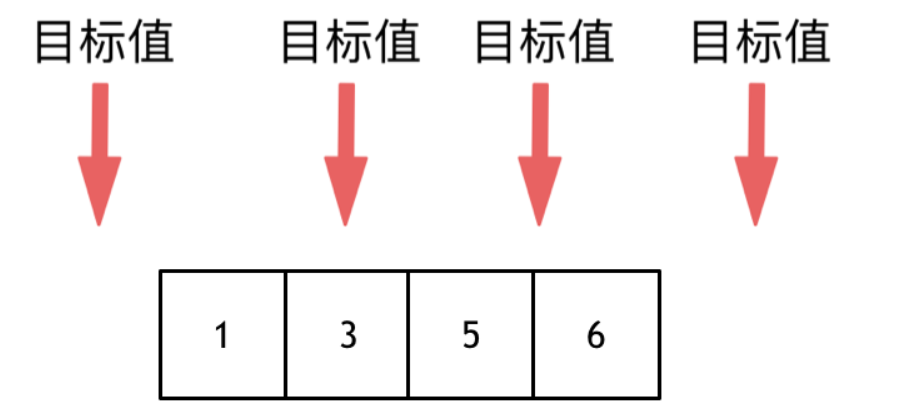
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
举一个字符数组的例子，如图所示：

需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：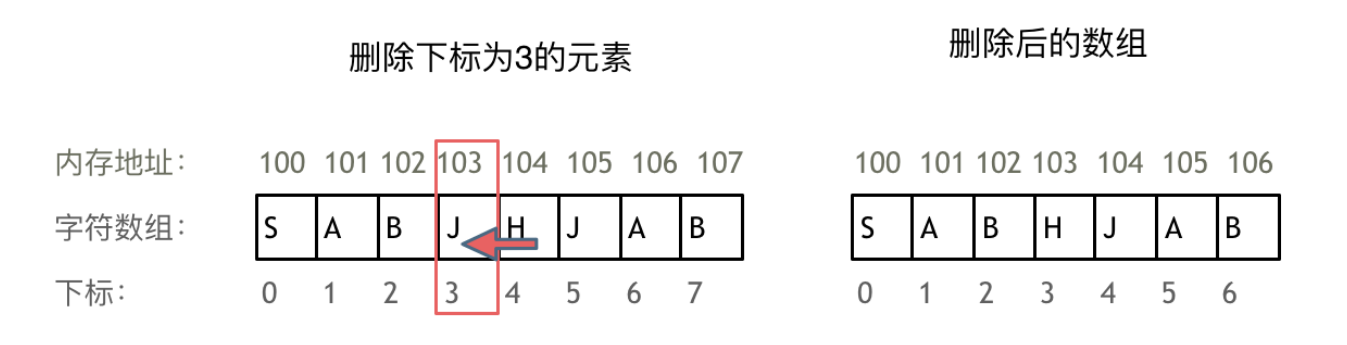

而且大家如果使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。
数组的元素是不能删的，只能覆盖。
那么二维数组直接上图，大家应该就知道怎么回事了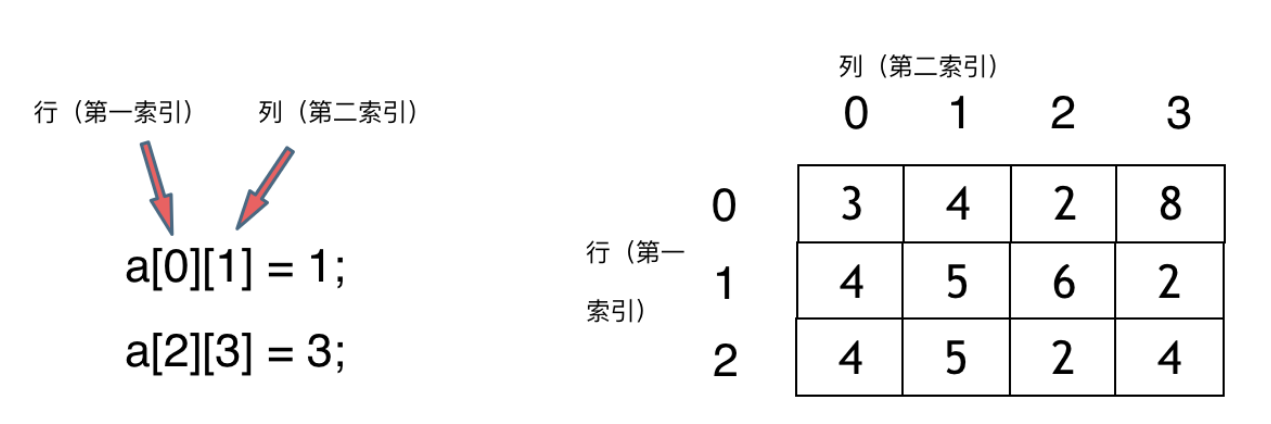

那么二维数组在内存的空间地址是连续的么？
不同编程语言的内存管理是不一样的，以C++为例，在C++中二维数组是连续分布的。
我们来做一个实验，C++测试代码如下：

void test_arr() {
    int array[2][3] = {
        {0, 1, 2},
        {3, 4, 5}
    };
    cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
    cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}
int main() {
    test_arr();
}
测试地址为：
0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834

注意地址为16进制，可以看出二维数组地址是连续一条线的。
一些录友可能看不懂内存地址，我就简单介绍一下， 0x7ffee4065820 与 0x7ffee4065824 差了一个4，就是4个字节，因为这是一个int型的数组，所以两个相邻数组元素地址差4个字节。
0x7ffee4065828 与 0x7ffee406582c 也是差了4个字节，在16进制里8 + 4 = c，c就是12。
如图：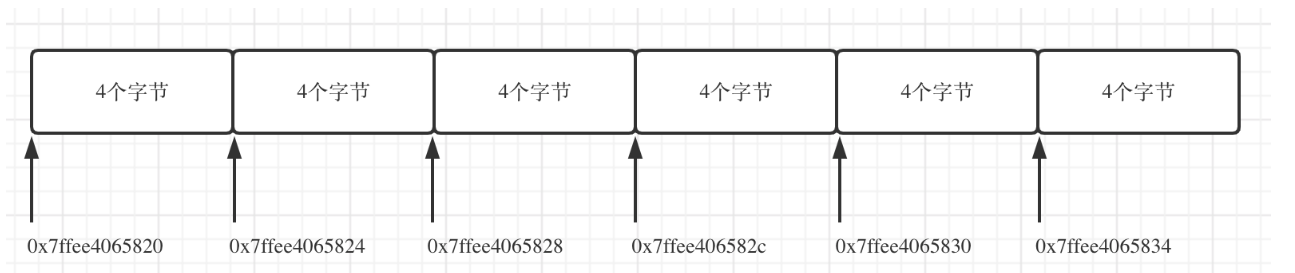

所以可以看出在C++中二维数组在地址空间上是连续的。

2. 二分法

704 二分查找

[

](https://leetcode-cn.com/problems/binary-search/)

思路

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。
二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？
大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。
写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。
下面我用这两种区间的定义分别讲解两种不同的二分写法。

写法一

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。
区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：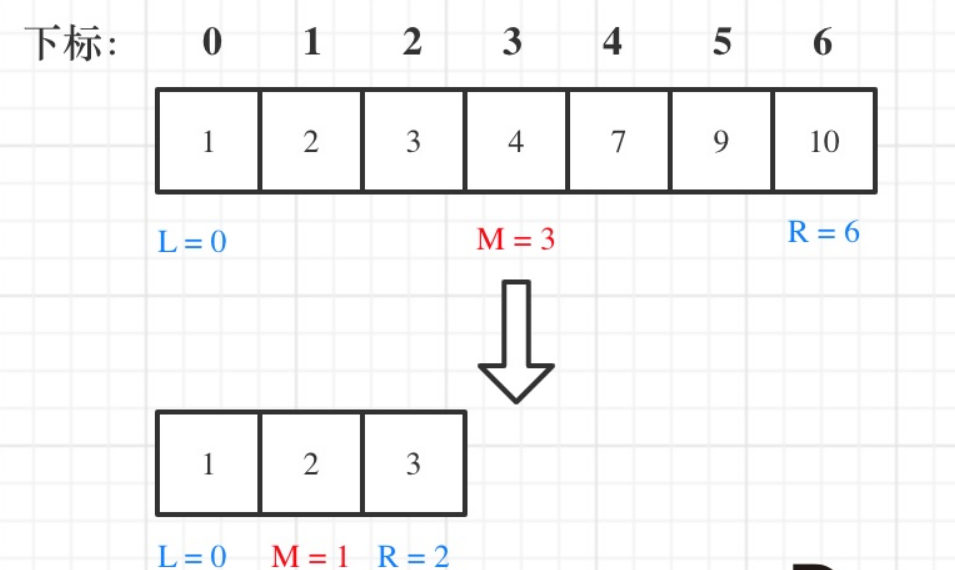

// 版本一
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

方法二

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。
有如下两点：

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）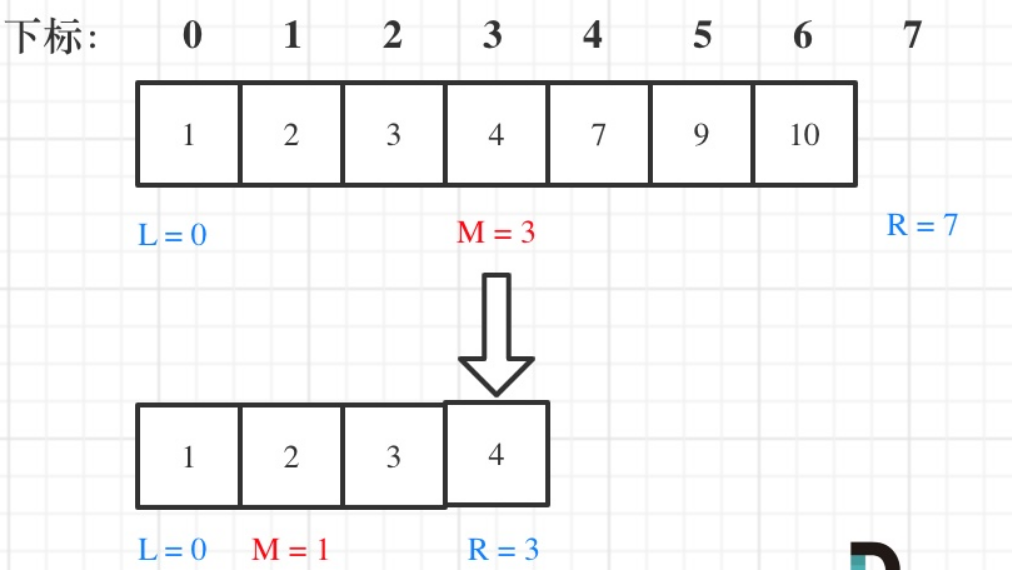

// 版本二
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

35. 搜索插入位置

思路

• 目标值在数组所有元素之前
• 目标值等于数组中某一个元素
• 目标值插入数组中的位置
• 目标值在数组所有元素之后

这四种情况确认清楚了，就可以尝试解题了。
接下来我将从暴力的解法和二分法来讲解此题，也借此好好讲一讲二分查找法。

暴力法

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        for (int i = 0; i < nums.size(); i++) {
        // 分别处理如下三种情况
        // 目标值在数组所有元素之前
        // 目标值等于数组中某一个元素
        // 目标值插入数组中的位置
            if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
                return i;
            }
        }
        // 目标值在数组所有元素之后的情况
        return nums.size(); // 如果target是最大的，或者 nums为空，则返回nums的长度
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

  二分法一（左闭右闭）

  class Solution {
  public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        //跳出循环时[right,left]
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， return right + 1
        return right + 1;  //或者return left;
    }
  };

二分法二（左闭右开）

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 定义target在左闭右开的区间里，[left, right)  target
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
            }
        }
        // left = right时跳出循环
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，return right 即可
        return right; //或者return left;
    }
};

34 在排序数组中查找元素的第一个和最后一个位置

思路

寻找target在数组里的左右边界，有如下三种情况：

• 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
• 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
• 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

这三种情况都考虑到，说明就想的很清楚了。
接下来，在去寻找左边界，和右边界了。

二分法一（左闭右闭）

寻找右边界时，等号赋给nums[middle] < target,即nums[middle] <= target，此时left = mid+1,跳出循环时，left在最右边的target的右边即右边界+1
寻找左边界时，等号赋给nums[middle] > target,即nums[middle] >= target，此时right= mid -1 ,跳出循环时，right在最左边的target的左边即左边界-1

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int leftBorder = getLeftBorder(nums, target);
        int rightBorder = getRightBorder(nums, target);
        // 情况一
        if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
        // 情况三
        if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
        // 情况二
        return {-1, -1};
    }
private:
     int getRightBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
        while (left <= right) {
            int middle = left + ((right - left) / 2);
            if (nums[middle] > target) {
                right = middle - 1;
            } else { // 寻找右边界，nums[middle] == target的时候更新left
                left = middle + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }
    int getLeftBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
        while (left <= right) {
            int middle = left + ((right - left) / 2);
            if (nums[middle] >= target) { // 寻找左边界，nums[middle] == target的时候更新right
                right = middle - 1;
                leftBorder = right;
            } else {
                left = middle + 1;
            }
        }
        return leftBorder;
    }
};

二分法二（左闭右开）

寻找右边界时，等号赋给nums[middle] < target,即nums[middle] <= target，此时left = mid+1,跳出循环时，left在最右边的target的右边即右边界+1
寻找左边界时，等号赋给nums[middle] > target,即nums[middle] >= target，此时right= mid -1 ,跳出循环时，right在最左边的target即左边界

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int rightboard = getright(nums,target);
        int leftboard = getleft(nums,target);
        if(leftboard==-2||rightboard==-2) return {-1,-1};
        if(rightboard-leftboard>0) return {leftboard,rightboard-1};
        return {-1,-1};

    }
    int getright(vector<int>& nums, int target)
    {   
        int left = 0,right =nums.size();
        int rightboard = -2;
        while(left<right)
        {
            int mid = left+(right-left)/2;
            if(nums[mid]>target)
                right = mid;
            else
            {
                left = mid+1;
                rightboard = left;
            }
        }
        return rightboard;
    }
    int getleft(vector<int>& nums, int target)
    {   
        int left = 0,right =nums.size();
        int leftboard = -2;
        while(left<right)
        {
            int mid = left+(right-left)/2;
            if(nums[mid]>=target)
            {
                right = mid;
                leftboard = right;
            }
            else
                left = mid+1;
        }
        return leftboard;
    }
};

3. 双指针

27.移除元素

快慢指针

用慢指针记录不等于val的数字位置，快指针遍历数组
当快指针所指数字等于val时，快指针+1，慢指针不动，直到快指针所指数字不等于val，将快指针所指数字的值将慢指针所指的值覆盖，同时快慢指针都+1;

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int low = 0;
        for(int i = 0;i<nums.size();i++)
        {
            if(nums[i] != val)
            {
                nums[low] = nums[i];
                low++;
            }
        }
        return low;
    }
};

双向指针

左右指针遍历数组，当left>right时遍历结束，此时left指针所指的为最终数组末尾的下一个元素。
左指针用于寻找第一个等于val的数字，右指针用于寻找第一个不等于val的数字，然后将右指针数字覆盖至左指针所指数字。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
       int left = 0;
       int right = nums.size()-1;
       while(left<=right)
       {
            while(left<=right && nums[left] != val)
                left++;
            while(left<=right && nums[right] == val)
                right--;
            if(left<=right)
            {
                nums[left++] = nums[right--];
            }
       }
       return left;
    }
};

26. 删除有序数组中的重复项

法一:

同27

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int slow = 0;
        for(int i = 0;i<nums.size();i++)
        {
            if(nums[i] != nums[slow])
                nums[++slow] = nums[i];
        }
        return slow+1;
    }
};

法二：

慢指针用于记录有效数组的末尾，快指针用于遍历数组，循环找到同个数字的末尾，并将数字赋给slow+1位置；

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int slow = 0,fast = 0;
        while(fast<nums.size())
        {
            int temp = nums[fast];
            while(fast<nums.size() && nums[fast]== temp)
                fast++;
            if(fast<nums.size())
                nums[++slow] = nums[fast];
        }
        return slow+1;
    }
};

977. 有序数组的平方

数组其实是有序的， 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。
此时可以考虑双指针法了，i指向起始位置，j指向终止位置。
定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。
如果A[i] A[i] < A[j] A[j] 那么result[k—] = A[j] A[j]; 。
如果A[i] A[i] >= A[j] A[j] 那么result[k—] = A[i] A[i]; 。

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> result(nums.size());
        int k = nums.size()-1;
        for(int i=0,j=nums.size()-1;i<=j;)
        {
            if(nums[i]*nums[i]>nums[j]*nums[j])
            {
                result[k--] = nums[i]*nums[i];
                i++;
            }
            else
            {
                result[k--] = nums[j]*nums[j];
                j--;
            }
        }
        return result;
    }
};

209.长度最小的子数组

滑动窗口

快指针维护窗口的右边界，慢指针维护窗口的左边界。当窗口内和小于target时，fast++扩大右边界，反之，slow++，缩小左边界。
result用于记录最小数组长度，初始化为INA_MAX

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int len = 0;
        int slow = 0,fast =0;
        int sum = 0;
        int result = INT_MAX;
        while(fast<nums.size())
        {
            sum += nums[fast];
            while(sum>=target)
            {
                len = fast-slow+1;
                result = min(result,len);
                sum -= nums[slow];
                slow++;
            }
            fast++; 
        }
        return result==INT_MAX?0:result;
    }
};

59.螺旋矩阵

因为要添加的元素为连续数字，循环终止条件可设为num<n*n.

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int top=0,down=n-1,left = 0, right = n-1;
        vector<vector<int>> result(n,vector<int>(n));
        int num = 1;
        while(num<=n*n)
        {
            for(int i = left; i<=right;i++)
                result[top][i] = num++;
            top++;
            for(int i = top; i<=down;i++)
                result[i][right] = num++;
            right--;
            for(int i = right; i>=left;i--)
                result[down][i] = num++;
            down--;
            for(int i = down; i>=top;i--)
                result[i][left] = num++;
            left++;
        }
        return result;
    }
};