原文网址
树 是一种经常用到的数据结构，用来模拟具有树状结构性质的数据集合。
树里的每一个节点有一个值和一个包含所有子节点的列表。从图的观点来看，树也可视为一个拥有N 个节点和N-1 条边的一个有向无环图。
二叉树是一种更为典型的树状结构。如它名字所描述的那样，二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。
完成后，你将：

  1. 掌握树和二叉树的概念
  2. 熟悉不同的遍历方法
  3. 运用递归解决二叉树相关题目

1.树的遍历

1.1 前序遍历

前序遍历首先访问根节点，然后遍历左子树，最后遍历右子树。

image.png

1.2 中序遍历

中序遍历是先遍历左子树，然后访问根节点，然后遍历右子树。
通常来说，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。 我们将在另一张卡片（数据结构介绍 – 二叉搜索树）中再次提及。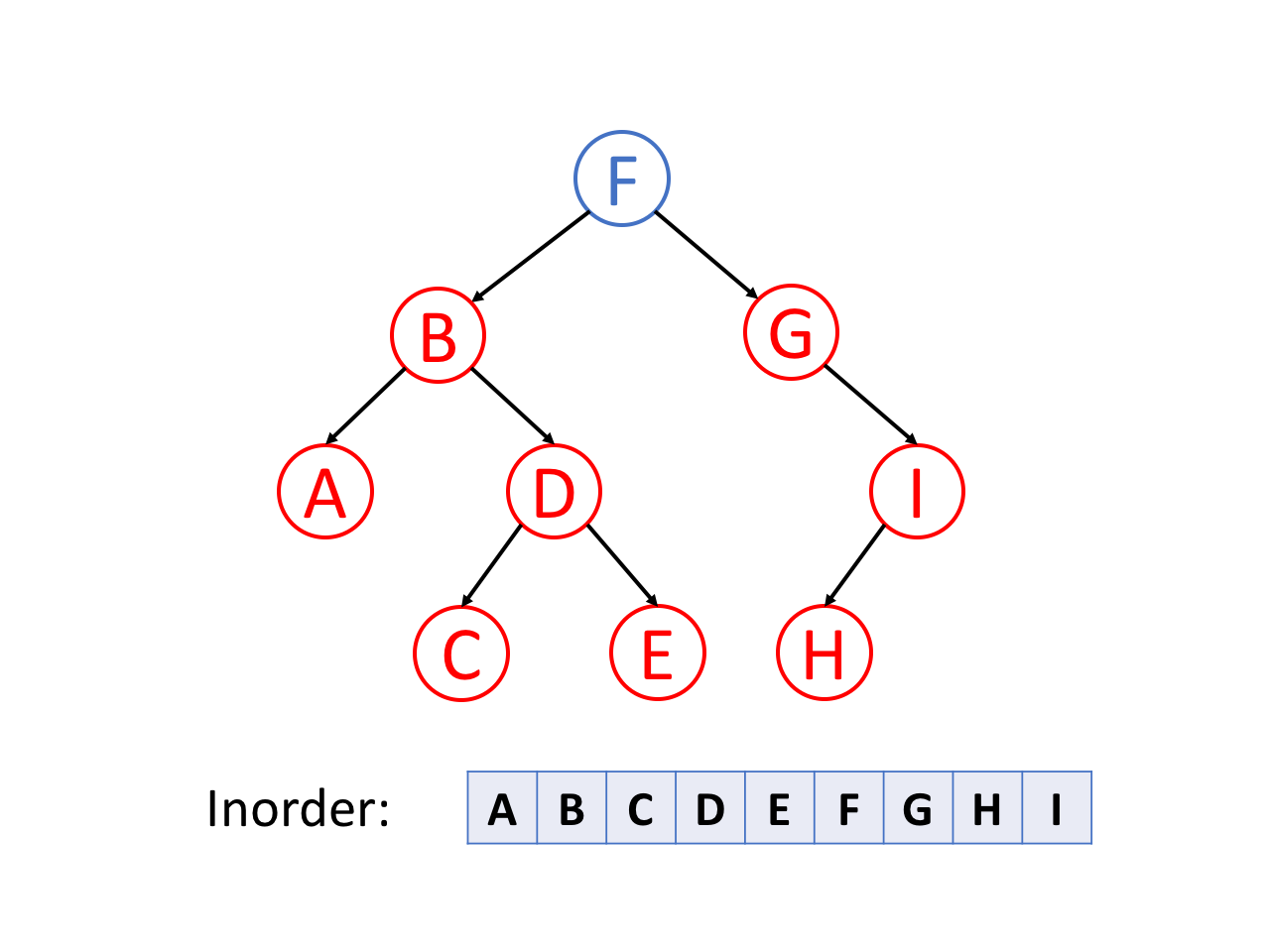
image.png

1.3 后序遍历

后序遍历是先遍历左子树，然后遍历右子树，最后访问树的根节点。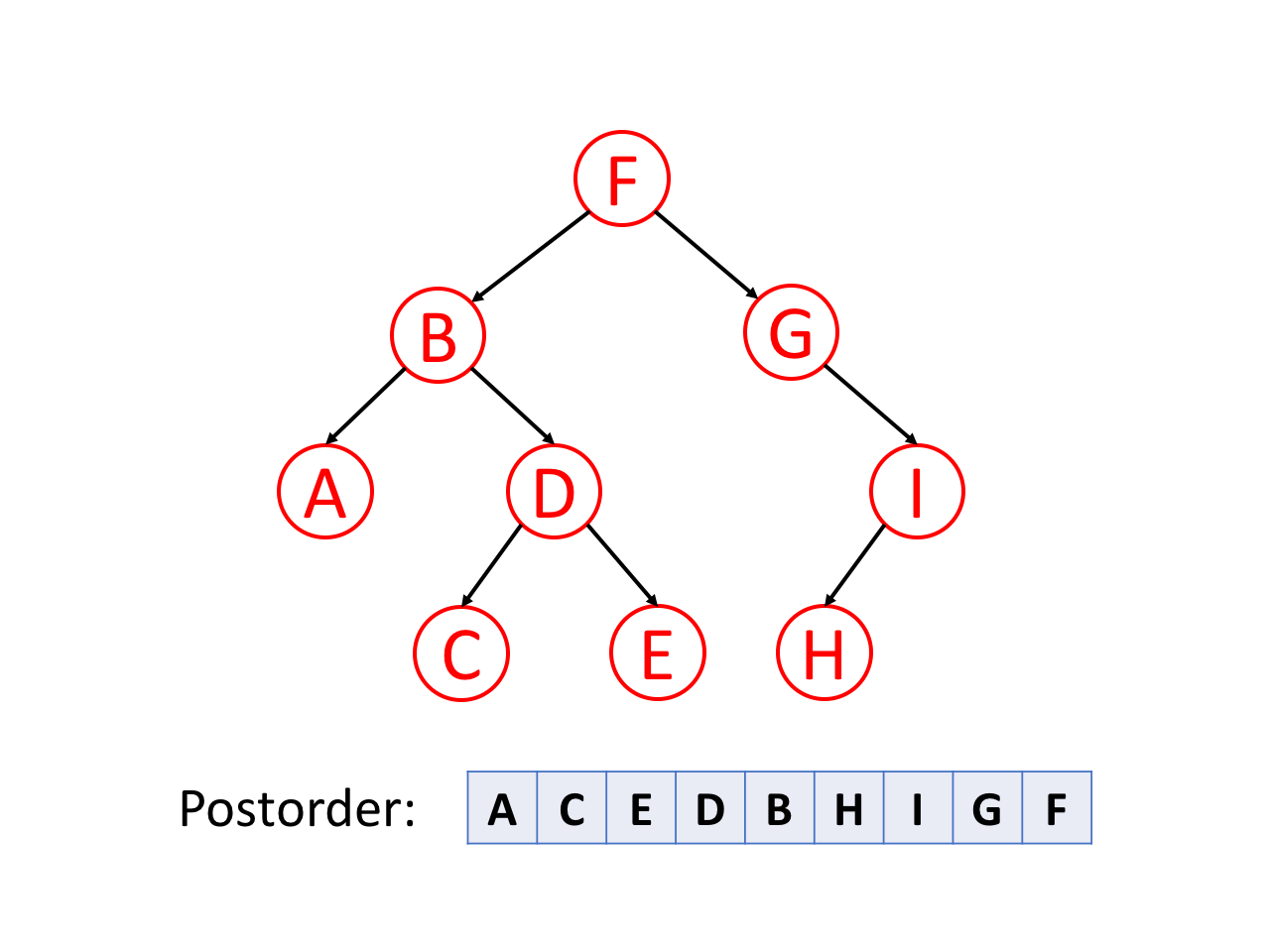
image.png

当你删除树中的节点时，删除过程将按照后序遍历的顺序进行。 也就是说，当你删除一个节点时，你将首先删除它的左节点和它的右边的节点，然后再删除节点本身。
另外，后序在数学表达中被广泛使用。 编写程序来解析后缀表示法更为容易。 这里是一个例子：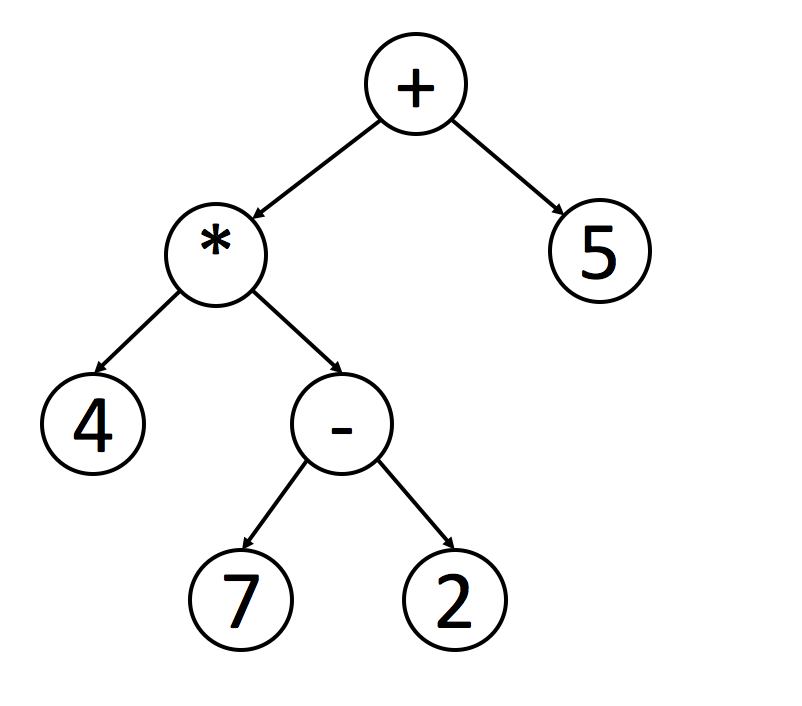
image.png
您可以使用中序遍历轻松找出原始表达式。 但是程序处理这个表达式时并不容易，因为你必须检查操作的优先级。

如果你想对这棵树进行后序遍历，使用栈来处理表达式会变得更加容易。 每遇到一个操作符，就可以从栈中弹出栈顶的两个元素，计算并将结果返回到栈中。