322. 零钱兑换

  1. 确定dp数组以及下标的含义

dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

  1. 确定递推公式

得到dp[j]（考虑coins[i]），只有一个来源，dp[j - coins[i]]（没有考虑coins[i]）。
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

  1. dp数组如何初始化

首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;
其他下标对应的数值呢？
考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
代码如下：

  1. vector<int> dp(amount + 1, INT_MAX);
  2. dp[0] = 0;
  1. 确定遍历顺序

本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。
所以本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的！
那么我采用coins放在外循环，target在内循环的方式。
本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序

  1. 举例推导dp数组

以输入：coins = [1, 2, 5], amount = 5为例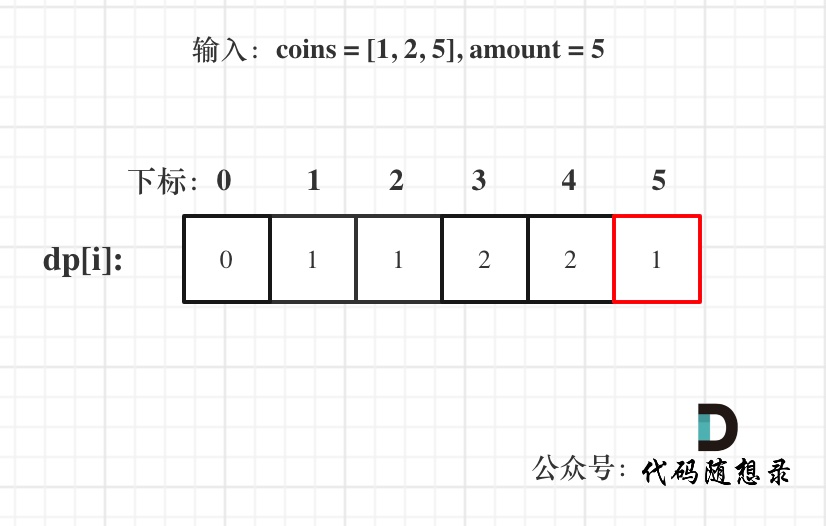
image.png
dp[amount]为最终结果。

代码

  1. class Solution {
  2. public:
  3.     int coinChange(vector<int>& coins, int amount) {
  4.         vector<int> dp(amount+1,INT_MAX);
  5.         dp[0]=0;
  6.         for(int coin:coins)
  7.             for(int j=coin;j<=amount;j++)
  8.                 if(dp[j-coin] != INT_MAX)
  9.                     dp[j] = min(dp[j],dp[j-coin]+1);
  10.         return dp[amount]==INT_MAX?-1:dp[amount];
  11.     }
  12. };