516. 最长回文子序列

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

  1. 转移方程

    如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;
    如图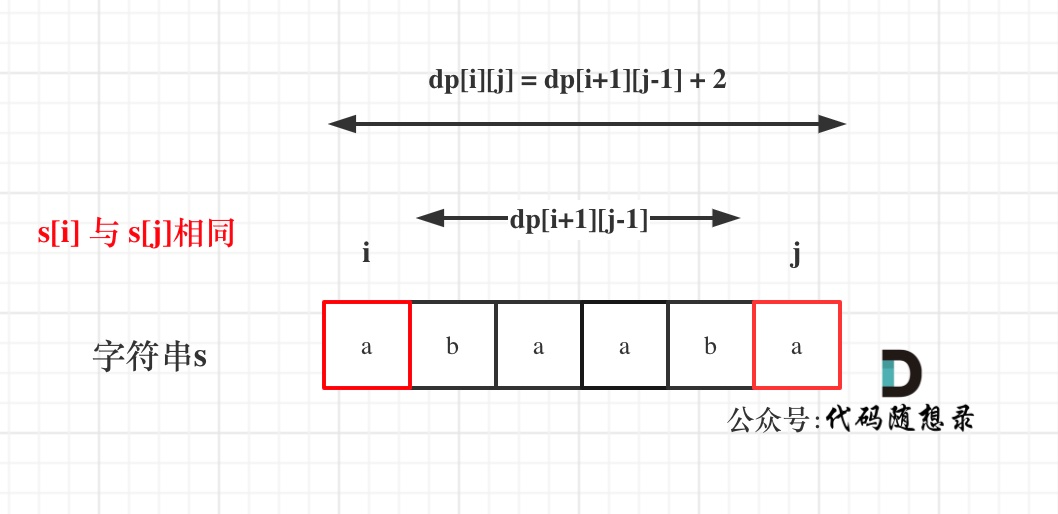： image.png

如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

  • 加入s[j]的回文子序列长度为dp[i + 1][j]。
  • 加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);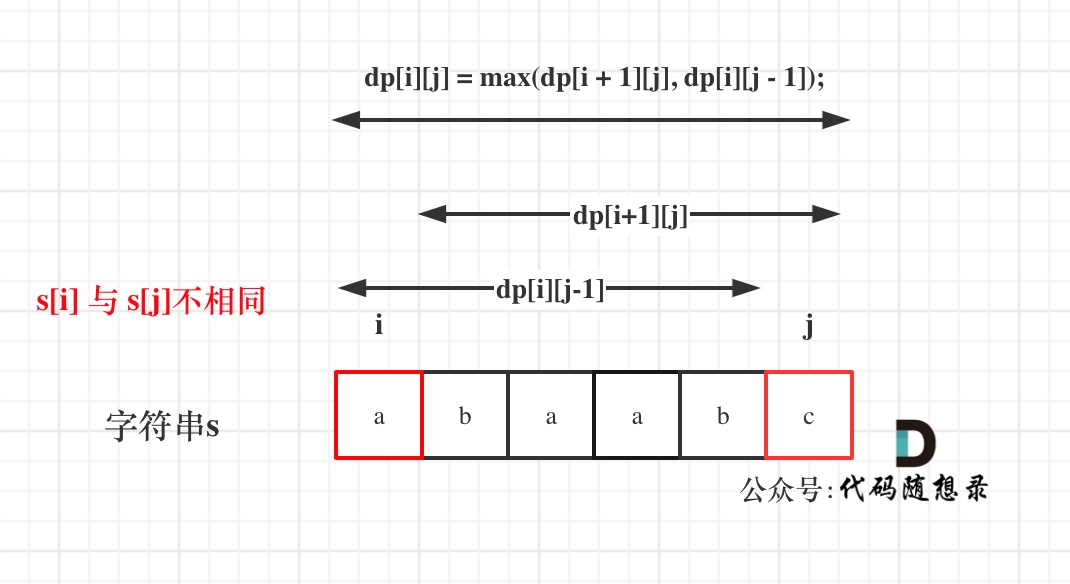
image.png

  1. if (s[i] == s[j]) {
  2.     dp[i][j] = dp[i + 1][j - 1] + 2;
  3. } else {
  4.     dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
  5. }
  1. 初始化

首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。

  1. vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
  2. for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
  1. 遍历顺序

从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出，dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j]，
也就是从矩阵的角度来说，dp[i][j] 下一行的数据。 所以遍历i的时候一定要从下到上遍历，这样才能保证，下一行的数据是经过计算的。
递推公式：dp[i][j] = dp[i + 1][j - 1] + 2，dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 分别对应着下图中的红色箭头方向，如图：

  1. for (int i = s.size() - 1; i >= 0; i--) {
  2.     for (int j = i + 1; j < s.size(); j++) {
  3.         if (s[i] == s[j]) {
  4.             dp[i][j] = dp[i + 1][j - 1] + 2;
  5.         } else {
  6.             dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
  7.         }
  8.     }
  9. }

代码

  1. class Solution {
  2. public:
  3.     int longestPalindromeSubseq(string s) {
  4.         vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
  5.         for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
  6.         for (int i = s.size() - 1; i >= 0; i--) {
  7.             for (int j = i + 1; j < s.size(); j++) {
  8.                 if (s[i] == s[j]) {
  9.                     dp[i][j] = dp[i + 1][j - 1] + 2;
  10.                 } else {
  11.                     dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
  12.                 }
  13.             }
  14.         }
  15.         return dp[0][s.size() - 1];
  16.     }
  17. };