42. 接雨水

双指针

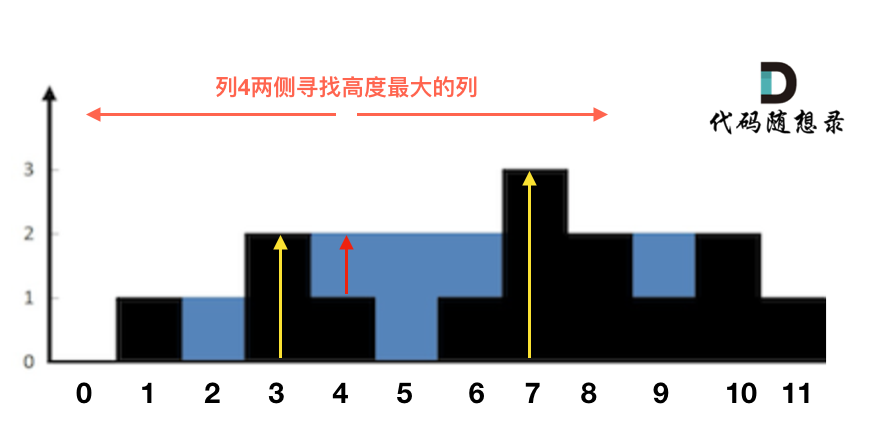
按列求雨水数量，寻找当前列左右的最大高度，如何取左右高度中较小的高度-当前列高度

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        for (int i = 0; i < height.size(); i++) {
            // 第一个柱子和最后一个柱子不接雨水
            if (i == 0 || i == height.size() - 1) continue;
            int rHeight = height[i]; // 记录右边柱子的最高高度
            int lHeight = height[i]; // 记录左边柱子的最高高度
            for (int r = i + 1; r < height.size(); r++) {
                if (height[r] > rHeight) rHeight = height[r];
            }
            for (int l = i - 1; l >= 0; l--) {
                if (height[l] > lHeight) lHeight = height[l];
            }
            int h = min(lHeight, rHeight) - height[i];
            if (h > 0) sum += h;
        }
        return sum;
    }
};

上述因为重复寻找最大高度，所以会超时，使用两个变量来记录左右的最大高度

class Solution {
public:
    int trap(vector<int>& height)
    {
        int left = 0, right = height.size() - 1;
        int ans = 0;
        int left_max = 0, right_max = 0;
        while (left < right) {
            //当左边高度小于右边高度时，当前列的水滴数与坐边的最大高度有关
            if (height[left] < height[right]) {
                //如果当前列的高度大于左边的最大高度，更新左边的最大高度
                //反之，计算水滴数相当于min(lHeight, rHeight) - height[i]
                height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
                ++left;
            }
            else {
                height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
                --right;
            }
        }
        return ans;
    }
};

动态规划

转移方程
当前位置，左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
即从左向右遍历：maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历：maxRight[i] = max(height[i], maxRight[i + 1]);

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        vector<int> maxLeft(height.size(), 0);
        vector<int> maxRight(height.size(), 0);
        int size = maxRight.size();
        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i < size; i++) {
            maxLeft[i] = max(height[i], maxLeft[i - 1]);
        }
        // 记录每个柱子右边柱子最大高度
        maxRight[size - 1] = height[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            maxRight[i] = max(height[i], maxRight[i + 1]);
        }
        // 求和
        int sum = 0;
        for (int i = 0; i < size; i++) {
            int count = min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
};

单调栈

1. 当前列高度小于等于栈顶高度时，将当前高度进栈
2. 反之将当前列高度、栈顶元素和栈顶上一个元素形成凹槽，计算雨水

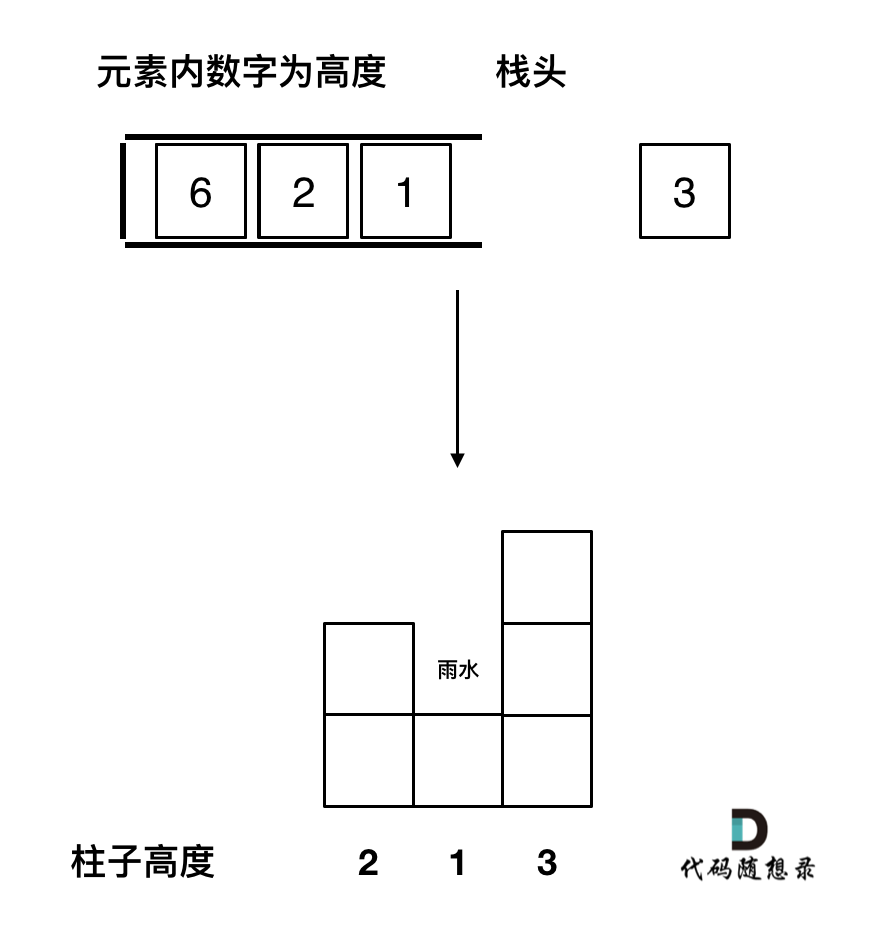
class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        st.push(0);
        int sum = 0;
        for (int i = 1; i < height.size(); i++) {
            while (!st.empty() && height[i] > height[st.top()]) {
                int mid = st.top();
                st.pop();
                if (!st.empty()) {
                    int h = min(height[st.top()], height[i]) - height[mid];
                    int w = i - st.top() - 1;
                    sum += h * w;
                }
            }
            st.push(i);
        }
        return sum;
    }
};