84. 柱状图中最大的矩形

双指针

遍历列，然后向左向右分别找到第一个小于当前高度的索引
计算宽度为right-left-1，（表示不包含小于当前列高度的宽度）

  1. class Solution {
  2. public:
  3.     int largestRectangleArea(vector<int>& heights) {
  4.         int sum = 0;
  5.         for (int i = 0; i < heights.size(); i++) {
  6.             int left = i;
  7.             int right = i;
  8.             for (; left >= 0; left--) {
  9.                 if (heights[left] < heights[i]) break;
  10.             }
  11.             for (; right < heights.size(); right++) {
  12.                 if (heights[right] < heights[i]) break;
  13.             }
  14.             int w = right - left - 1;
  15.             int h = heights[i];
  16.             sum = max(sum, w * h);
  17.         }
  18.         return sum;
  19.     }
  20. };

动态规划

  1. class Solution {
  2. public:
  3.     int largestRectangleArea(vector<int>& heights) {
  4.         vector<int> minLeftIndex(heights.size());
  5.         vector<int> minRightIndex(heights.size());
  6.         int size = heights.size();
  8.         // 记录每个柱子 左边第一个小于该柱子的下标
  9.         minLeftIndex[0] = -1; // 注意这里初始化，防止下面while死循环
  10.         for (int i = 1; i < size; i++) {
  11.             int t = i - 1;
  12.             // 这里不是用if，而是不断向左寻找的过程
  13.             while (t >= 0 && heights[t] >= heights[i]) 
  14.                 //此处的minLeftIndex[t]即相当于minLeftIndex[i-1]
  15.                 //要通过while循环判断minLeftIndex[i-1]记录的高度是否小于当前高度
  16.                 //若还不小于，需要再向左查找
  17.                 t = minLeftIndex[t];
  18.             minLeftIndex[i] = t;
  19.         }
  20.         // 记录每个柱子 右边第一个小于该柱子的下标
  21.         minRightIndex[size - 1] = size; // 注意这里初始化，防止下面while死循环
  22.         for (int i = size - 2; i >= 0; i--) {
  23.             int t = i + 1;
  24.             // 这里不是用if，而是不断向右寻找的过程
  25.             while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
  26.             minRightIndex[i] = t;
  27.         }
  28.         // 求和
  29.         int result = 0;
  30.         for (int i = 0; i < size; i++) {
  31.             int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
  32.             result = max(sum, result);
  33.         }
  34.         return result;
  35.     }
  36. };

单调栈

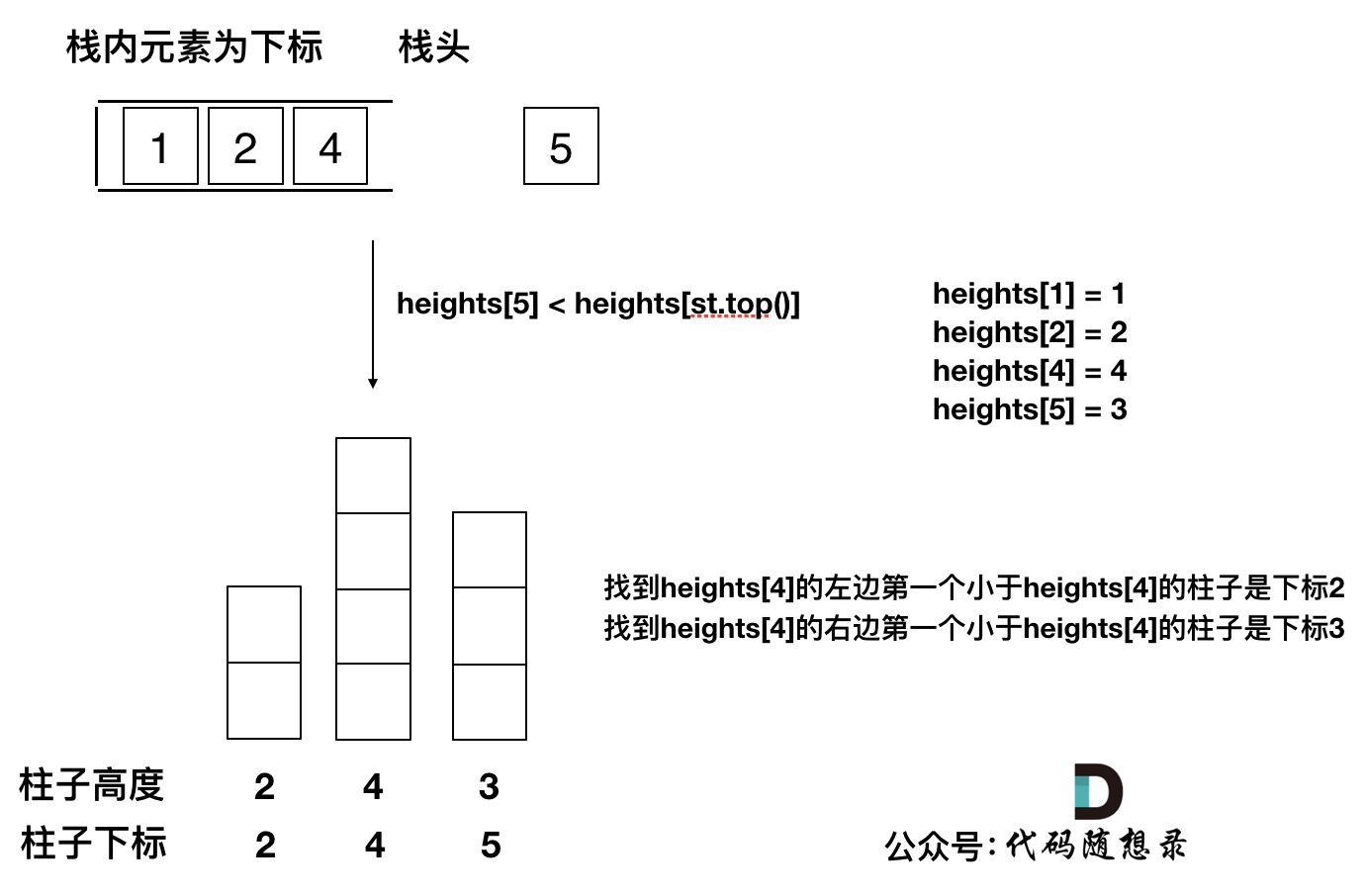
image.png

维护一个单调递增的栈
当遇到当前高度小于栈顶高度时，说明找到了右边第一个小于栈顶高度的柱子
同时因为是单调递增的，所以栈顶元素前一个柱子的高度一定小于栈顶高度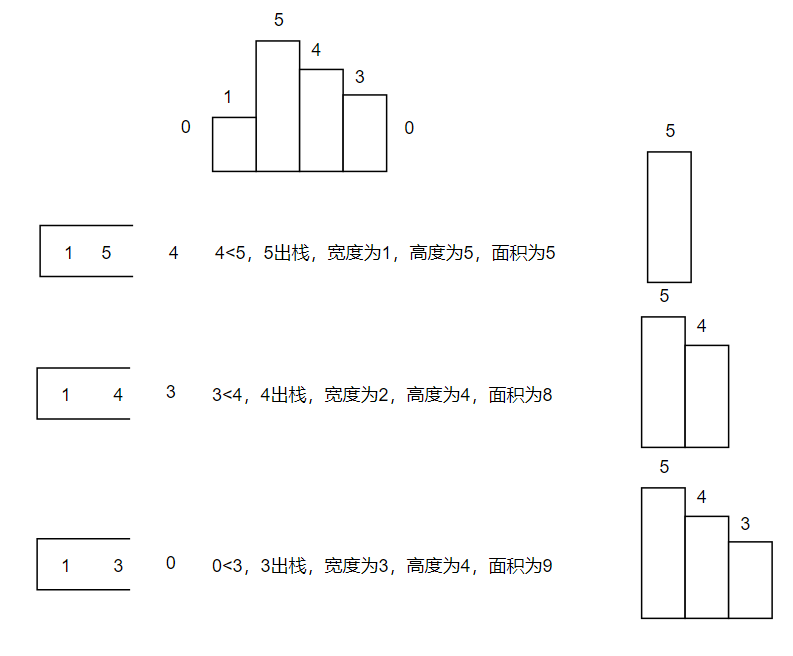
image.png

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st;
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0);
        int result = 0;
        for (int i = 1; i < heights.size(); i++) {
            while (heights[i] < heights[st.top()]) {
                int mid = st.top();
                st.pop();
                int w = i - st.top() - 1;
                int h = heights[mid];
                result = max(result, w * h);
            }
            st.push(i);
        }
        return result;
    }
};