874. 模拟行走机器人

机器人在一个无限大小的网格上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令：

• -2：向左转 90 度
• -1：向右转 90 度
• 1 <= x <= 9：向前移动 x 个单位长度

在网格上有一些格子被视为障碍物。 第 i 个障碍物位于网格点 (obstacles[i][0], obstacles[i][1]) 机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，但仍然可以继续该路线的其余部分。 返回从原点到机器人所有经过的路径点（坐标为整数）的最大欧式距离的平方。 示例 1：

输入: commands = [4,-1,3], obstacles = []
输出: 25
解释: 机器人将会到达 (3, 4)

示例 2：

输入: commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出: 65
解释: 机器人在左转走到 (1, 8) 之前将被困在 (1, 4) 处

提示：

1. 0 <= commands.length <= 10000
2. 0 <= obstacles.length <= 10000
3. -30000 <= obstacle[i][0] <= 30000
4. -30000 <= obstacle[i][1] <= 30000
5. 答案保证小于 2 ^ 31

解题思路

先把题目搞明白，解释题目中示例2的意思

示例 2：
输入: commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出: 65
解释: 机器人在左转走到 (1, 8) 之前将被困在 (1, 4) 处

输入：commands和obstacles，其中 obstacles = [[2,4]] 的意思是坐标点(2,4)代表障碍物的坐标
输出：机器人所经过的每个坐标点(x,y)到原点的欧式距离的平方的最大值
欧式距离:
欧式距离的平方: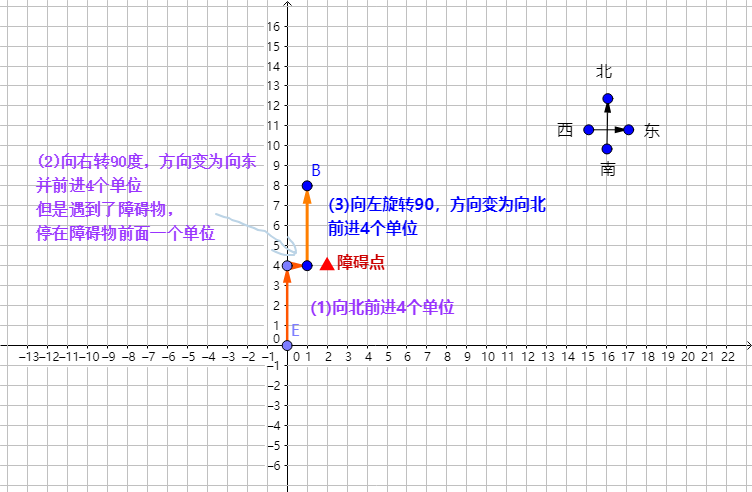

如上图所示：

机器人初始位置为坐标点(0,0)，初始方向为向北
读取第一个指令为4，沿着当前方向“北”，向前走4个单位，停在坐标点(0,4)
读取第二个指令-1，该指令表示“向右转90度”，那么机器人就由原来的“北”右转90度之后方向变为“东”
读取第三个指令4，沿着当前方向“东”，向前走4个单位，但是发现坐标点(2,4)是一个障碍物，不能跨越障碍物，
只能停留在障碍物前面一个单位，即坐标点(1,4)
读取第四个指令-2，该指令表示“向左转90度”，那么机器人就由原来的“东”左转90度之后方向变为“北”
读取第五个指令4，沿着当前方向“北”，向前走4个单位，停在坐标点(1,8)

65怎么得来的？ 机器人所经过的这些点中，(1,8)计算出的欧式距离的平方最大，为

代码实现

参考官方题解，可以提交通过，注意注释

   /*
命令：
    -2：向左转 90 度
    -1：向右转 90 度
    1 <= x <= 9：向前移动 x 个单位长度

    obstacles = [[2,4]] 的意思是坐标点(2,4)代表障碍物的坐标

    每一步怎么走？ 走( direx[i], direy[i] )，加上当前坐标后为 (curx,cury) + ( direx[i], direy[i] )
    direx[],direy[] 要竖着对齐看
    向北，坐标轴上x不动，y+1
    向东，坐标轴上x+1，y不动
    向南，坐标轴上x不动，y-1
    向西，坐标轴上x-1，y不动
*/
class Solution {
public:
    int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
        int direx[] = {0,1,0,-1};
        int direy[] = {1,0,-1,0};
        int curx=0,cury=0;
        int curdire = 0;
        int comLen = commands.size();
        int ans = 0;
        set<pair<int, int>> obstacleSet;
        for(int i=0;i<obstacles.size();i++)
            obstacleSet.insert(make_pair(obstacles[i][0], obstacles[i][1]));

        for(int i=0;i<comLen;i++){
            if(commands[i] == -1){  // -1：向右转 90 度
                curdire = (curdire + 1) % 4;
            }else if(commands[i] == -2){  // -2：向左转 90 度
                 curdire = (curdire + 3) % 4;
            }else{  //  1 <= x <= 9：向前移动 x 个单位长度
                for(int j=0;j<commands[i];j++){
                    //试图走出一步，并判断是否遇到了障碍物，
                    int nx = curx + direx[curdire];
                    int ny = cury + direy[curdire];
                    //当前坐标不是障碍点，计算并与存储的最大欧式距离的平方做比较
                    if (obstacleSet.find(make_pair(nx, ny)) == obstacleSet.end()) {
                        curx = nx;
                        cury = ny;
                        ans = max(ans, curx*curx + cury*cury);
                    }else{
                        //是障碍点，被挡住了，停留，只能等待下一个指令，那可以跳出当前指令了
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

注：
set和unordered_set底层分别是用红黑树和哈希表实现的。
unordered_set不能用来保存pair，但是set可以。
因为unordered_set是基于哈希的，而C++并没有给pair事先写好哈希方法。
set是基于比较的树结构，所以pair里的数据结构只要都支持比较就能储存。