45. 跳跃游戏 II

45. 跳跃游戏 II

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。 示例: 输入: [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置，跳 2 步，然后跳 3 步到达数组的最后一个位置。 说明: 假设你总是可以到达数组的最后一个位置。

解题思路

思路1（超时）

一开始想的第一个版本是用一个数组 记录跳到每个位置的最小步数。（有点动态规划的意思）
即： 代表了能跳到位置 的最小步数
初始时

然后从头开始遍历数组，动态更新

//顺序遍历数组的每个位置
for(int i=0;i<n;i++) {
    //遍历从nums[i]能跳跃的位置，更新其最小步数
    for(int j=1;j<=nums[i];j++) {
        if(i+j < n)
           jumpNums[i+j] = min(jumpNums[i+j],jumpNums[i]+1);
    }
}

最后答案返回的就是
很明显，时间复杂度 ，空间复杂度

思路2

参考 官方题解 参考 详细通俗的思路分析，多解法 还是不是很理解 step在更新边界得时候，step++

使用「贪心」地进行正向查找，每次找到可到达的最远位置，就可以在线性时间内得到最少的跳跃次数。
如下图，开始的位置是 2，可跳的范围是橙色的。然后因为 3 可以跳的更远，所以跳到 3 的位置。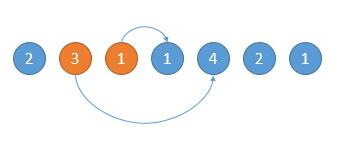

如下图，然后现在的位置就是 3 了，能跳的范围是橙色的，然后因为 4 可以跳的更远，所以下次跳到 4 的位置。

代码上，我们用 end 表示当前能跳的边界(可跳范围)，对于上边第一个图的橙色 1，第二个图中就是橙色的 4。
遍历数组的时候，到了边界，我们就重新更新新的边界。同时步数加一

过程解析：
最开始遍历 i = 0, end = 0，因此 step 会进行 step ++，我们可以认为，这是开始起跳，因为必定会落下，因此跳跃次数 + 1。
而 nums[0] 这个数限制了你只能在落脚在某个范围内，假如 nums[0] = 4，那么你只能选择落脚在 [1, 4] 位置，而如果到了边界，那么肯定是一次新的起跳，因此次数需要再 + 1。
从位置 0 开始起跳，你落脚的必定是 [1, 4] 位置中能够跳得更远的， 因为根据贪心思想，这样做能够尽可能的减少跳跃次数，因为更加接近最后一个位置。
而在这个过程遍历 [1, 4] 过程中一直记录着最远位置 k，因此当到达边界的时候，将 end 更新为 k

具体实现

1. 顺序遍历数组， 保存目前能跳到的最远距离。

遍历的过程通过 来实时更新

1. 使用 end 记为边界。我们从左到右遍历数组，到达边界时，更新边界并将跳跃次数增加 1。即当 时 ，更新 ，并且

时间复杂度 ，空间复杂度

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        int maxPos = 0;//当前最远可以到达的位置
        int step = 0;
        int end  = 0;//竖立一个标志，到这里就需要跳，步数加一
        for(int i=0;i < n-1;i++) {
            //能到达位置 i
           if( maxPos >= i) {
               maxPos = max(maxPos,i + nums[i]);//若 i + nums[i] > maxPos,则从位置 i 跳更远
               //第一次起跳 或 到达跳跃的边界
               if( i == end) {//到达当前边界
                   end = maxPos;//新的边界
                   step++;  //再次起跳
               }
           }
        }
        return step;
    }
};